To Explain the World: The Discovery of Modern Science (39 page)

A warning: The reasoning in these notes is not necessarily identical to that followed historically. From Thales to Newton, the style of the mathematics that was applied to physical problems was far more geometric and less algebraic than is common today. To analyze these problems in this geometric style would be difficult for me and tedious for the reader. In these notes I will show how the results obtained by the natural philosophers of the past do follow (or in some cases, do not follow) from the observations and assumptions on which they relied, but without attempting faithfully to reproduce the details of their reasoning.

Notes

1.     Thales’ Theorem

2.     Platonic Solids

3.     Harmony

4.     The Pythagorean Theorem

5.     Irrational Numbers

6.     Terminal Velocity

7.     Falling Drops

8.     Reflection

9.     Floating and Submerged Bodies

10.   Areas of Circles

11.   Sizes and Distances of the Sun and Moon

12.   The Size of the Earth

13.   Epicycles for Inner and Outer Planets

14.   Lunar Parallax

15.   Sines and Chords

16.   Horizons

17.   Geometric Proof of the Mean Speed Theorem

18.   Ellipses

19.   Elongations and Orbits of the Inner Planets

20.   Diurnal Parallax

21.   The Equal-Area Rule, and the Equant

22.   Focal Length

23.   Telescopes

24.   Mountains on the Moon

25.   Gravitational Acceleration

26.   Parabolic Trajectories

27.   Tennis Ball Derivation of the Law of Refraction

28.   Least-Time Derivation of the Law of Refraction

29.   The Theory of the Rainbow

30.   Wave Theory Derivation of the Law of Refraction

31.   Measuring the Speed of Light

32.   Centripetal Acceleration

33.   Comparing the Moon with a Falling Body

34.   Conservation of Momentum

35.   Planetary Masses

1. Thales’ Theorem

Thales’ theorem uses simple geometric reasoning to derive a result about circles and triangles that is not immediately obvious. Whether or not Thales was the one who proved this result, it is useful to look at the theorem as an instance of the scope of Greek knowledge of geometry before the time of Euclid.

Consider any circle, and any diameter of it. Let
A
and
B
be the
points where the diameter intersects the circle. Draw lines from
A
and
B
to any other point
P
on the circle. The diameter and the lines running from
A
to
P
and from
B
to
P
form a triangle,
ABP.
(We identify triangles by listing their three corner points.) Thales’ Theorem tells us that this is a right triangle: the angle of triangle
ABP
at
P
is a right angle, or in other terms, 90°.

The trick in proving this theorem is to draw a line from the center
C
of the circle to point
P.
This divides triangle
ABP
into two triangles,
ACP
and
BCP.
(See Figure 1.) Both of these are isosceles triangles, that is, triangles with two sides equal. In triangle
ACP
, sides
CA
and
CP
are both radii of the circle, which have the same length according to the definition of a circle. (We label the sides of a triangle by the corner points they connect.) Likewise, in triangle
BCP
, sides
CB
and
CP
are equal. In an isosceles triangle the angles adjoining the two equal sides are equal, so angle
α
(alpha) at the intersection of sides
AP
and
AC
is equal to the angle at the intersection of sides
AP
and
CP
, while angle
β
(beta) at the intersection of sides
BP
and
BC
is equal to the angle at the intersection of sides
BP
and
CP.
The sum of the angles of any triangle is two right angles,
*
or in familiar terms 180°, so if we take
αʹ
as the third angle of triangle
ACP
, the angle at the intersection of sides
AC
and
CP
, and likewise take
βʹ
as the angle at the intersection of sides
BC
and
CP
, then

2
α
+
α
ʹ = 180°  2
β
+
β
ʹ = 180°

Adding these two equations and regrouping terms gives

2(
α
+
β
) + (
α
ʹ +
β
ʹ) = 360°

Now,
αʹ
+
βʹ
is the angle between
AC
and
BC
, which come together in a straight line, and is therefore half a full turn, or 180°, so

2(
α
+
β
) = 360° − 180° = 180°

and therefore
α
+
β
= 90°. But a glance at Figure 1 shows that
α
+
β
is the angle between sides
AP
and
BP
of triangle
ABP
, with which we started, so we see that this is indeed a right triangle, as was to be proved.

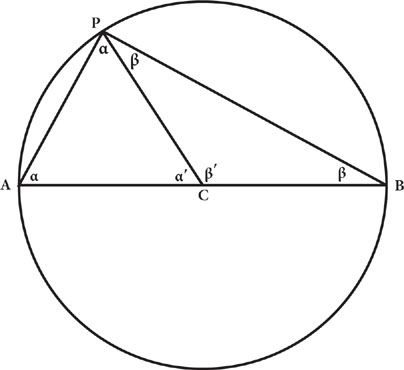
Figure 1. Proof of Thales’ theorem.
The theorem states that wherever point
P
is located on the circle, the angle between the lines from the ends of the diameter to
P
is a right angle.

2. Platonic Solids

In Plato’s speculations about the nature of matter, a central role was played by a class of solid shapes known as regular polyhedrons, which have come also to be known as Platonic solids. The regular polyhedrons can be regarded as three-dimensional generalizations of the regular polygons of plane geometry, and
are in a sense built up from regular polygons. A regular polygon is a plane figure bounded by some number
n
of straight lines, all of which are of the same length and meet at each of the
n
corners with the same angles. Examples are the equilateral triangle (a triangle with all sides equal) and the square. A regular polyhedron is a solid figure bounded by regular polygons, all of which are identical, with the same number
N
of polygons meeting with the same angles at every vertex.

The most familiar example of a regular polyhedron is the cube. A cube is bounded by six equal squares, with three squares meeting at each of its eight vertices. There is an even simpler regular polyhedron, the tetrahedron, a triangular pyramid bounded by four equal equilateral triangles, with three triangles meeting at each of the four vertices. (We will be concerned here only with polyhedrons that are convex, with every vertex pointed outward, as in the case of the cube and the tetrahedron.) As we read in the
Timaeus
, it had somehow became known to Plato that these regular polyhedrons come in only five possible shapes, which he took to be the shapes of the atoms of which all matter is composed. They are the tetrahedron, cube, octahedron, dodecahedron, and icosahedron, with 4, 6, 8, 12, and 20 faces, respectively.

The earliest attempt to prove that there are just five regular polyhedrons that has survived from antiquity is the climactic last paragraph of Euclid’s
Elements.
In Propositions 13 through 17 of Book XIII Euclid had given geometric constructions of the tetrahedron, octahedron, cube, icosahedron, and dodecahedron. Then he states,
*
“I say next that no other figure, besides the said five figures, can be constructed which is contained by equilateral and equiangular figures equal to one another.” In fact, what Euclid actually demonstrates after this statement is a weaker result, that there are only five combinations of the number
n
of sides of each polygonal face, and the number
N
of polygons meeting at each vertex, that are possible for a regular polyhedron. The proof
given below is essentially the same as Euclid’s, expressed in modern terms.

The first step is to calculate the interior angle
θ
(theta) at each of the
n
vertices of an
n
-sided regular polygon. Draw lines from the center of the polygon to the vertices on the boundary. This divides the interior of the polygon into
n
triangles. Since the sum of the angles of any triangle is 180°, and each of these triangles has two vertices with angles
θ
/2, the angle of the third vertex of each triangle (the one at the center of the polygon) must be 180° –
θ
. But these
n
angles must add up to 360°, so
n
(180° –
θ
) = 360°. The solution is

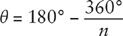
For instance, for an equilateral triangle we have
n
= 3, so
θ
= 180° – 120° = 60°, while for a square
n
= 4, so
θ
= 180° – 90° = 90°.

The next step is to imagine cutting all the edges and vertices of a regular polyhedron except at one vertex, and pushing the polyhedron down onto a plane at that vertex. The
N
polygons meeting at that vertex will then be lying in the plane, but there must be space left over or the
N
polygons would have formed a single face. So we must have
Nθ
< 360°. Using the above formula for
θ
and dividing both sides of the inequality by 360° then gives

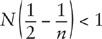
or equivalently (dividing both sides by
N
),

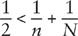
Now, we must have
n
≥ 3 because otherwise there would be no area between the sides of the polygons, and we must have
N
≥ 3 because otherwise there would be no space between the faces coming together at a vertex. (For instance, for a cube
n
= 4 because the sides are squares, and
N
= 3.) Thus the above inequality does not allow either 1/
n
or 1/
N
to be as small as 1/2 – 1/3 = 1/6,
and consequently neither
n
nor
N
can be as large as 6. We can easily check every pair of values of whole numbers 5 ≥
N
≥ 3 and 5 ≥
n
≥ 3 to see if they satisfy the inequality, and find that there are only five pairs that do: