Arrival of the Fittest: Solving Evolution's Greatest Puzzle (30 page)

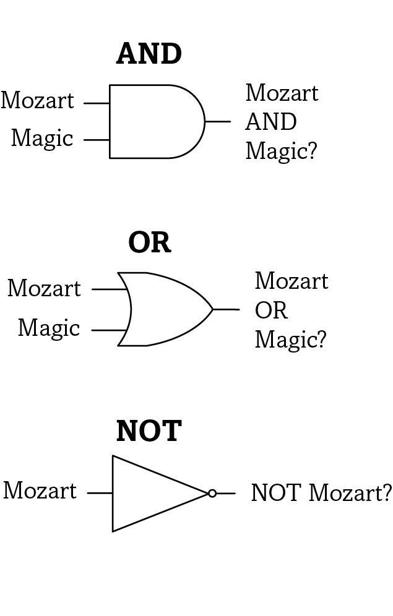
If you wanted to find compositions whose title contained the word “Mozart”
or
“magic” (
or
both), the search engine would have to compute another Boolean function: the OR function. Same input stream—everything with the word “Mozart” and “magic”—but a different rule. In this case, the output is a yes if at least one partial answer is a yes (figure 20b). As a result, the OR function would report not only
The Magic Flute
but also every other one of Mozart’s 626 pieces,
³⁹
as well as Santana’s “Black Magic Woman,” Stevie Wonder’s “If It’s Magic,” and hundreds more. An even simpler Boolean function, the NOT function (figure 20c) turns a yes into a no, and could help you find all compositions without the word “Mozart” in them.

These and other more exotic Boolean logic functions—XOR, XNOR, NAND, NOR—allow us to translate complex questions from natural languages into the strings of binary numbers that rule the world of computers. What’s more, binary numbers can encode any decimal number, and can be added, subtracted, multiplied, and divided just like decimal numbers. The integrated circuits of even the most sophisticated computers perform nothing but basic arithmetic and simpler Boolean logic functions like the AND function. With the simplest of all possible alphabets—zeroes and ones—and Boolean logic, digital computers can recognize images, encrypt information, deliver voice mail, and predict next Tuesday’s weather. Arithmetic, it turns out, is even more important than we learned in grade school.

Another remarkable fact about Boolean functions is that even the most complicated Boolean function can be computed by stringing together simpler functions, such that the output of one function becomes the input of another. It’s a bit like multiplication (3 × 4), which can be written as a series of additions (4 + 4 + 4). More than that, even though the number of possible Boolean functions is virtually infinite, each of them can be computed by stringing together only AND, OR, and NOT functions. This matters for computers, because in an integrated circuit, transistors are wired into units of computation that compute a simple Boolean function and that are known as
logic gates
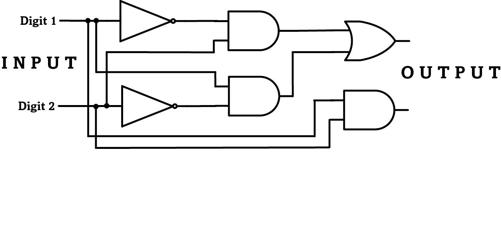
. Figure 21 shows some of the symbols that chip designers use for the simple AND, OR, and NOT gates. Each gate has one or two wires to the left for its input bits, and one on the right for its output bit. In figure 22 a few gates are wired to perform the simplest possible arithmetic operation of adding two binary digits—this already requires six logic gates, each with multiple transistors.
⁴⁰
Today’s chips of course add, subtract, multiply, and divide much longer numbers of sixty-four binary digits, and require millions of gates.
⁴¹

Most integrated circuits are hardwired in the factory, but robots like YaMoR are equipped with programmable hardware, chips that can be rewired to alter what some logic gates do—changing an AND gate into an OR gate, for example—and how these gates are wired. Some programmable chips can even be rewired while the chip is working.
⁴²
With more than a million logic gates, such chips are not just simple toys but powerful and flexible computing engines that could eventually help machines learn much as we do—by rewiring their own hardware—and create autonomous robots that can not just explore the world but also learn about its potholes and other pitfalls.
⁴³

If this sounds familiar, it’s because such learning resembles evolution, which alters life’s genotypes one molecule at a time. A programmable circuit’s logic gates and wiring are an analog of a genotype that can be altered to explore new computations, the analog of new phenotypes. Like evolution, the learning process requires plenty of trial and error. It reinforces good behavior, and punishes bad behavior. (But not as severely as evolution does. If your—or a future robot’s—golf game is weak, you may need to improve your stance, your grip, or your swing, but you need not die.) What is more, such learning need not destroy old knowledge. As you learn to play golf, you can still sit, walk, run, or jump, even though the neural circuit responsible for these skills gets rewired. And the parallels to evolution don’t end here. The wires connecting logic gates are generic links, just as flexible as the peptide bonds of proteins, because the output of any one gate can be fed into any other gate.
⁴⁴
As with proteins, such links can be built, destroyed, and modified without much ingenuity to create electronic circuits that can be wired in astronomically many ways.
⁴⁵

Standard links. Few kinds of logic gates. These principles already suffice to create chips that play chess more powerfully than mankind’s best, to find a single page in a million different books, or to “print” objects in three dimensions. The capabilities of real-world programmable circuits are so reminiscent of nature’s innovation powers that they suggest a profound question: Are entire libraries of digital circuits—huge circuit collections that can be created through recombining logic gates in every possible way—organized like the library of biological circuits? The answer can tell us whether the warp drives of biological innovation could be mounted on the spaceships of technological innovation.

Karthik Raman provided this answer. A graduate from the Indian Institute of Science, one of India’s top universities, Karthik came to my lab as a postdoctoral researcher. And he did not come alone. He also brought an effervescent enthusiasm for science, dogged tenacity in the face of failure—as inevitable in science as in evolution—and a wizardlike talent for analyzing complex data. When I invited him to map libraries of programmable circuits, he jumped right on it.

Although commercially available programmable chips have more than a million gates, some back-of-the envelope calculations convinced us that we should study smaller circuits. A library of circuits with a mere sixteen logic gates contains 10
⁴⁶
such circuits—a number already large beyond imagination—and this number increases exponentially with the number of gates, to 10
¹⁰⁰
circuits with only thirty-six gates.
⁴⁶
Huge numbers like this also made the decision of whether to build circuits in hardware or to study them in the computer easy: Millions of circuits are most easily analyzed inside a computer.
⁴⁷

A sixteen-gate circuit could in principle compute 10
¹⁹
—a million trillion—Boolean functions, but we didn’t know whether the library’s circuits encoded that many.
⁴⁸
Perhaps its circuits could compute only a few functions, like addition or multiplication. To find out, Karthik first cast a net wide enough to haul in as many volumes as possible from the circuit library. He created many circuits with random wirings, two million of them, and found that they computed more than 1.5 million logic functions, only a few of them as familiar as the AND function. Even though he had hauled in only a small fraction of circuits—there were still 10
⁴⁰
circuits left, and 10
¹²
times more functions to explore—his enormous catch taught us that even simple circuits can compute numerous Boolean functions.

Because the library hosts many more circuits than there are functions—10
²⁶
times more, to be precise—we knew that there must be multiple synonymous texts, circuits computing the same logic function, but we didn’t know how they were organized. To find out, Karthik started with a circuit that computed an arbitrary logic function and changed it to one of its neighbors in the library, for example by reconnecting the input of one gate to the input of another. If this “mutated” circuit still computed the same logic function, Karthik kept it. If not, he tried another rewiring, and repeated that until he had found a circuit with the same function. From that new circuit he took another step, and another, and so on, such that each step preserved the circuit’s function. Karthik started random walks like this from more than a thousand different circuits, each one computing a different function that needed to be preserved.

The networks of circuits he found reached even farther through the library than the genotype networks from earlier chapters: From most circuits one could walk
all the way
through the circuit library without changing a circuit’s logic function. Two circuits may share nothing, not a single gate or wire, except the logic function they express, yet they can still be part of a huge network of circuits connectable through many small wiring changes. What’s more, we found that this holds for every single function we studied. It is a fundamental property of digital logic circuits.
⁴⁹
The library of digital electronics is like biology, only more so.

Karthik next turned to the neighborhoods of different circuits computing the same function, created all their neighbors, and listed the logic functions that each of them computed. He found that these neighborhoods are just as diverse as those in biology. More than 80 percent of functions are found near one circuit but not the other.
⁵⁰
This is good news for the same reason as in biology: One can explore ever more logic functions while rewiring a circuit without changing its capabilities. A circuit’s neighborhood contains circuits with some sixty new functions, but a mere ten rewiring steps make a hundred new functions accessible, a hundred rewirings put four hundred new functions within reach, and a thousand changes can access almost two thousand new functions.
⁵¹

And the similarities continued. Earlier I mentioned the multidimensional fabric of biological innovability, the almost unimaginably complex, densely woven tissue of genotype networks. Karthik found that it has a counterpart in the circuit library, where a circuit with any function could be reached from any starting circuit by changing only a small percentage of wires. A fabric just like that of life’s innovability exists in digital electronics, and it can accelerate the search for a circuit best suited for any one task.
⁵²

Circuit networks thus have all it takes to become the warp drives of programmable hardware, in precisely the same way that genotype networks are the warp drives of evolution. They have the potential to help future generations of YaMoRs learn many new skills, from simple self-preservation like avoiding deadly staircases to complex skills like doing the dishes or playing ball with children. In this vision, their digital brains can rewire themselves step by little step, and explore many new behaviors, while being able to preserve old behavior—conserving the old while exploring the new.
⁵³
I wouldn’t even be surprised if our brains used a similar strategy to learn. We already know that they continually rewire the synaptic connections between our neurons, but perhaps our brains also explore new connections in the same way that organisms explore a genotype network. If so, the very same principle allowing biological innovation could be at work in the engines of human creativity.

Unfortunately, our ignorance in this area is still nearly absolute. We know next to nothing about the material basis of human creativity. We
do
know, however, that the kind of creativity we discovered is not free, because Karthik found its price tag
.
It was a familiar one.