Born on a Blue Day: Inside the Extraordinary Mind of an Autistic Savant (25 page)

Abstracts are handled in a number of ways in Mänti. One is to create a compound to describe it: ‘tardiness’ or ‘lateness’ is translated as
kellokült
(literally ‘clock-debt’). Another method is to use ‘word pairs’, as can be found in Finno-Ugrian languages such as Estonian. For a word such as ‘dairy (produce)’ the Mänti equivalent is
pîmat kermat
(‘milks creams’) and for ‘footwear’ it is
koet saapat
(‘shoes boots’).

Although Mänti is very different from English, there are quite a lot of words that are recognisable to English speakers:
nekka
(‘neck’),
kuppi
(‘cup’),
purssi
(‘wallet’),
nööt
(‘night’) and
pêpi
(‘baby’) are examples.

Mänti exists as a tangible, communicable expression of my inner world. Each word, shining with colour and texture, to me is like a piece of art. When I think or speak in Mänti, I feel as though I am painting in words.

10

A Very Large Slice of Pi

I first learned about the number pi in my maths class at school. Pi – the ratio of a circle’s circumference to its diameter – is mathematics’ most celebrated number; the name comes from the sixteenth letter of the Greek alphabet (π), the symbol being adopted by the mathematician Euler in 1737. I was immediately fascinated by it and learned as many of its decimal digits as I could find from various library books, hundreds of them in total. Then, in late 2003, I received a phone call from my father who reminded me at the end of the conversation that it had been twenty years since my early childhood seizures. He said that I should be proud of the progress I had made in the time since. I thought about what he said for a long time afterwards and decided that I wanted to do something to show that my childhood experience of epilepsy had not held me back. Later that week I contacted the fundraising department of the National Society for Epilepsy, the largest epilepsy charity organisation in the UK. To help raise funds for the NSE, my plan was to learn as many digits of the number pi as I could in correct sequence, before a public recitation in three months’ time, on 14 March – International Pi Day (14 March is 3/14 in US notation) – which is also Einstein’s birthday. The charity was excited by the idea and suggested that I attempt to break the European record, so a target of 22,500 digits was set. While I began learning the numbers, the charity’s fundraising manager Simon Ekless organised the setting for the recitation, the Ashmolean Building at the Museum of the History of Science in Oxford, where among the various exhibits is one of Albert Einstein’s blackboards.

Pi is an irrational number, which means that it cannot be written as a simple fraction of two whole numbers. It is also infinite: the digits to the right of the decimal point go on forever in a never-ending numerical stream, so that it isn’t possible for someone to write down the number pi exactly, even if he or she had a piece of paper as big as the universe to write it on. For this reason, calculations must always use approximations of pi, such as 22 ÷ 7 or 355 ÷ 113. The number appears in all sorts of unexpected places in mathematics besides circles and spheres. For example, it occurs in the distribution of primes and in the probability that a pin dropped on a set of parallel lines will intersect a line. Pi also appears as the average ratio of the actual length and the direct distance between source and mouth in a meandering river.

The earliest values of pi were almost certainly found by measurement. There is good evidence that the ancient Egyptians had 4(8/9)
²
= 3.16 as a value for pi, while the Babylonians used the approximation 3 + 1/8 = 3.125. The Greek mathematician Archimedes of Syracuse gave the first theoretical calculation for the value of pi in around 250
BC
. He determined the upper and lower range of pi by finding the perimeters of a polygon inscribed within a circle, which is less than the circumference of a circle (Fig.1) and of a polygon circumscribed outside a circle, which is greater than the circumference (Fig.2).

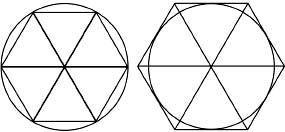
By doubling the number of sides of the hexagon to a dodecagon (twelve sides), then a twenty-four and forty-eight-sided polygon, and finally up to a ninety-six-sided polygon, Archimedes brought the two perimeters closer and closer in length to the circle’s circumference, thereby arriving at his approximation. He calculated that pi was less than 3 1/7 but greater than 3 10/71. This translates in decimal notation to between 3.1408 and 3.1429 (rounded up to four decimal places), which is very close to the actual value of 3.1416.

During the Middle Ages, the German mathematician Ludolph van Ceulen spent a large part of his life calculating the numerical value of pi, using essentially the same methods as the ones employed by Archimedes some 1800 years before. In 1596, he gave a value of pi to 20 decimal places in his book
Van den Circkel
(
On the Circle
), which he later expanded to 35 decimals. After his death, the digits were engraved on his tombstone.

Later mathematicians, including Isaac Newton and James Gregory, developed new arithmetical formulas to improve their calculations of the value of pi. In 1873, the Englishman William Shanks published his calculation of pi to 707 decimal places. It had taken him more than fifteen years, averaging about one decimal a week. Unfortunately, in the 1940s, when checked using mechanical calculators, it was discovered that he had made an error in the 528th place, after which all his subsequent digits were wrong.

With the advent of modern computers, it became possible to calculate pi to much greater values than ever before. The first computer calculation of pi was performed in 1949 on ENIAC (Electronic Numerical Integrator and Computer) – a huge machine that weighed 30 tons and was the size of a small house – calculating to 2,037 decimal places in seventy hours. Since then, rapid improvements in computer technology have helped researchers compute pi to an ever-increasing number of digits. In 2002, computer scientist Yasumasa Kanada and his coworkers at the University of Tokyo Information Technology Centre computed pi to more than one trillion decimal places.

Over the years, many pi enthusiasts have attempted to memorise some of the number’s infinite string of digits. The most common method uses sentences and even whole poems composed of carefully chosen words, with the number of letters in each representing successive digits of pi. Perhaps the most famous example is the following, attributed to the British mathematician Sir James Jeans:

How I want a drink, alcoholic of course, after the heavy lectures involving quantum mechanics!

Where the word ‘How’ = 3 (having three letters) and ‘I’ 1 and ‘want’ 4, the complete sentence translating to 3.14159265358979, which is pi to 14 decimal places.

Another (first published in 1905) gives pi to 30 decimal places:

Sir, I send a rhyme excelling

In sacred truth and rigid spelling

Numerical sprites elucidate

For me the lexicon’s dull weight

If Nature gain

Not you complain,

Tho’ Dr Johnson fulminate.

A challenge such writers face is how to deal with the digit 0, which first occurs in the thirty-second place after the decimal point. One solution is to use punctuation, a full stop for example. Another is to use a ten-letter word. Some writers use longer words for two successive digits. For example, the eleven-letter word ‘calculating’ would stand for a 1 followed by another 1.

When I look at a sequence of numbers, my head begins to fill with colours, shapes and textures that knit together spontaneously to form a visual landscape. These are always very beautiful to me; as a child I often spent hours at a time exploring numerical landscapes in my mind. To recall each digit, I simply retrace the different shapes and textures in my head and read the numbers out of them.

For very long numbers, such as pi, I break the digits down into smaller segments. The size of each segment varies, depending on what the digits are. For example, if a number is very bright in my head and the next one is very dark, I would visualise them separately, whereas a smooth number followed by another smooth number would be remembered together. As the sequence of digits grows, my numerical landscapes become more complex and layered, until – as with pi – they are like an entire country in my mind, composed of numbers.

This is how I ‘see’ the first twenty digits of pi:

The number slopes upwards, then darkens and becomes bumpy in the middle before curving and meandering down.

And here are the first 100 digits of pi as I see them:

At the end of each segment of numbers, the landscape changes and new shapes, colours and textures appear. This process continues on and on, for as long as the sequence of digits that I am recalling.

The most famous sequence of numbers in pi is the ‘Feynman point’, which comprises the 762nd through 767th decimal places of pi: ‘… 999999 …’. It is named after the physicist Richard Feynman for his remark that he would like to memorise the digits of pi as far as that point so that when reciting them, he would be able to finish with: ‘… nine, nine, nine, nine, nine, nine, and so on.’ The Feynman point is visually very beautiful to me; I see it as a deep, thick rim of dark blue light.

There is a similarly beautiful sequence of digits comprising the 19,437th through 19,453rd decimal places of pi: ‘… 99992128599999399 …’, where the digit nine first repeats four times in a row, then very shortly afterwards five times over and then twice more again; eleven times altogether in the space of 17 decimal places. It is my favourite sequence of pi’s digits in all the more than 22,500 that I learned.

I began studying pi in December 2003, having three months to learn all the digits (22,500+) needed to attempt the record. The first problem was where to find so many digits of pi: most books only gave the number to some tens or hundreds of places. The Internet proved to be the answer, though even then it took a lot of searching as most websites only listed pi to a thousand or several thousand places. Finally, Neil found the website of a Tokyo-based supercomputer which had files that stored millions of pi’s digits. This, then, became our source for the record attempt.