E=mc2 (30 page)
Authors: David Bodanis
By August, [U.S. bombers] had burned out fifty-eight [Japanese cities]: The gasoline and napalm that American fliers poured onto Japanese cities didn't have enough energy to achieve such destruction. The real source was the thermonuclear radiation of the sun. That radiation beamed down to Earth, and accumulated over years in the chemical bonds within trees. The Japanese themselves had collected that energy—in the lumber with which their cities were largely built. What the American firebombs did was briefly lower the barriers keeping that originally thermonuclear— and now chemical—energy inside. In other words, once sufficient ignition had been created, the firestorms powered themselves.
"I told him I was against it on two counts . . .": Harold Evans,
The American Century
(London: Jonathan Cape, 1998), p. 325.
Notes from the Presidential Interim Committee . . . : Richard Rhodes,
Making of the Atomic Bomb
(New York: Simon & Schuster, 1986), pp. 650-51. Further detailed minutes of the meeting are available in Martin J. Sherwin's
A World Destroyed: The Atomic Bomb and the Grand Alliance
(New York: Knopf, 1975), see especially pp. 302-3.
The army built weapons to use them: Scientists in many countries have similar memories about being abruptly reminded where they came in the chain of command. Andrei Sakharov—a great physicist before he became a dissident—described the evening after the Soviet Union's powerful thermonuclear test of 1955. Marshal Nedelin gave a banquet that night for all the top staff involved. And Sakharov, recalling the spreading fireball he'd seen, gave a toast:
"I said something like: 'May all our devices explode as successfully as today's, but always over test sites and never over cities.' The table fell silent, as if I had said something indecent. Nedelin grinned a bit crookedly. Then he rose, glass in hand, and said: 'Let me tell a parable. An old man wearing only a shirt was praying before an icon. "Guide me, harden me. Guide me, harden me.
"
His wife, who was lying on the stove said: "Just pray to be hard, old man, I can guide it in myself." Let's drink to getting hard.'
'My whole body tensed, and I think I turned pale . . . I drank my brandy in silence . . . Many years have passed, but I still feel as if I had been lashed by a whip
. . . " Andrei Sakharov, in
Memoirs,
trans. Richard Laurie (London: Hutchinson, 1990),
p. 194.
13. 8:16 A.M.—Over Japan
"an elongated trash can with fins": The main sources for the account in this chapter are Rhodes,
The Making of the Atomic Bomb,
pp. 701-15; Robert Serber,
The Los Alamos Primer
(Berkeley: University of California Press, 1992), especially pp. 35-49; as well as standard textbook physics. The "trash can" observation was made by Jacob Beser, one of the plane's crew members; in Rhodes, p. 701.
At just under 2,000 feet the height would be ideal: There is a great hardening of attitudes in wartime. In the memo which Frisch and Peierls wrote in March 1940, detailing the theoretical possibility of a practical atomic bomb, they observed:
Owing to the spread of radioactive substances with the wind, the bomb could probably not be used without killing large numbers of civilians, and this may make it unsuitable as a weapon for use by this country. (Use as a depth charge near a naval base suggests itself but even there it is likely that it would cause great loss of civilian life by flooding and by the radioactive radiations.)
The point is not that dropping the bomb was necessarily wrong: rather, five years after this civilized memo, altitudes for optimal blast yield over a mostly civilian center had become part of ordinary work. For a full copy of what Frisch and Peierls wrote—and what Briggs locked in the safe—see Rudolf Peierls,
Atomic Histories
(New York: Springer-Verlag, 1997), pp. 187-94. On the way that democracies, especially, are liable to experience such chilling transformations, there are Tocqueville's famous 1830s comments on the careerist factors involved
(Democracy in America,
vol. 1, part 3, chapter 24), while Victor Davis Hanson goes much deeper in his first-rate
The Soul of Battle
(New York: The Free Press, 1999).
. . . the ordinary electricity of the protons was available . . . : The power is so great that it's often thought nuclear explosions are produced by some new form of energy, which had never existed before. But that's not so. Atomic bombs simply explode because of static electricity.
Electrical repulsion depends very much on the distance between objects. Hold your finger far from a metal surface on a dry winter day and the force between them won't be enough to break down the resistance of the air between them. But let your finger dangle closer—lowering the distance between them—and the overall force gets bigger, until ZAP!! You get struck by the power of static electricity.
A nucleus is about 1,000 times narrower than a whole atom. This means that each of the charged particles crammed in the nucleus will push apart with about 1,000 times greater force than we're used to from the ordinary pushing apart of more widely spaced surface electrons. (The details are slightly different from this, but the results are similar.)
At the same time, instead of just one charged particle pushing against a single other charged particle—as with two electrons pushing apart—the nucleus of a uranium atom contains 92 charged particles. Normally they're held together by the strong nuclear force, but if that's overcome suddenly, its as if there were 92 charged particles hovering right next to each other, with nothing but crackling electrical repulsion acting between them. Now, when one electron is held near one other electron and starts pushing apart, the energy due to their charge is 1 X 1. When there are
92
protons, this part of their opposing energy is 92 X 92, which is over 8,400.
In an atomic bomb, both effects are operating at once. The charged particles in the uranium nucleus push outward about 1,000 times more than in ordinary sparks or chemical explosions, from having been crammed into the small nucleus. That gets multiplied a further 8,400 or so times from the charge of the dense, proton-packed nucleus. The total energy forcing itself outward is then on the order of 1,000 X 8,400, or more than 8 million times greater than the ordinary electrical forces we're used to, be it the resistance of a wooden bat against a pitched ball or the wild roar of a rocket's chemical fuel exploding. A full calculation requires more adjustments, but the overall proportions are accurate enough. It might sound like hyperbole to say that an atomic bomb is millions of times more powerful than any previous explosive—but it's true.
Mass was . . . coming out as the energy of speeding nuclei fragments: (This and a few of the next entries show how E=mc
2
enters into practical atomic engineering and astrophysics.) Most of the exploding uranium over Hiroshima remained as a dispersed haze, and only about one percent of each exploding atom got transformed. It doesn't seem much, for if one takes the mass of a single uranium atom, multiplies it by c
2
(E=mXc
2
), and then divides by 100 (to take into account this fact that only 1 percent of it "exploded"), the figure that results is a mere 2.7 X 10
-6
ergs. That's far too little energy to even blow out a candle, but there were well over 100,000,000,000,000,000,000,000 uranium atoms laboriously concentrated by American technicians in the Hiroshima bomb. Those combined microbursts were what killed so many people, shattering so many buildings and roads.
[the uranium fragments] soon were . . . traveling at a substantial fraction of the speed of light: In the entry on Newton for Chapter 7, we saw how the power of equations allows a researcher to know the strength of our planet's gravity at the distant orbit of the moon, without ever having to leave a book-lined study on Earth. In the same way, it really is possible to look inside an exploding atomic bomb, and accurately compute the speed of the roaring shattered fragments. The equation that allows this, in part, is none other than the old kinetic energy formula from Leibniz and Emilie du Châtelet.
By their work, the kinetic energy of the speeding fragments is = ½mv
2
, where "m" is the mass of the exploding nuclei, and "v" is the speed at which they hurtle apart. If you know that E=½mv
2
, then you can multiply by 2 to get 2E = mv
2
, and then divide by m to get 2E/m = v
2
, and finally take the square root, to end up with the expression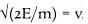
. Plug in the right values for "E" and "m," and you'll be able to look inside an exploding atomic bomb, and compute the speed
of
the escaping fragments.
We know the values for the energy "E" of a single exploding uranium atom: it's 2.7 X 10
-6
ergs. Insert that in the formula
(2E/m), and the result is that each flung-out fragment of the bomb's core is traveling at the speed of v=1.2 X 10
8
cm/sec. (Again there are modifications, but the overall reasoning holds.) That's over 2 million miles per hour—which is why the solid block of uranium inside the bomb will very quickly become a sphere of hotter-than-boiling gas, racing outward at this extremely high rate.
It's an important result, for the neutrons that are still emerging from the fissioning nuclei will only be able to work if they can catch up with these escaping fragments. That's the reason slow neutrons, of the sort Fermi first analyzed— and which are
so
useful in gradually cooking up plutonium—are not of any use once a blast finally begins. To keep an explosion
going, the
bomb has to be constructed so that the shattered fragments release neutrons that travel faster than the escaping cloud of liquefied and then gaseous uranium. Instead of 3 million mph, they have to emerge at 30 million mph or more—and this is what was happening inside the bomb over Hiroshima.
This is also why commercial reactors can't explode like a full-sized atomic bomb: the slow neutrons they operate with wouldn't be able to catch up with an initial explosion; the chain reaction would stop, and the explosion would fizzle out. In that sense, commercial reactors are intrinsically safe. (Again, though, "safe" is a relative term. Even an incomplete explosion can still tear a generator apart with a mighty bang: the roof of the Chernobyl containment vessel weighed many tons, but was flicked aside like balsa wood when the fuel underneath it overheated.)
The kinetic energy calculation is from Serber's
The Los Alamos Primer,
pp. 10 and 12; points on fast neutrons are succinctly presented in Bernstein's
Hitler's Uranium Club,
pp. 21-22.
. . . for a brief period . . . conditions similar to those in the early moments of the formation of the universe . . . : Could it have ignited the atmosphere? No, for the heat—though immense—was still not enough to cross the barriers for fusion to start. The only possible candidate for ignition would be the nitrogen that dominates the Earth's atmosphere. But long before the temperatures fusion would require could be reached, electrons would radiate away their energy so quickly that the necessary localized heat could never build up. The popular story that such an ignition might occur seems to have stemmed from a misunderstanding in a 1958 interview of one of the chief administrators by the novelist Pearl Buck. An excellent nontechnical summary of the physics is in Hans Bethe's
The Road From Los Alamos
(New York: Simon & Schuster, 1991), pp. 30-33.
. . . E=mc
2
'
s first work on planet Earth was done: There's a famous cover from
Time magazine,
showing a saddened Einstein with a mushroom cloud in the background, and the equation E=mc
2
appearing with Biblical authority on the clouds. The causality of Einstein's "responsibility," however, is more subtle. What happened over Hiroshima accurately followed the equation Einstein had written years before, but the equation was not sufficient for the detailed engineering involved; it was, in a sense, not even "necessary," as nuclear physicists could, in principle, have developed the needed technical expertise without any awareness that the overall pattern being summarized by the equation was taking place.