How to Pass Numerical Reasoning (30 page)
Read How to Pass Numerical Reasoning Online
Authors: Heidi Smith

Worked example
The average price of a London flat in 1970 was £40,000. By the end of the 1980s, the price had risen by 85%. By January 1992, house prices fell dramatically and the price of the same London flat, now beset with structural problems, fell by 40% on the December 1989 price. At how much more or less is the flat valued in 1992 than in 1970?
You are asked to find a new value following a percentage increase and then a percentage decrease. Increase the original whole (£40,000) by 85% (1 + 0.85) to find the December 1989 value: 40,000 × 1.85 = £74,000
New whole = £74,000
Decrease the new whole (£74,000) by 40% (1 – 0.4) to find the January 1992 value:
£74,000 | × | (1 – 0.4) | = | |
£74,000 | × | 0.6 | = | £44,400 |
The flat is worth £4,400 more in 1992 than the 1970 value.
Percentage increase and decrease practice questions
Q1
Increase 25% of 18 by 15% of 60.
Q2
What is the percentage profit a secondhand car dealer makes on a car he buys for £2,400 and sells for £3,200?
Q3
The share price for stock S rose by 20% on the first day of trading. In the first few minutes of trading the next day, the stock rose by a further 2.5%. By what percentage has the stock gained in price?
Q4
An apple tree grows by 5% every year. When it is planted, its height is 90 cm. In which year will the tree exceed 1m in height?
Q5
Between 2000 and 2001, Kinji’s salary increased from £25,000 to £26,500. His projected salary increase for 2002 is 0.5% higher than the increase he received in 2001. What is Kinji’s projected salary for 2002?
Q6
If P is discounted by 25%, the new price of P is 12.5% of Q. What is P in terms of Q?
Q7
A child’s bike goes on sale at a 15% discount at the end of the summer holidays. By the October half-term holiday, the bike is marked down by a further 20% on the discounted price. If the original price of the bike was £125, what is the selling price of the bike after the October markdown?
Q8
A washing machine goes on sale for £289, which is a 66
2
⁄
3
% markdown on the original price. What was the original price?
Q9
A publisher sells a puzzle book to wholesalers for £6 for the first 21 books purchased and applies a 4% discount to each book purchased thereafter. If the wholesaler buys 30 puzzle books from the publisher, how much does the wholesaler save on the retail price of the order, if the retail price of the book is £7.99?
Q10
The distance between Lovetts Bay and Noe Valley is 124 miles and a car uses 25 litres of petrol to make the journey. After the engine has been tuned, fuel consumption is reduced by 2%. How much petrol is required for a round trip?
Simple interest and compound interest
Simple interest
is the amount of interest earned on an investment.
Compound interest
is the amount of interest earned on an investment plus interest earned on previously earned interest. A question that requires you to calculate interest is designed to test your ability to decide whether to perform a simple percentage change calculation or to combine cumulative percentage changes. The clue will usually be hidden in the question, so take your cue from the question itself, before performing any calculations.
Simple interest
To find simple interest, multiply the
principal sum
(usually the original amount invested) by the
interest rate
by the
time period
(usually expressed in years): Interest = Principal sum × Interest rate × Time period
Worked example
If Alex takes out a two-year loan of £2,000 from a bank, and pays simple annual interest of 8.75%, how much interest will he have paid by the end of the term? To work out how much interest is paid in one year, multiply £2000 (the principal sum) by the decimal equivalent of 8.75%: £2000 × 0.0875 = £175
In one year, £175 will be paid in interest. In two years, £175 × 2 will be paid (£350). Use the formula and plug in the numbers to verify your answer:
Principal sum | × | Interest rate | × | Time period | = | Interest |
£2000 | × | 0.0875 | × | 2 | = | £350 |
If the question asked you what is the total amount in the account at the end of the period, you would multiply by (1 + 0.0875). This is very important in compound interest calculations. For example:
Principal sum | × | (1 + Interest rate) | × | Time period | = | Interest plus |
£2000 | × | (1 + 0.0875) | × | 2 | = | £2,350 |
Compound interest
To find the compound interest payable on a principal sum, work out the interest on the principal sum for every year interest is accumulated. In compound interest, the charge is calculated on the sum loaned plus any interest accrued in previous periods.
The formula to find compound interest is I = P (1 + R)
n–1
where P = the principal sum, R = the rate of interest and n = the number of periods for which interest is calculated.
Worked example
Shifty borrows £500 over 2 years from a building society at a rate of 12% per annum compounded quarterly. How much interest will Shifty have to pay at the end of the 2-year loan?
Recall the formula to find compound interest: I = P (1 + R)
n–1
.
If £500 is loaned for 2 years at a rate of 12% per annum, compounded quarterly, the calculations need to be made on a quarterly basis. So the value of n will be 4 (quarters) × 2 (years) = 8, and the value of r will be
12
⁄
4
= 3% (per quarter). Therefore I = 500
(1.03)8–1
= £133.38.
Simple and compound interest practice questions
Q1
Jo invests £9,750 in an online savings account for 1 year and 6 months. Simple interest is paid at a rate of 3.75% per year and is calculated on a daily basis. To the nearest penny, how much is in the account at the end of the term?
Q2
Justin has £2,100 in his savings account. He deposited £1,500 two years ago. What is the simple annual interest rate on the account?
Q3
Katie invested £60 in a bond which yields a simple annual interest rate of 1.25%. If the total amount payable to Katie at the end of the term is £63.75, after how many years has Katie redeemed the bond?
Q4
Max bought a house for £40,000. The value of his house increased over 6 years, so that by the end of the term it had seen a 40% increase on the original price. The same amount invested in a bank account yields 9% per annum simple interest over the same period. Which is the more profitable investment option?
Q5
If Paul invests £385 in National Savings Certificates, which currently yield annual compound interest of 2.8%, what will his certificates be worth at the end of 3 years (to the nearest penny?)
Answers to Chapter 4
Percentage converter drill
Convert to percentage | Convert to decimal | Convert to fraction | |
Q1 | 0.25 = 25% | 1 | 87.5% = |
Q2 | 0.75 = 75% | 1 | 0.5% = |
Q3 | 0.1 = 10% | 5 | 0.125% = |
Q4 | 0.0047 = 0.47% | 3 | 60% = |
Q5 | 0.063 = 6.3% | 3 | 250% = 2½ |
Q6 | ½ = 50% | 0.1% = 0.001 | 0.625 = |
Q7 | 7 | 0.043% = 0.00043 | 2.75 = 2¾ |
Q8 | 5 | 8.3% = 0.083 | 0.006 = |
Q9 | 1 | 430% = 4.3 | 0.125 = |
Q10 | 4 | 5 | 6.002 = 6 |
Percentage formulae practice questions: explanations
In the following explanations, only one method is given. You may prefer to use another method to check your answers.
Q1
Answer
= 18
Convert 50% to its decimal equivalent and multiply the whole number by the decimal:
50% = 0.5
0.5 × 36 = 18
Q2
Answer
= 120
Convert 75% to its decimal equivalent and multiply the whole number by the decimal:
75% = 0.75
0.75 × 160 = 120
Q3
Answer
= 39
To find 10% of 130, move the decimal place one place to the left of the whole number:
10% = 13
30% = 3 × 10% = 39
Q4
Answer
= 5.76
24% is approximately equal to ¼ (25%) so your answer will be approximately ¼ × 24 = 6. Express the percentage as a fraction over 100 and multiply by the whole number (24):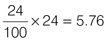
Q5
Answer
= 2