Hyperspace (21 page)

This was the missing piece in the puzzle. The secret of wood that bound matter together was the Yang-Mills field, not the geometry of Einstein. It appeared as though this, and not geometry, was the central lesson of physics.

Today, the Yang-Mills field has made possible a comprehensive theory of all matter. In fact, we are so confident of this theory that we blandly call it the
Standard Model
.

The Standard Model can explain every piece of experimental data concerning subatomic particles, up to about 1 trillion electron volts in energy (the energy created by accelerating an electron by 1 trillion volts). This is about the limit of the atom smashers currently on line. Consequently, it is no exaggeration to state that the Standard Model is the most successful theory in the history of science.

According to the Standard Model, each of the forces binding the various particles is created by exchanging different kinds of quanta. Let us now discuss each force separately, and then assemble them into the Standard Model.

The Standard Model states that the protons, neutrons, and other heavy particles are not fundamental particles at all, but consist of some even tinier particles, called
quarks
. These quarks, in turn, come in a wide
variety: three “colors” and six “flavors.” (These names have nothing to do with actual colors and flavors.) There are also the antimatter counterparts of the quarks, called antiquarks. (Antimatter is identical to matter in all respects, except that the charges are reversed and it annihilates on contact with ordinary matter.) This gives us a total of 3 × 6 × 2 = 36 quarks.

The quarks, in turn, are held together by the exchange of small packets of energy, called
gluons
. Mathematically, these gluons are described by the Yang-Mills field, which “condenses” into a sticky, taffylike substance that “glues” the quarks permanently together. The gluon field is so powerful and binds the quarks so tightly together that the quarks can never be torn away from one another. This is called
quark confinement
, and may explain why free quarks have never been seen experimentally.

For example, the proton and neutron can be compared to three steel balls (quarks) held together by a Y-shaped string (gluon) in the shape of a bola. Other strongly interacting particles, such as the π meson, can be compared to a quark and an antiquark held together by a single string (
Figure 5.3
).

Obviously, by kicking this arrangement of steel balls, we can set this contraption vibrating. In the quantum world, only a discrete set of vibrations is allowed. Each vibration of this set of steel balls or quarks corresponds to a different type of subatomic particle. Thus this simple (but powerful) picture explains the fact that there are an infinite number of strongly interacting particles. This part of the Standard Model describing the strong force is called quantum chromodynamics (QCD)—that is, the quantum theory of the color force.

In the Standard Model, the weak force governs the properties of “leptons,” such as the electron, the muon, and the tau meson, and their neutrino partners. Like the other forces, the leptons interact by exchanging quanta, called
W
and
Z
bosons. These quanta are also described mathematically by the Yang-Mills field. Unlike the gluon force, the force generated by exchanging the Wand Zbosons is too weak to bind the leptons into a resonance, so we do not see an infinite number of leptons emerging from our atom smashers.

The Standard Model includes the theory of Maxwell interacting with the other particles. This part of the Standard Model governing the interaction of electrons and light is called quantum electrodynamics (QED), which has been experimentally verified to be correct to within one part in 10 million, technically making it the most accurate theory in history.

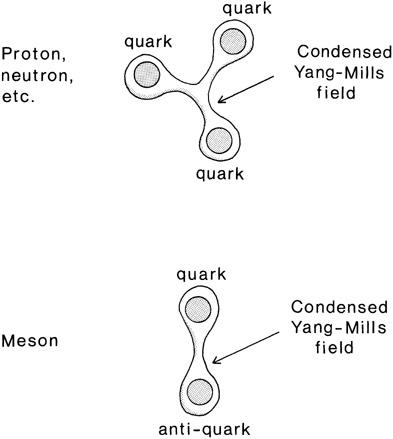
Figure 5.3. Strongly interacting particles are actually composites of even smaller particles, called quarks, which are bound together by a taffylike “glue,” which is described by the Yang-Mills field. The proton and neutron are each made up of three quarks, while mesons are made up of a quark and an antiquark
.

In sum, the fruition of 50 years of research, and several hundred million dollars in government funds, has given us the following picture of subatomic matter:
All matter consists of quarks and leptons, which interact by exchanging different types of quanta, described by the Maxwell and Yang—Mills
fields
. In one sentence, we have captured the essence of the past century of frustrating investigation into the subatomic realm. From this simple picture one can derive, from pure mathematics alone, all the myriad and baffling properties of matter. (Although it all seems so easy now, Nobel laureate Steven Weinberg, one of the creators of the Standard Model, once reflected on how tortuous the 50-year journey to discover the model had been. He wrote, “There’s a long tradition of theoretical physics, which by no means affected everyone but certainly affected me, that said the strong interactions [were] too complicated for the human mind.”
⁴
)

The details of the Standard Model are actually rather boring and unimportant. The most interesting feature of the Standard Model is that it is based on symmetry. What has propelled this investigation into matter (wood) is that we can see the unmistakable sign of symmetry within each of these interactions. Quarks and leptons are not random, but occur in definite patterns in the Standard Model.

Symmetry, of course, is not strictly the province of physicists. Artists, writers, poets, and mathematicians have long admired the beauty that is to be found in symmetry. To the poet William Blake, symmetry possessed mystical, even fearful qualities, as expressed in the poem “Tyger! Tyger! burning bright”:

Tyger! Tyger! burning bright
In the forests of the night
What immortal hand or eye
Could frame thy fearful symmetry?
⁵

To mathematician Lewis Carroll, symmetry represented a familiar, almost playful concept. In the “The Hunting of the Snark,” he captured the essence of symmetry when he wrote:

You boil it in sawdust:
You salt it in glue:
You condense it with locusts in tape:
Still keeping one principal object in view—
To preserve its symmetrical shape.

In other words, symmetry is the preservation of the shape of an object even after we deform or rotate it. Several kinds of symmetries occur repeatedly in nature. The first is the symmetry of rotations and reflections. For example, a snowflake remains the same if we rotate it by 60 degrees. The symmetry of a kaleidoscope, a flower, or a starfish is of this type. We call these space-time symmetries, which are created by rotating the object through a dimension of space or time. The symmetry of special relativity is of this type, since it describes rotations between space and time.

Another type of symmetry is created by reshuffling a series of objects. Think of a shell game, where a huckster shuffles three shells with a pea hidden beneath one of them. What makes the game difficult is that there are many ways in which the shells can be arranged. In fact, there are six different ways in which three shells can be shuffled. Since the pea is hidden, these six configurations are identical to the observer. Mathematicians like to give names to these various symmetries. The name for the symmetries of a shell game is called S
₃
, which describes the number of ways that three identical objects may be interchanged.

If we replace the shells with quarks, then the equations of particle physics must remain the same if we shuffle the quarks among themselves. If we shuffle three colored quarks and the equations remain the same, then we say that the equations possess something called SU(3) symmetry. The 3 represents the fact that we have three types of colors, and the SU stands for a specific mathematical property of the symmetry.
^*
We say that there are three quarks in a
multiplet
. The quarks in a multiplet can be shuffled among one another without changing the physics of the theory.

Similarly, the weak force governs the properties of two particles, the electron and the neutrino. The symmetry that interchanges these particles, yet leaves the equation the same, is called SU(2). This means that a multiplet of the weak force contains an electron and a neutrino, which can be rotated into each other. Finally, the electromagnetic force has U(l) symmetry, which rotates the components of the Maxwell field into itself.

Each of these symmetries is simple and elegant. However, the most controversial aspect of the Standard Model is that it “unifies” the three fundamental forces by simply splicing all three theories into one large symmetry, SU(3) × SU(2) × U(1), which is just the product of the
symmetries of the individual forces. (This can be compared to assembling a jigsaw puzzle. If we have three jigsaw pieces that don’t quite fit, we can always take Scotch tape and splice them together by hand. This is how the Standard Model is formed, by taping three distinct multiplets together. This may not be aesthetically pleasing, but at least the three jigsaw puzzles now hang together by tape.)

Ideally, one might have expected that “the ultimate theory” would have all the particles inside just a single multiplet. Unfortunately, the Standard Model has three distinct multiplets, which cannot be rotated among one another.

Promoters of the Standard Model can say truthfully that it fits all known experimental data. They can correctly point out that there are no experimental results that contradict the Standard Model. Nonetheless, nobody, not even its most fervent advocates, believes it is the final theory of matter. There are several deep reasons why it cannot be the final theory.

First, the Standard Model does not describe gravity, so it is necessarily incomplete. When attempts are made to splice Einstein’s theory with the Standard Model, the resulting theory gives nonsensical answers. When we calculate, say, the probability of an electron being deflected by a gravitational field, the hybrid theory gives us an infinite probability, which makes no sense. Physicists say that quantum gravity is
nonrenormalizable
, meaning that it cannot yield sensible, finite numbers to describe simple physical processes.

Second, and perhaps most important, it is very ugly because it crudely splices three very different interactions together. Personally, I think that the Standard Model can be compared to crossing three entirely dissimilar types of animals, such as a mule, an elephant, and a whale. In fact, it is so ugly and contrived that even its creators are a bit embarrassed. They are the first to apologize for its shortcomings and admit that it cannot be the final theory.

This ugliness is obvious when we write down the details of the quarks and leptons. To describe how ugly the theory is, let us list the various particles and forces within the Standard Model:

1. Thirty-six quarks, coming in six “flavors” and three “colors,” and their antimatter counterparts to describe the strong interactions

2. Eight Yang-Mills fields to describe the gluons, which bind the quarks

3. Four Yang-Mills fields to describe the weak and electromagnetic forces

4. Six types of leptons to describe the weak interactions (including the electron, muon, tau lepton, and their respective neutrino counterparts)

5. A large number of mysterious “Higgs” particles necessary to fudge the masses and the constants describing the particles

6. At least 19 arbitrary constants that describe the masses of the particles and the strengths of the various interactions. These 19 constants must be put in by hand; they are not determined by the theory in any way

Worse, this long list of particles can be broken down into three “families” of quarks and leptons, which are practically indistinguishable from one another. In fact, these three families of particles appear to be exact copies of one another, giving a threefold redundancy in the number of supposedly “elementary” particles (
Figure 5.4
). (It is disturbing to realize that we now have vastly more “elementary” particles than the total number of subatomic particles that were discovered by the 1940s. It makes one wonder how elementary these elementary particles really are.)

The ugliness of the Standard Model can be contrasted to the simplicity of Einstein’s equations, in which everything was deduced from first principles. To understand the aesthetic contrast between the Standard Model and Einstein’s theory of general relativity, we must realize that when physicists speak of “beauty” in their theories, they really mean that their theory possesses at least two essential features: