In Pursuit of the Unknown (28 page)
Read In Pursuit of the Unknown Online
Authors: Ian Stewart

These ratios provide a theoretical basis for a musical scale and led to the scale(s) now used in most Western music. The story is complex, so I'll give a simplified version. For later convenience I'll rewrite a ratio like 3 : 2 as a fraction 3/2 from now on. Start at a base note and ascend in fifths, to get strings of lengths
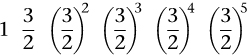
Multiplied out, these fractions become
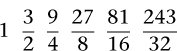
All of these notes, except the first two, are too high-pitched to remain within an octave, but we can lower them by one or more octaves,
repeatedly dividing the fractions by 2 until the result lies between 1 and 2. This yields the fractions
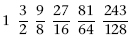
Finally, arrange these in ascending numerical order, obtaining
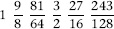
These correspond fairly closely to the notes C D E G A B on a piano. Notice that F is missing. In fact, to the ear, the gap between 81/64 and 3/2 sounds wider than the others. To fill that gap, we insert 4/3, the ratio for the fourth, which is very close to F on the piano. It is also useful to complete the scale with a second C, one octave up, a ratio of 2. Now we obtain a musical scale based entirely on fourths, fifths, and octaves, with pitches in the ratios
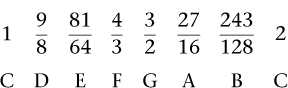
The length is inversely proportional to the pitch, so we would have to invert the fractions to get the corresponding lengths.
We have now accounted for all the white notes on the piano, but there are also black notes. These appear because successive numbers in the scale bear two different ratios to each other: 9/8 (called a tone) and 256/243 (semitone). For example the ratio of 81/64 to 9/8 is 9/8, but that of 4/3 to 81/64 is 256/243. The names âtone' and âsemitone' indicate an approximate comparison of the intervals. Numerically they are 1.125 and 1.05. The first is larger, so a tone corresponds to a bigger change in pitch than a semitone. Two semitones give a ratio 1.05
2
, which is about 1.11; not far from 1.25. So two semitones are close to a tone. Not
very
close, I admit.
Continuing in this vein we can divide each tone into two intervals, each close to a semitone, to get a 12-note scale. This can be done in several different ways, yielding slightly different results. However it is done, there can be subtle but audible problems when changing the key of a piece of music: the intervals change slightly if, say, we move every note up a semitone. This effect could have been avoided if we had chosen a specific ratio for a semitone and arranged for its twelfth power to equal 2. Then two tones would make an exact semitone, 12 semitones would make an octave,
and you could change scale by shifting all notes up or down by a fixed amount.
There is such a number, namely the twelfth root of 2, which is about 1.059, and it leads to the so-called âequitempered scale'. It's a compromise; for example on the equitempered scale the 4/3 ratio for a fourth is 1.059
5
= 1.335, instead of 4/3 = 1.333. A highly trained musician can detect the difference, but it's easy to get used to it and most of us never notice.
The Pythagorean theory of harmony in nature, then, is actually built into the basis of Western music. To explain why simple ratios go hand in hand with musical harmony, we have to look at the physics of a vibrating string. The psychology of human perception also comes into the tale, but not yet.
The key is Newton's second law of motion, relating acceleration to force. You also need to know how the force exerted by a string under tension changes as the string moves, stretching or contracting slightly. For this, we use something that Newton's unwilling sparring partner Hooke discovered in 1660, called Hooke's law: the change in length of a spring is proportional to the force exerted on it. (This is not a misprint for string â a violin string is effectively a kind of spring, so the same law applies.) One obstacle remains. We can apply Newton's laws to a system composed of a finite number of masses: we get one equation per mass, and then do our best to solve the resulting system. But a violin string is a continuum, a line composed of infinitely many points. So the mathematicians of the period thought of the string as a large number of closely spaced point masses, linked together by Hooke's-law springs. They wrote down the equations, slightly simplified to make them soluble; solved them; finally they let the number of masses become arbitrarily large, and worked out what happened to the solution.
John Bernoulli carried out this programme in 1727, and the outcome was extraordinarily pretty, considering what difficulties were being swept under the carpet. To avoid confusion in the descriptions that follow, imagine that the violin is lying on its back with the string horizontal. If you pluck the string it vibrates up and down at right angles to the violin. This is the image to bear in mind. Using the bow causes the string to vibrate sideways, and the presence of the bow is confusing. In the mathematical model, all we have is one string, fixed at its ends, and no violin; the string vibrates up and down in a plane. In this set-up Bernoulli found that the shape of the vibrating string, at any instant of time, was a sine curve. The amplitude of the vibration â the maximum height of this
curve â also followed a sine curve, in time rather than space. In symbols, his solution looked like sin
ct
sin
x
, where
c
is a constant,
Figure 35
. The spatial part sin
x
tells us the shape, but this is scaled by a factor sin
ct
at time
t
. The formula says that the string vibrates up and down, repeating the same motion over and over again. The period of oscillation, the time between successive repeats, is
2Ï/c
.
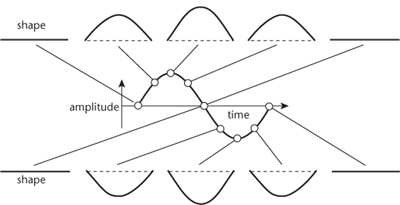
Fig 35
Successive snapshots of a vibrating string. The shape is a sine curve at each instant. The amplitude also varies sinusoidally with time.
This was the simplest solution that Bernoulli obtained, but there were others; all of them sine curves, different âmodes' of vibration, with 1, 2, 3, or more waves along the length of the string,
Figure 36
. Again, the sine curve was a snapshot of the shape at any instant, and its amplitude was multiplied by a time-dependent factor, which also varied sinusoidally. The formulas were sin 2
ct
sin 2
x
, sin 3
ct
sin 3
x
, and so on. The vibrational periods were 2Ï/2
c
, 2Ï/3
c
, and so on; so the more waves there were, the faster the string vibrated.
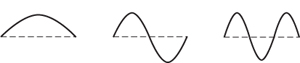
Fig 36
Snapshots of modes 1, 2, 3 of a vibrating string. In each case, the string vibrates up and down, and its amplitude varies sinusoidally with time. The more waves there are, the faster the vibration.
The string is always at rest at its ends, by the construction of the instrument and the assumptions of the mathematical model. In all modes except the first, there are additional points where the string is not
vibrating; these occur where the curve crosses the horizontal axis. These ânodes' are the mathematical reason for the occurrence of simple numerical ratios in the Pythagorean experiments. For example, since vibrational modes 2 and 3 occur in the same string, the gap between successive nodes in the mode-2 curve is 3/2 times the corresponding gap in the mode-3 curve. This explains why ratios like 3 : 2 arise naturally from the dynamics of the vibrating spring, but not why these ratios are harmonious while others are not. Before tackling this question, we introduce the main topic of this chapter: the wave equation.