In Pursuit of the Unknown (54 page)
Read In Pursuit of the Unknown Online
Authors: Ian Stewart

Now the geometry starts to make itself useful. In the cube, there are eight points (strings) and each sphere contains four of them. If I try to fit spheres into the cube, without them overlapping, the best I can manage is two of them, because 8/4 = 2. I can actually find another one, namely the sphere centred on 010. This contains 010, 110, 000, 011, none of which are in the first sphere. So I can introduce a second symbol
b
associated with this sphere. My error-correcting code for messages written with
a
and
b
symbols now replaces every
a
by 101, and every
b
by 010. If I receive, say,
101-010-100-101-000
then I can decode the original message as
a-b-a-a-b
despite the errors in the third and fifth string. I just see which of my two spheres the erroneous string belongs to.
All very well, but this multiplies the length of the message by 3, and we already know an easier way to achieve the same result: repeat the message
three times. But the same idea takes on a new significance if we work in higher-dimensional spaces. With strings of length 4, the hypercube, there are 16 strings, and each sphere contains 5 points. So it
might
be possible to fit three spheres in without them overlapping. If you try that, it's not actually possible â two fit in but the remaining gap is the wrong shape. But the numbers increasingly work in our favour. The space of strings of length 5 contains 32 strings, and each sphere uses just 6 of them â possibly room for 5, and if not, a better chance of fitting in 4. Length 6 gives us 64 points, and spheres that use 7, so up to 9 spheres might fit in.
From this point on a lot of fiddly detail is needed to work out just what is possible, and it helps to develop more sophisticated methods. But what we are looking at is the analogue, in the space of strings, of the most efficient ways to pack spheres together. And this is a long-standing area of mathematics, about which quite a lot is known. Some of that technique can be transferred from Euclidean geometry to Hamming distances, and when that doesn't work we can invent new methods more suited to the geometry of strings. As an example, Hamming invented a new code, more efficient than any known at the time, which encodes 4-bit strings by converting them into 7-bit strings. It can detect and correct any single-bit error. Modified to an 8-bit code, it can detect, but not correct, any 2-bit error.
This code is called the Hamming code. I won't describe it, but let's do the sums to see if it might be possible. There are 16 strings of length 4, and 128 of length 7. Spheres of radius 1 in the 7-dimensional hypercube contain 8 points. And 128/8 = 16. So with enough cunning, it might just be possible to squeeze the required 16 spheres into the 7-dimensional hypercube. They would have to fit exactly, because there's no spare room left over. As it happens, such an arrangement exists, and Hamming found it. Without the multidimensional geometry to help, it would be difficult to guess that it existed, let alone find it. Possible, but hard. Even with the geometry, it's not obvious.
Shannon's concept of information provides limits on how efficient codes can be. Coding theory does the other half of the job: finding codes that are as efficient as possible. The most important tools here come from abstract algebra. This is the study of mathematical structures that share the basic arithmetical features of integers or real numbers, but differ from them in significant ways. In arithmetic, we can add numbers, subtract them, and multiply them, to get numbers of the same kind. For the real numbers we
can also divide by anything other than zero to get a real number. This is not possible for the integers, because, for example,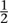 is not an integer. However, it is possible if we pass to the larger system of rational numbers, fractions. In the familiar number systems, various algebraic laws hold, for example the commutative law of addition, which states that 2 + 3 = 3 + 2 and the same goes for any two numbers.
is not an integer. However, it is possible if we pass to the larger system of rational numbers, fractions. In the familiar number systems, various algebraic laws hold, for example the commutative law of addition, which states that 2 + 3 = 3 + 2 and the same goes for any two numbers.
The familiar systems share these algebraic properties with less familiar ones. The simplest example uses just two numbers, 0 and 1. Sums and products are defined just as for integers, with one exception: we insist that 1 + 1 = 0, not 2. Despite this modification, all of the usual laws of algebra survive. This system has only two âelements', two number-like objects. There is exactly one such system whenever the number of elements is a power of any prime number: 2, 3, 4, 5, 7, 8, 9, 11, 13, 16, and so on. Such systems are called Galois fields after the French mathematician Ãvariste Galois, who classified them around 1830. Because they have finitely many elements, they are suited to digital communications, and powers of 2 are especially convenient because of binary notation.
Galois fields lead to coding systems called
ReedâSolomon codes
, after Irving Reed and Gustave Solomon who invented them in 1960. They are used in consumer electronics, especially CDs and DVDs. They are error-correcting codes based on algebraic properties of polynomials, whose coefficients are taken from a Galois field. The signal being encoded â audio or video â is used to construct a polynomial. If the polynomial has degree
n
, that is, the highest power occurring is
x
n
, then the polynomial can be reconstructed from its values at any
n
points. If we specify the values at more than
n
points, we can lose or modify some of the values without losing track of which polynomial it is. If the number of errors is not too large, it is still possible to work out which polynomial it is, and decode to get the original data.
In practice the signal is represented as a series of blocks of binary digits. A popular choice uses 255 bytes (8-bit strings) per block. Of these, 223 bytes encode the signal, while the remaining 32 bytes are âparity symbols', telling us whether various combinations of digits in the uncorrupted data are odd or even. This particular ReedâSolomon code can correct up to 16 errors per block, an error rate just less than 1%.
Whenever you drive along a bumpy road with a CD on the car stereo, you are using abstract algebra, in the form of a ReedâSolomon code, to ensure that the music comes over crisp and clear, instead of being jerky and crackly, perhaps with some parts missing altogether.
Information theory is widely used in cryptography and cryptanalysis â secret codes and methods for breaking them. Shannon himself used it to estimate the amount of coded messages that must be intercepted to stand a chance of breaking the code. Keeping information secret turns out to be more difficult than might be expected, and information theory sheds light on this problem, both from the point of view of the people who want it kept secret and those who want to find out what it is. This issue is important not just to the military, but to everyone who uses the Internet to buy goods or engages in telephone banking.
Information theory now plays a significant role in biology, particularly in the analysis of DNA sequence data. The DNA molecule is a double-helix, formed by two strands that wind round each other. Each strand is a sequence of bases, special molecules that come in four types â adenine, guanine, thymine, and cytosine. So DNA is like a code message written using four possible symbols: A, G, T, and C. The human genome, for example, is 3 billion bases long. Biologists can now find the DNA sequences of innumerable organisms at a rapidly growing rate, leading to a new area of computer science: bioinformatics. This centres on methods for handling biological data efficiently and effectively, and one of its basic tools is information theory.
A more difficult issue is the quality of information, rather than the quantity. The messages âtwo plus two make four' and âtwo plus two make five' contain exactly the same amount of information, but one is true and the other is false. Paeans of praise for the information age ignore the uncomfortable truth that much of the information rattling around the Internet is misinformation. There are websites run by criminals who want to steal your money, or denialists who want to replace solid science by whichever bee happens to be buzzing around inside their own bonnet.
The vital concept here is not information as such, but meaning. Three billion DNA bases of human DNA information are, literally, meaningless unless we can find out how they affect our bodies and behaviour. On the tenth anniversary of the completion of the Human Genome Project, several leading scientific journals surveyed medical progress resulting so far from listing human DNA bases. The overall tone was muted: a few new cures for diseases have been found so far, but not in the quantity originally predicted. Extracting meaning from DNA information is proving harder than most biologists had hoped. The Human Genome Project was a necessary first step, but it has revealed just how difficult such problems are, rather than solving them.
The notion of information has escaped from electronic engineering
and invaded many other areas of science, both as a metaphor and as a technical concept. The formula for information looks very like that for entropy in Boltzmann's approach to thermodynamics; the main differences are logarithms to base 2 instead of natural logarithms, and a change in sign. This similarity can be formalised, and entropy can be interpreted as âmissing information'. So the entropy of a gas increases because we lose track of exactly where its molecules are, and how fast they're moving. The relation between entropy and information has to be set up rather carefully: although the formulas are very similar, the context in which they apply is different. Thermodynamic entropy is a large-scale property of the state of a gas, but information is a property of a signal-producing
source
, not of a signal as such. In 1957 the American physicist Edwin Jaynes, an expert in statistical mechanics, summed up the relationship: thermodynamic entropy can be viewed as an
application
of Shannon information, but entropy itself should not be identified with missing information without specifying the right context. If this distinction is borne in mind, there are valid contexts in which entropy can be viewed as a loss of information. Just as entropy increase places constraints on the efficiency of steam engines, the entropic interpretation of information places constraints on the efficiency of computations. For example, it must take at least 5.8 Ã 10
â23
joules of energy to flip a bit from 0 to 1 or vice versa at the temperature of liquid helium, whatever method you use.
Problems arise when the words âinformation' and âentropy' are used in a more metaphorical sense. Biologists often say that DNA determines âthe information' required to make an organism. There is a sense in which this is almost correct: delete âthe'. However, the metaphorical interpretation of information suggests that once you know the DNA, then you know everything there is to know about the organism. After all, you've got
the
information, right? And for a time many biologists thought that this statement was close to the truth. However, we now know that it is overoptimistic. Even if the information in DNA really did specify the organism uniquely, you would still need to work out how it grows and what the DNA actually does. However, it takes a lot more than a list of DNA codes to create an organism: so-called epigenetic factors must also be taken into account. These include chemical âswitches' that make a segment of DNA code active or inactive, but also entirely different factors that are transmitted from parent to offspring. For human beings, those factors include the culture in which we grow up. So it pays not to be too casual when you use technical terms like âinformation'.
| 16 | The imbalance of nature |
Â
