In Pursuit of the Unknown (61 page)
Read In Pursuit of the Unknown Online
Authors: Ian Stewart

Fig 60
Splitting a triangle into two with right angles.
The perpendicular cuts the side
b
into two pieces. By trigonometry, one piece has length
a
cos
C
, so the other has length
b-a
cos
C
. Let
h
be the height of the perpendicular. By Pythagoras:
a
2
=
h
2
+ (
a
cos
C
)
2
c
2
=
h
2
+ (
b
â
a
cos
C
)
2
That is,
a
2
â
h
2
=
a
2
cos
2
C
c
2
â
h
2
= (
b
â
a
cos C)
2
=
b
2
â 2
ab
cos
C
+
a
2
cos
2
C
Subtract the first equation from the second; now the unwanted
h
2
cancels out. So do the terms
a
2
cos
2
C, and we are left with
c
2
â
a
2
=
b
2
â 2
ab
cos
C
which leads to the stated formula.
1
http://www.17centurymaths.com/contents/napiercontents.html
2
Quoted from a letter John Marr wrote to William Lilly.
3
Prosthapheiresis was based on a trigonometric formula discovered by François Viète, namely
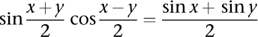
If you owned a table of sines, the formula allowed you to calculate any product using only sums, differences, and division by 2.
1
Keynes never delivered the lecture. The Royal Society planned to commemorate Isaac Newton's tercentenary in 1942, but World War II intervened, so the celebrations were postponed to 1946. The lecturers were the physicists Edward da Costa Andrade and Niels Bohr, and the mathematicians Herbert Turnbull and Jacques Hadamard. The society had also invited Keynes, whose interests included Newton's manuscripts as well as economics. He had written a lecture with the title âNewton, the man', but he died just before the event took place. His brother Geoffrey read the lecture on his behalf.
2
This phrase comes from a letter that Newton wrote to Hooke in 1676. It wasn't new: in 1159 John of Salisbury wrote that âBernard of Chartres used to say that we are like dwarfs on the shoulders of giants, so that we can see more than they.' By the seventeenth century it had become a cliché.
3
Division by zero leads to fallacious proofs. For example, we can âprove' that all numbers are zero. Assume that
a
=
b
. Therefore
a
2
=
ab
, so
a
2
â
b
2
=
ab
â
b
2
. Factorise to get (
a
+
b
)(
a
â
b
) =
b
(
a
â
b
). Divide by (
a
â
b
) to deduce that
a
+
b
=
b
. Therefore
a
= 0. The error is the division by (
a
â
b
), which is 0 because we assumed
a
=
b
.
4
Richard Westfall.
Never at Rest
, Cambridge University Press, Cambridge 1980, p. 425.
5
Erik H. Hauri, Thomas Weinreich, Alberto E. Saal, Malcolm C. Rutherford, and James A. Van Orman. High pre-eruptive water contents preserved in lunar melt
inclusions,
Science Online
(26 May 2011) 1204626. [DOI:10.1126/science. 1204626]. Their results proved controversial.
6
However, it's not coincidence. It works for any differentiable function: one with a continuous derivative. These include all polynomials and all convergent power series, such as the logarithm, the exponential, and the various trigonometric functions.
7
The modern definition is: a function
f
(
h
) tends to a limit
L
as
h
tends to zero if for any
ε
> 0 there exists
δ
> 0 such that |
h
| <
δ
implies that |
f
(
h
)â
L
| <
ε
. Using
any
ε > 0 avoids referring to anything flowing or becoming smaller: it deals with all possible values in one go.
1
The book of Genesis refers to the âfirmament'. Most scholars think this derives from the ancient Hebrew belief that the stars were tiny lights fixed to a solid vault of Heaven, shaped like a hemisphere. This is what the night sky looks like: the way our visual senses respond to distant objects makes the stars appear to be at much the same distance from us. Many cultures, especially in the Middle and Far East, thought of the heavens as a slowly spinning bowl.
2
The Great Comet of 1577 is not Halley's comet, but another of historical importance, now called C/1577 V1. It was visible to the naked eye in 1577
AD.
Brahe observed the comet and deduced that comets were located outside the Earth's atmosphere. The comet is currently about 24 billion kilometres from the Sun.
3
The figure was not known until 1798, when Henry Cavendish obtained a reasonably accurate value in a laboratory experiment. It is about 6.67 Ã 10
â11
newton metre squared per kilogram squared.
4
June Barrow-Green.
Poincaré and the Three Body Problem
, American Mathematical Society, Providence 1997.
1
In 1535 the mathematicians Antonio Fior and Niccolò Fontana (nicknamed Tartaglia, âthe stammerer') engaged in a public contest. They set each other cubic equations to solve, and Tartaglia beat Fior comprehensively. At that time, cubic equations were classified into three distinct types, because negative numbers were not recognised. Fior knew how to solve just one type; initially Tartaglia knew how to solve one different type, but shortly before the contest he figured out how to solve all the other types. He then set Fior only the types that he knew Fior could not solve. Cardano, working on his algebra text, heard about the contest, and realised that Fior and Tartaglia knew how to solve cubics. This discovery would greatly enhance the book, so he asked Tartaglia to reveal his methods.
Eventually Tartaglia divulged the secret, later stating that Cardano had promised never to make it public. But the method appeared in the
Ars Magna
, so Tartaglia accused Cardano of plagiarism. However, Cardano had an excuse, and he also had a good reason to find a way round his promise.
His student Lodovico Ferrari had found how to solve quartic equations, an equally novel and dramatic discovery, and Cardano wanted that in his book, too. However, Ferrari's method required the solution of an associated cubic equation, so Cardano could not publish Ferrari's work without also publishing Tartaglia's.
Then he learned that Fior was a student of Scipio del Ferro, who was rumoured to have solved all three types of cubic, passing just one type on to Fior. Del Ferro's unpublished papers were in the possession of Annibale del Nave. So Cardano and Ferrari went to Bologna in 1543 to consult del Nave, and in the papers they found solutions to all three types of cubic. So Cardano could honestly say that he was publishing del Ferro's method, not Tartaglia's. Tartaglia still felt cheated, and published a long, bitter diatribe against Cardano. Ferrari challenged him to a public debate and won hands down. Tartaglia never really recovered his reputation after that.
1
Summarised in Chapter 12
of: Ian Stewart.
Mathematics of Life
, Profile, London 2011.
1
Yes, I know this is the plural of âdie', but nowadays everyone uses it for the singular as well, and I've given up fighting this tendency. It could be worse: someone just sent me an e-mail carefully using âdice' for the singular and âdie' for the plural.
2
There are many fallacies in Pascal's argument. The main one is that it would apply to any hypothetical supernatural being.
3
The theorem states that under certain (fairly common) conditions, the sum of a large number of random variables will have an approximately normal distribution. More precisely, if (
x
1
, . . .,
x
n
) is a sequence of independent identically distributed random variables, each having mean
μ
and variance Ï
2
, then the central limit theorem states that
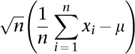
converges to a normal distribution with mean 0 and standard deviation
Ï
as
n
becomes arbitrarily large.
1
Look at three consecutive masses, numbered
n
â 1,
n
,
n
+ 1. Suppose that at time
t
they are displaced distances
u
n
â1
(
t
),
u
n
(
t
), and
u
n
+1
(
t
), from their initial positions on the horizontal axis. By Newton's second law the acceleration of each mass is proportional to the forces that act on it. Make the simplifying assumption that each mass moves through a very small distance in the vertical direction only. To a very good approximation, the force that mass
n
1 exerts on mass
n
is then proportional to the difference
u
n
â1
(
t
) â
u
n
(
t
), and similarly the
force that mass
n
+ 1 exerts on mass
n
is proportional to the difference
u
n
+1
(
t
)â
u
n
(
t
). Adding these together, the total force exerted on mass
n
is proportional to
u
n
â1
(
t
) â 2
u
n
(t) +
u
n+1
(
t
). This is the difference between
u
n
â1
(
t
) â
u
n
(
t
) â
u
n
+1
(
t
), and each of these expressions is also the difference between the positions of consecutive masses. So the force exerted on mass
n
is a
difference between differences
.
Now suppose the masses are very close together. In calculus, a difference â divided by a suitable small constant â is an approximation to a derivative. A difference between differences is an approximation to a derivative of a derivative, that is, a second derivative. In the limit of infinitely many point masses, infinitesimally close together, the force exerted at a given point of the spring is therefore proportional to
â
2
u/âx
2
, where
x
is the space coordinate measured along the length of the string. By Newton's second law this is proportional to the acceleration at right angles to that line, which is the second time derivative
â
2
u/ât
2
. Writing the constant of proportionality as
c
2
we get