Killer Sudoku (25 page)
Authors: Kaye Morgan

That yields more than 150 candidates, if you’re into counting. From here on, the techniques are aimed at reducing that number, bit by bit.
Here’s what the puzzle would look like in dot notation:

The first of these reducing acts is row and box/column and box interactions. The idea here is not to focus on a single space but to see whether segments of rows or columns as broken up by the puzzle subgrids can possibly hold a given number. Then we can eliminate that candidate from other segments of a column or row.
For instance, look at the vertical string of boxes in the left side of the puzzle. The top box contains a 2 right at the top of Column 2, thus eliminating 2s from the segments of Column 1 and Column 3 up there. Moving down to the middle box, Column 3 has two clues in its central segment, and the remaining open space stands right next to a 2 in Row 4. That means that the value 2 can only be found in the segment from Column 1 (we’ve starred the dots representing the possible placements). By process of elimination, 2 can only appear in Column 3 in the bottom left box in the string. Again, we’ve starred the two possible candidates. The net result is two dots Xed out at the bottom of Column 1.

Next, let’s look for naked pairs, where a row, column, or box shares a pair of spaces with two and only two identical candidates.
One just about leaps out at you from the center box—the two remaining open spaces contain dots representing only 3 and 6. Looking up and down Row 5, that eliminates four more candidates.

How about hidden pairs? Like the naked variety, these are twosomes that can only be found in a couple of spaces in a column, row, or box. Unfortunately, they conceal themselves among several other candidates in those spaces. You can see one in the center right box. Check the intersection of Row 5 and Column 7 and see the dots for 7 and 9 alongside the dot for 5. Then look at Row 6: Column 9 has the same 7 and 9 dots in the 2379. You can eliminate three excess candidates.
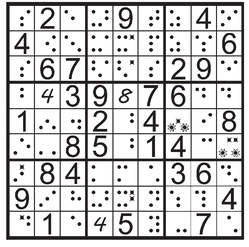
Clumps of candidates can come in larger sizes, maybe even as quintuplets and sextuplets. As a matter of practicality, sudoku solvers rarely search higher than naked or hidden triples. And if you look in the bottom center box, you can find three spaces that represent the only places with shared dots representing 3, 6, and 8. This may be a little difficult—you have to train yourself to ignore eliminated dots while scanning for valid candidates. Bringing the hidden 3, 6, and 8 dots into the open involves Xing out the dots representing five other candidates.

That, fellow solvers, takes us through the first six techniques. Now we start up again. Having eliminated some candidates, it might pay off to scan along the boxes, rows, and columns to see if we may have created any single candidates. And here’s one in Column 6 at the intersection with Row 7—there’s only one dot in the 9 position left, which we’ve starred, putting an X over the dot representing 2. Then, moving up the column to the intersection with Row 2, we find the only remaining 2 in that particular column. We’ve starred that one, too, Xing out the remaining dots.

So here’s the puzzle filled out with all the sure numbers.

At this point we’ve only added six answers to the original thirty clue spaces, but after searching out a couple more hidden pairs, you’ll eliminate enough additional candidates to start a logical chain reaction among the remaining forty-five unknowns.
So here at least is a taste of using positional notation. I purposely kept the sample puzzle simple, because I believe there’s a bit of a learning curve involved. I managed to work all of the less complicated techniques using dots, but I’ll admit that without numbers to fasten on, I had a harder time spotting the hidden triple, much less trying to hunt up X-wings and swordfish. As is the case in most things sudoku, it involves educating the eyes to spot something different.
The dots offer a workable alternative for small-scale puzzles, but they require practice. It’s certainly worth learning if you do a lot of on-the-go sudoku.
If you have fun with it, that’s great. Otherwise, well, there’s the trusty copy machine.
Puzzle Solutions



Other books
The Jake Thomas Trilogy: Book 02 - Sword of Light by Steven A. Tolle
One You Never Leave by Lexy Timms
Hell House by Richard Matheson
Millionaire in a Stetson by Barbara Dunlop
No Survivors by Tom Cain
Ingenue by Jillian Larkin
Journey Into the Flame by T. R. Williams
Demons Undone: The Sons of Gulielmus Series by Holley Trent
Jack's Black Book by Jack Gantos