Mathematics and the Real World (10 page)

The third in the honor roll of the academy of Athens was Aristotle, a pupil of Plato. Aristotle was born in 384 BCE in a city close to Salonika, the capital of Macedonia, and, like Plato, came from an aristocratic family. His father was court physician to the Macedonian king Amyntas. At an early age Aristotle moved to Athens and became a pupil of Plato. Toward the end of Plato's life, or after his death (it is not clear enough which), Aristotle left Athens and founded the Royal Academy in Macedonia. His departure from Plato's academy was apparently the result of a difference of opinion over the scientific direction the academy was taking, and his decision may have been influenced by the fact that he was not appointed to be Plato's successor. He was also concerned about persecution by the Athenians, who considered him a Macedonian, then an enemy of Athens. He founded the Royal Academy of Macedonia, where he also taught Alexander the Great, who became the most prominent figure in the world of that time. Later Aristotle returned to Athens, where he founded his own academy, the Lyceum; its remains can be seen in Athens today. After Alexander's death, the Athenians accused Aristotle of supporting Macedonia, making him flee again. He returned to Macedonia, where he died in 322 BCE.

Aristotle's main contribution to the new mathematics was in the development of logic as a tool for analysis and for drawing conclusions. Syllogisms formulated by Aristotle still serve as the basis of logic. After such a long time, we are so familiar with these rules that their formulation seems simple, correct, and indisputable. We will claim that some of those rules, even if it is easy to agree with them via orderly thought, are not consistent with intuitive thought or with spoken language that developed naturally. We will deal with some of those rules now.

Following the generally accepted practice, we will use letters, say P or Q, to signify a claim or a statement. We will sometimes abbreviate. For example, “P implies Q” means “In every case, if P holds, then Q
must hold” (in mathematics the terminology “In every case, if P is true, then Q must be true” is used). Similarly, we will sometimes write “P” when we mean that P holds (or is true), and we will sometimes write “not P” when we mean that P does not hold (namely, P is false).

The first rule is known as
modus ponens
, which is an example of an intuitive logical claim that may be reasonably assumed to be supported by reason as the result of evolution. The rule is as follows:

If P implies Q

and if P holds

then Q holds.

The following is such a claim: if it is raining, the sidewalk is wet; it is raining now, so the sidewalk is wet. The claim is an intuitive one because in the daily life of every living being, however inferior it may be, there are indications that this relation holds. The Pavlov effect is of the modus ponens type: the ringing of a bell implies that food has arrived. From this to mathematical inferences of the modus ponens type is not far, as we have seen with the animal and human examples cited above.

The next syllogism, the
modus tollens
, is different. It reads as follows:

If P implies Q

and if Q is false

then P is false.

The following is such a claim: if it is raining, the sidewalk is wet; the sidewalk is not wet, so it is not raining now. From a mathematical logic aspect the claim is correct, like the previous one. Yet it is much harder for the brain to absorb. The reason for the difficulty lies in the statement that an event is nonexistent. It is much easier for the brain to accept intuitively that an event occurs and to draw conclusions from it. To draw conclusions from an event that has not occurred is much harder. Many events do not take place, and evolution has not taught the brain to scan those nonexistent events and to draw conclusions from them.

Clearly we must differentiate between two types of negative that appear the same. “The sidewalk is not wet” is translated in the mind as
“the sidewalk is dry,” but it is easier to conclude that it is not raining from the claim that the sidewalk is dry than it is to draw the same conclusion (it is not raining) from the claim that the sidewalk is not wet. We can derive a recommendation from this for anyone speaking or trying to persuade someone of something: steer clear of arguments based on “not.”

The difficulty in applying the syllogisms intuitively has been recognized by logicians, and they developed techniques to identify such errors, or syllogistic fallacies. Here is one example of the many that are available. A person declares the following:

No well-bred person reads tabloids.

I do not read tabloids.

He intends to imply that he is a cultured person. Many would agree, intuitively, at least. But the conclusion is not a logical consequence of his statements.

The connection between these two syllogisms is inherent in the following two rules, also formulated by Aristotle. The first is called the
law of excluded middle
:

Every proposition P either holds or does not hold, that is, P is either true or false.

The second is the
law of contradiction
:

A proposition cannot be both true and false, that is, P and not P cannot coexist.

The proof via reduction ad absurdum discussed above, and which, as we stated, is difficult to understand intuitively, is based on these rules. We want to prove P; we show that by assuming “not P” we arrive at a contradiction, so we can conclude that P holds. It sounds simple, and with a calm and well-ordered analysis the proposition is simple, but the use of this principle intuitively is by no means simple. What evolutionary advantage would a living being obtain from developing this principle intuitively? As will be seen below, the law of excluded middle will play a vital role in the study of the foundations of mathematics in the twentieth century.

Aristotle made other contributions to mathematics, physics, and philosophy, some of which we will describe later in this book. Here we will refer to his involvement in the concept of infinity. The concept of infinity did not appear in any earlier civilizations. When they referred to the term
infinity
, they meant a collection of elements too large to be counted or contained. The concept of infinity did however greatly intrigue the Greeks, especially in connection with the physical structure of the world and how long it had existed. Zeno, following his teacher, Parmenides, alludes to infinity in his paradoxes. We refer to the dichotomy paradox in section 51 and here only recall that the paradox states that a person who wishes to get somewhere would never reach his target, as he has to cover first half of the distance, then one-quarter of the distance, then one-eighth, and so on, in an infinite number of steps. Following this alleged paradox, Aristotle developed an elaborate theory of infinity that we do not describe here as it does not pertain to mathematics. Its contribution to mathematics was to distinguish between
potential infinity
and an infinite collection of elements. Potential infinity in Aristotle's terminology refers to finite collections of unlimited size, such as increasing finite collections of prime numbers. He drew a distinction between these and a set of infinite size. The latter type of infinity was not an acceptable mathematical concept, amenable to logical manipulations. Thus, according to him, the question “Are there more prime numbers or more even numbers?” is not a legitimate question. The study of these concepts was renewed by mathematicians in the nineteenth and twentieth centuries.

The contribution made by Greek mathematics in the classical period was summarized by Euclid. Not much is known about Euclid's life. He lived around 300 BCE and may have studied in the academy of Athens, but he carried out most of his work in Alexandria in Egypt. He was one of the founders of the famous academic center in that city. Although Euclid was active after the classical period, his main mathematical work (which consisted of thirteen volumes), known as Euclid's
Elements
, presented in an orderly and detailed fashion the mathematical knowledge developed in classical Greece. In addition, the
Elements
organized, established, and disseminated
the novel approach developed at that time. Over and above the impressive collection of mathematical findings, the development was based on definitions, axioms, deductive proofs, and defined syllogisms. There are no copies left of the
Elements
that were actually written in Euclid's time. All the versions found (the earliest of which, fragments only, are from the first century CE, i.e., about four hundred years after Euclid; the oldest dated full version is from the ninth century CE) contain remarks, amendments, and additions by those copying the book. From a comparison of the different versions we can nonetheless conclude that Euclid himself organized and arranged the book according to the different subjects, gave the definitions, established his methods of proof, and laid the foundations of the whole approach. It is no wonder that the
Elements
became one of the most widely distributed books in the world of all time and that it has apparently been translated into more languages than any other, except for the Bible.

8. WHAT MOTIVATED THE GREEKS?

Why did the Greeks ask questions whose purposes were not clear and try to answer them via nonintuitive methods?

One reason suggested in the literature is a technical one. The Greeks found mistakes, inconsistencies, and contradictions in the calculations of the Babylonians and the Egyptians, and in order to resolve these they developed a more exact form of mathematics. I am not convinced that this was the reason. If you are uncertain about which of two calculations is more correct or you doubt the accuracy of a calculation, it is reasonable to assume that you would try to perform the calculation more accurately yourself and thus arrive at the right answer. In addition, the Greeks knew that in many areas the calculations of the Babylonians and the Egyptians were more accurate than their own.

A more plausible explanation relates to the political and economic situation in ancient Greece. Although it was a period when many wars were fought between cities and between small kingdoms, in general, a democratic aura prevailed, and political and social philosophies were
highly developed. In an environment in which the study of philosophy is important, when there is no single ruler or government that requires instant achievements from its subjects, when there are no government-appointed committees that determine priorities for research, in an atmosphere when one can question and doubt everything and curiosity-driven study is a highly valued pursuit, in such an atmosphere enormous achievements can be made, even if it takes a very long time to derive benefit from them. To these considerations may be added the fact that the main contributors to developments in research came from established families, and they could study without being concerned with their livelihood and subsistence, a fact that clearly helped them to advance along unorthodox channels. These considerations explain how basic research developed, but they do not explain why it developed in nonintuitive directions and contrary to what evolution would have determined.

A documented explanation for the path followed by the Greeks derives from what are known as illusions. We will expand on this point because it will be relevant in the following chapters. The Greeks were familiar with geometrical or optical illusions, and they therefore tried to prove mathematical propositions without relying on appearances, in other words, relying only on axioms and logical deduction. We will describe two famous illusions from a later period.

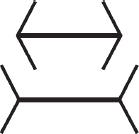
The first is known as the Müller-Lyer illusion, named after the scientist who published it in 1889. The upper line in the diagram seems to be shorter than the lower one, despite the fact that they are of the same length (see the diagram). The usual explanation is that generally, in nature, we see a shape similar to the upper line when looking from the outside, for instance, looking closely at an edge of a three-dimensional cube, whereas we see the lower line as the more distant edge, looking into the cube. The brain uncontrollably corrects the signals that the eye receives, shortens the upper line and lengthens the lower one, in order to obtain the “right” length.

The answer lies in evolution. A correct interpretation of the signals gave an evolutionary advantage and therefore is embedded in the genes. Therefore the way the brain analyzes the information cannot be changed. By directing the eye to see only the horizontal lines we may be able to get the brain to see that the lines shown in a particular way, such as in the diagram, are equal, but we will not be able to do that with lines in situations where the brain interprets spontaneously. In any case, it would be inadvisable to change the way the brain interprets what the eye sees, because if we were to do so we would cause errors in the many situations in which the upper line is actually shorter than the lower one.

The second example is what is known as the Poggendorff illusion, published in 1860. To the untrained observer, the diagonal lines in the following figure do not seem to be sections of one broken straight line, but it can easily be shown that they are. In this instance too there is an explanation why the brain “misleads” us. The brain developed in such a way that it compares angles, not lines. The angles between the diagonals and the vertical lines make the brain create an illusion. Here the illusion does not derive from a correction the brain makes to the data it receives, in other words, a “software” correction; it derives from the “hardware” that the brain employs. The means by which the brain views geometry lead to such errors. In this case too the brain can be trained to avoid the error in specific cases, but it is not possible to carry out a repair that will prevent all such errors.