Mathematics and the Real World (54 page)
Read Mathematics and the Real World Online
Authors: Zvi Artstein

This enables us to base the whole of mathematics on sets and operations on them, including numbers and all the definitions and conclusions drawn from them, and the resulting mathematical theorems. The following is the way to establish the natural numbers from sets. The formal description of the method will be accompanied by an intuitive explanation, but we emphasize that the explanation is not part of the actual process.
We begin with the assumption that an empty set, that is, a set that has no members, exists. We select a mathematical symbol for the empty set, and the symbol normally used is Ø. The explanation is that the set Ø corresponds to the number 0. The set that corresponds to the number 1 is the set that includes the empty set, and only the empty set. We denote this set {Ø}. It is customary to write the elements of the set between the braces. The reason for considering the new set as corresponding to the number 1 is that it contains only one element, and that is the empty set. The next set will be {Ø,{Ø}}, which has two elements, the empty set, and the set that includes the empty set. This set corresponds to the number 2. The set corresponding to the number 3 is {Ø,{Ø}, {Ø,{Ø}}}, and so forth. This formulation is much more complex than simply saying 1, 2, 3, and so forth.
The sole advantage of this type of construction is that it does not use numbers at all, it is formulated entirely in terms of sets. Hence, from here we can take a further step forward and identify other sets that have a finite number of elements equivalent to those we have already constructed by matching the number of elements in those sets to those in our sets, where matching reflects counting. The next step is to define the addition of numbers by means of sets, and that too can be done by combining two sets (the union of two sets) that have no elements in common. That is how small children would act. They calculate three plus four by counting the elements in the union of a set with three members with a set with four members. The same method is used for multiplication and other operations.
We will repeat what we have already mentioned several times. These structures were developed purely and simply to show that mathematics can be based on sets and operations on sets, thus establishing a geometry-free logical basis for mathematics. Nobody thought that this would yield a better intuitive understanding. Some mathematicians opposed this type of development on principle. Leopold Kronecker (1823–1891), for example, is quoted as saying, “God made natural numbers; all else is the work of man.” In other words, there is no need to justify the existence of the natural numbers. Poincaré also saw no need for such structures. Most mathematicians of the period, however, accepted these developments enthusiastically.
The reliance on sets resulted in renewed interest in the concept of infinity. The sets used in defining the natural numbers include a finite number of members, but the sets required to form more complex foundations, such as irrational numbers, contain an infinite number of elements. The question arises naturally, is it possible to implement the arithmetic operations that are translated into logical claims on sets with infinite numbers of elements? As noted previously, evolution did not equip the human brain with the tools to develop intuition about the concept of infinity. Throughout the thousands of years of the development of mathematics in the Babylonian
and Assyrian Empires and in Egypt, the concept of infinity was not considered. The term
infinity
itself was mentioned in the context of very large quantities or large numbers that could not be counted, meaning that it was difficult or impossible to count to such high numbers. Reference to God was also sometimes a reference to the infinite, meaning that God's wisdom and strength were so great that they could not be described. The Greeks were the first to relate to the mathematical infinity, for instance, counting that goes on and on, or lines that did not end. Underlying the interest in the infinite were the questions of whether the world had always existed and if it would exist forever. The Greek's solution to the inability to analyze infinite sets was to make a distinction between potential infinity and an actual infinite collection, a distinction based on Aristotle's methodology. They simply did not think of an infinite collection as a legitimate mathematical entity eligible for consideration. Potential, not actual, infinity—for example, constantly increasing collections of numbers, or finite lines that keep lengthening, or a world that will exist for a constantly increasing length of time—the Greeks considered to be collections of finite sets.
This doctrine of the Greeks persisted, seemingly, but as most mathematical developments were not based on axioms, mathematicians did not hesitate to use the concept of infinity even in the non-potential sense. For example, they referred to infinite lines in researching plane geometry, and thereby even reformulated the axioms, ignoring the distinction between potential and “ordinary” infinity. For many generations there was no re-discussion of the concept of infinity itself, apart from a contribution by Galileo. He noted that although there are “more” natural numbers than squares of natural numbers, there was a one-to-one relation between the natural numbers and their squares, thus:
1, 2, 3, 4,…
1, 4, 9, 16,…
This was also the correspondence that Galileo found between time and the distance that a body falls, as we have seen, and apparently that was the research that brought him to consider infinity. However, this discovery of Galileo's did not go beyond the statement that infinity has strange properties,
a saying that was not accompanied by further study. Now, with the increasing dependence on infinite sets as a basis of mathematics, the time had come to explore that strangeness. That step was taken by Cantor.
Georg Cantor was born in St. Petersburg, Russia, in 1845 to a Christian family of merchants and musicians, a family apparently with Jewish roots. When Georg was eleven, the family moved to Germany, where he excelled in his studies. After studying at the University of Zurich, he returned to Germany and completed his doctorate at the University of Berlin. He studied under Leopold Kronecker and Karl Weierstrass. These two were bitter opponents, and their rivalry also held implications for Cantor himself. On completing his studies he hoped to obtain a post in Berlin or in another major city in Germany, but his path was blocked, apparently by Kronecker. Cantor settled for a post in the less-prestigious University of Halle, Germany, about a hundred miles (160 kilometers) from Berlin, and there he developed the mathematics of infinity. Kronecker was strongly opposed to this new mathematics and, among other things, also blocked Cantor's attempts to publish his papers in professional journals. These rejections, both regarding the posts he had hoped to be appointed to and of his findings, had a lasting effect on the young Cantor and apparently contributed to his mental crises. Cantor spent a large part of his time in the sanatorium in Halle, where he died in 1918. Nevertheless, he saw his theory accepted by the mathematics community, even with the logical difficulties and paradoxes it brought to the foundations of mathematics.
We will now give a short description of Cantor's theory. Its starting point is the same analysis of Galileo's that we spoke of above. Cantor suggested that we agree to state that both sets have “the same number” of elements if the elements of one can be matched one-to-one (bijection) with the elements of the second. Thus the set of natural numbers and the set of their squares have the same number of elements. Similarly, he showed that the set of rational numbers and the set of natural numbers have the same number of elements, although the rational numbers are spread tightly all along the real number line, while the natural numbers have empty spaces between them.
The next question was, do all infinite sets have the same number of elements? Here Cantor made a surprising discovery. He proved that the set of real numbers and the set of rational numbers do not have the same number of elements. Every rational number can be represented by a point on the straight line, but there is no such match for all the real numbers. From that he derived that the latter set had “more members.” He denoted the “number” of members in the set of natural numbers as
aleph-null
, denoted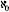 , and sets with a number of elements like the set of natural numbers he called countable infinite sets. Cantor called the indication of the size of the set its power, or cardinality. Other powers of sets greater than that of the natural numbers he denoted
, and sets with a number of elements like the set of natural numbers he called countable infinite sets. Cantor called the indication of the size of the set its power, or cardinality. Other powers of sets greater than that of the natural numbers he denoted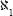 ,
,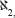 and so on. It is not clear why Cantor chose to use the Hebrew letter aleph for this mathematical notation, and some relate that choice to his family's possible Jewish roots. Others note that as the Bible, including Hebrew writing, was studied by religious Christian groups in Germany, Cantor was familiar with Hebrew, and that was why he chose the first letter in the Hebrew alphabet, aleph. He denoted the power of the set of the real numbers C, the first letter of the Latin word
and so on. It is not clear why Cantor chose to use the Hebrew letter aleph for this mathematical notation, and some relate that choice to his family's possible Jewish roots. Others note that as the Bible, including Hebrew writing, was studied by religious Christian groups in Germany, Cantor was familiar with Hebrew, and that was why he chose the first letter in the Hebrew alphabet, aleph. He denoted the power of the set of the real numbers C, the first letter of the Latin word
continuum
. Cantor went on to prove that the power of C was the same as that of the set of subsets of the natural numbers. Therefore, just as the number 2
n
measures the number of subsets of the set with
n
elements (we recommend the reader to check this), Cantor denoted the power of C by 2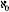 .
.
Cantor also developed the arithmetic of powers. For example, it can be seen that the equality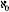 +
+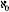 =
=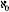 holds when the sum is defined in the same way as we defined the sum of numbers by means of sets. That is, the sum of powers is the power of the union of disjoint sets that have the corresponding powers. And indeed, both even numbers and odd numbers are of power
holds when the sum is defined in the same way as we defined the sum of numbers by means of sets. That is, the sum of powers is the power of the union of disjoint sets that have the corresponding powers. And indeed, both even numbers and odd numbers are of power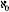 , and that is also the power of their union, that is, all the natural numbers. Cantor proved generally that the collection of subsets of a non-empty set is of a greater power than that of the set itself, thus ensuring that, as with the numbers themselves, the possible powers of sets can increase boundlessly.
, and that is also the power of their union, that is, all the natural numbers. Cantor proved generally that the collection of subsets of a non-empty set is of a greater power than that of the set itself, thus ensuring that, as with the numbers themselves, the possible powers of sets can increase boundlessly.