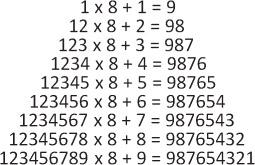Mathematics and the Real World (62 page)
Read Mathematics and the Real World Online
Authors: Zvi Artstein

Johann Bernoulli's solution to the brachistochrone problem remained a one-off trick, attractive in form, but with almost no further use. In contrast, the clumsy and complicated method developed by Jacob Bernoulli grew into an extensive and important area of mathematics called the calculus of variations. This field of mathematics is implemented widely and has many applications, both within and outside mathematics, and it presents mathematical challenges that so far are in the area of mathematics for its own sake.
In the above examples, and in others we have not described, the connection can be seen between the abstract study of mathematics and its uses. Sometimes the practical use of mathematics leads to an abstract mathematical theory that develops into mathematics for its own sake, which often results in new real practical uses. On other occasions, research starts with questions that mathematicians ask themselves, prompted by purely mathematical curiosity, that apparently are of no interest for any practical purpose, yet whose solutions are found to have significant use outside the world of mathematics. Is this merely a coincidence? Or perhaps a statistical illusion? Or perhaps it is the inevitability of reality?
We may well be the victims of an illusion. For hundreds of years, mathematicians developed many and varied theories, most of which were assigned to oblivion because of their irrelevance. Theories that found their place within sciences other than mathematics have wider exposure and are more generally known than those that remain within the area of “pure” mathematics,
so that the use of this “applied” mathematics seems to us more frequent than it really is. Similarly, when researchers in natural sciences look for a new mathematical theory to explain their findings, they search among theories already developed, including those developed as mathematics for its own sake, and that can lead to the illusion that mathematics for its own sake plays a central role in applications. There may be another explanation, however, that seems to me to be more reasonable: mathematics for its own sake was also developed by the human brain, a brain that learned to reveal patterns that appear in nature. That brain is not capable of revealing patterns that are totally detached from nature. When the mathematical pattern can be used by nature, it is not surprising that nature actually does use it.
65. THE BEAUTY, EFFICIENCY, AND UNIVERSALITY OF MATHEMATICS
It is generally accepted that beauty is a matter of taste, yet certain fundamentals of beauty and enjoyment are common to most human beings. Like other aspects of human conduct, the sources of enjoyment and the relation to beauty were formed by evolution. A prime example of the emotion inspired by beauty is that felt on recognizing patterns, symmetries, and so on. Recognizing a pattern or symmetry affords great pleasure, and, in surprising situations or places where one does not expect to find order, discovering them can give even greater delight. That is true in all areas of life, from natural scenery, to the plastic arts, to social and cultural environments, and so on. Patterns are also the basis of mathematical practice. Hence, every new theorem or new geometrical law that we encounter has the potential to give us pleasure. In most such cases, the patterns, and, hence, the enjoyment, are of the intellectual rather than visual sort. In many instances, before enjoying the mathematical pattern, we have to contend with terminology that is sometimes hard even for professionals to understand, learn special jargon, and also imbibe the mathematical content. These are some of the factors that keep much of the general public away from mathematics and its pleasures. I remember a cartoon showing three mathematicians in
a jolly mood next to a blackboard covered with complex formulae, and one is saying to the others, “I knew you'd burst out laughing.” There are indeed professional jokes and professional pleasures in mathematics just as in other disciplines. I will nevertheless repeat a statement presented at the beginning of this book: just as one can derive pleasure from music without being able to read a score, so can one derive pleasure from mathematical patterns without being able to read the mathematical notes, and one certainly can get enjoyment from knowing how mathematics fulfills its role as a tool for explaining nature. I hope that “non-mathematical” readers who have reached this section will agree with that statement.
Nonetheless, the general public is sometimes presented with other examples of the enjoyment and beauty in mathematics. Not long ago I received an e-mail with the following tower-shaped table, alongside other similar tables, under the title “The Beauty of Mathematics.”
The table was presented in lovely colors, every digit in another color, and the colors accentuated the special pattern. Some of my acquaintances, of course including the person who had sent it to me, expressed their wonder at the beauty of this mathematics. I did not find anything interesting or special, in a mathematical sense, in this tower. It was pleasing to the eye, and its colors were attractive. The order that the arithmetic exercises reflected was also interesting and enjoyable, but it did not contain any marked element of surprise for me. I did not find any beauty in it from a mathematical aspect. I agree that the arithmetic reflected by the tower
is aesthetic, but that is not the beauty of mathematics. If I were to delve deeper, or if someone were to show me that hidden within the structure is a special pattern, then I might find beauty in the equalities that constitute the tower. But I did not find it in the tower as it is.
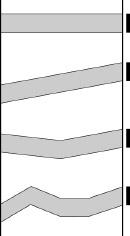
Here is another example. One of Israel's daily newspapers published a diagram and puzzle under the heading “You Can Enjoy Geometry” (see my sketch of the puzzle below). The sketch shows four strips that could be considered bridges from one bank of an imaginary river to the other. The width of each band is the same and is constant along its whole length, but some are straight and some change direction, as in the diagram. The puzzle is: Which bridge would be the cheapest to paint, and which the most expensive?
The answer is that there is no difference in the costs. All the bridges have the same area. The solution can be seen “clearly” (the word used by the paper; one could argue with the use of that term) if the picture is turned onto its side. Every bridge consists of parallelograms with the same sized bases, and the widths of the bridges stays the same from one bank of the river to the other, and the sum of the heights of the parallelograms is the same for all the bridges. Hence (as anyone who learned
and remembers
basic geometry will know), the areas of the bridges are all equal. And I ask, “What is enjoyable in this?” I did not get any pleasure from it, firstly because I did not find the solution myself. Moreover, whoever set the puzzle thought that I ought to see the answer immediately, and that is
another reason why I did not enjoy it. I was also left with the feeling that I had been misled. The question was which bridge would be the cheapest to paint, and which the most expensive. To my mind, if the question is worded like that, it implies that one of the bridges has the largest area and one has the smallest, and if that is not the case, then I have been misled. Even if I derived a little enjoyment from the trick that I learned, to place the picture on its side, it was mixed with some disappointment that it was after all just a trick, let alone the fact that you do not need to place a parallelogram on its side to calculate its area; but that is how it is taught in schools. I have no objections to those who do enjoy such puzzles. To anyone like me who does not enjoy them I would say, don't think that you cannot get pleasure from mathematics. It is possible to get enjoyment from tricks, or to be frustrated that you didn't manage to find the trick yourself, but tricks of this type are not an essential part of mathematics.
A similar message is derived from this well-known story about John von Neumann. A friend asked him the following question: Two trains start moving toward each other at the same time from positions a hundred kilometers apart at a speed of fifty kilometers an hour. At the same time a bee starts flying at three hundred kilometers an hour from one train toward the other until it reaches it, and then starts flying back to the first train, until it reaches it, and then turns around again. This continues until the trains meet. What total distance does the bee fly? Before we give von Neumann's answer, we observe that there are two ways of solving the problem. The simple way is to note that the trains meet after exactly one hour, and in that time the bee will have flown three hundred kilometers. The second, more complicated, method is to calculate the distance that the bee will have flown until it first meets the second train (this requires solving a not-particularly difficult equation), then to calculate the distance it flies until it is back at the first train, and continue in this manner. This gives an infinite series that can be added relatively simply (for anyone who remembers the formula), and the result, if no mistakes are made, is three hundred kilometers. Now back to von Neumann. He thought briefly (he was known to be a very quick thinker) and then gave the right answer, three hundred kilometers. The friend confirmed that von Neumann's answer was indeed
correct and then complimented him, saying, “One can see that you are an excellent mathematician. Some fools,” he continued, “calculate the sum of the infinite series in order to get to the answer.” Von Neumann looked at him in surprise and asked, “Is there another way?”
The message I am trying to convey is that mathematics is not a collection of tricks. On the contrary; the essence of mathematics is ordered and well-organized analysis of patterns already revealed or that still need to be found. We saw an example of the difference between a trick and a theory in the instance of the brachistochrone in the previous section. It is acceptable and possible to benefit from tricks, but the real beauty of mathematics derives from the patterns and rules found in mathematics, and the pleasure from, and sometimes amazement at, the link to nature and to applications that the patterns and rules open up for us. I believe that nearly all the material discussed in the book up until now reflects the beauty of that sort in mathematics.
Another aspect related to the beauty and pleasure of mathematics is the sometimes-wonderful efficiency of mathematics as an instrument for describing and explaining natural phenomena. The question why is it just mathematics that is so appropriate to the description of nature arose already in ancient times, and it reappeared even more pointedly following the revolution led by Maxwell, which led to the theory of relativity and quantum theory.
Until that revolution, which symbolizes the start of the modern era in science, the question was not why does mathematics describe nature so well, but why do natural phenomena occur according to any system of rules? Why does nature itself have to follow laws that we call laws of nature? Why are there such clear patterns in nature? Why is the law of gravity on Earth the same as the law of gravity on the Moon, and apparently the same as the law of gravity in other galaxies? Why is a small, finite number of particles the component that constitutes all known materials in nature? And why can we find ordered patterns, to the extent even of a structure of mathematical groups, that determine how those particles arrange themselves? We could extend this list of questions. There are no
standard scientific answers to these questions, and interest and involvement in them is usually placed in what philosophers call the transcendental sphere. For example, the saying that nature is based on mathematics is attributed to Galileo Galilei, and even the Christian Church at the time of the Renaissance agreed that God in his great wisdom used mathematics to create such a wonderful world. That of course is not a satisfactory answer to the question of why mathematics is the appropriate instrument to be used in describing and analyzing nature. We should bear in mind that the very understanding that nature expresses clear sets of laws is not natural or self-explanatory. The ancient civilizations discovered that such laws existed but did not delve into them or try to fathom them. Also, the Greeks, who declared that the laws of nature could be described successfully through logic, needed hundreds of years to really absorb that understanding into their scientific view of the world. The fact that the earthly laws of motion were the same as the heavenly laws of motion was discovered, and then accepted, only a little more than three hundred years ago.