Nonplussed! (9 page)
Authors: Julian Havil

Also, calculators (and computers) eventually cannot cope with very large numbers and this result provides the mechanism for doing just that, as we shall now see.
A Practical Application
The Birthday Paradox is more than a novelty; in fact, it has applications in many areas, including cryptography, sorting and the somewhat esoteric code numbers called GUIDs, which identify the product of a particular package of a particular computer. Using the estimate derived from Halmos’s ideas, we can look at these Globally Unique Identifiers (GUIDs).
Each GUID is 128 bits long, which means that it can be written as a 32 digit hexadecimal (base 16) number. There are many
Internet sites which will provide such a number using one algorithm or another and, in particular, one site contained the following:
GUID.org is an Internet service that assigns anonymous user IDs to web browsers. These anonymous IDs can then be used by other web sites for many purposes. For example, a site may use your GUID to recognize you when you return.
GUID.org works by assigning each browser a unique, essentially random 16-byte user ID, which is represented as 32 hexadecimal digits. This ID is constructed by applying a MD5 hash to a string concatenated from the IP address of the requestor, the IP address of this server, the date, and the time of day in ticks. The ID is then set as a cookie from GUID.org.
Never mind about the computer jargon, the important matter is that a GUID is randomly generated, 128 bits long and supposedly unique, and it may be important that it is unique if it is to be used to identify a revisit to a site. It happens that, when the author requested a GUID from the site, the GUID assigned was

using the standard digits {1,2,3,
…,
9,A,B,
…,
F} of the hexadecimal number system.
Could the number be safely used as a unique identity code? There is a chance that this random process will result in a GUID which has been used before; but what chance? This is just a disguised form of the birthday problem with
n =
2
128
. Using the above result we can see that the total number of GUIDs generated before the odds are in favour of a clash is about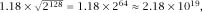 which is vastly big.
which is vastly big.
To give an idea of the size of things, if 100000 GUIDs were being generated every hour of every day it would take about 22 billion years to generate this number – and the universe is only about 12–15 billion years old. The system seems reasonably safe!
As a final hint as to the generality of the application of the result, the reader might wish to pursue the following item:
M. H. Gail, G. H. Weiss, N. Mantel and S. J. O’Brien (1979), A solution to the generalized birthday problem with application to allozyme screening for cell culture contamination,
Journal of Applied Probability
16:242–51.

THE SPIN OF A TABLE
In mathematics, you don’t understand things. You just get used to them.
John von Neumann
The Original Problem
Martin Gardner brought to the wider world ‘a delightful combinatorial problem of unknown origin’ in his February 1979 column in
Scientific American
. He commented that Robert Tappay of Toronto had passed it to him, who believed it to have originated in Russia:
A square table stands on a central column, which allows it to rotate freely in a horizontal plane. At each corner there is a pocket too deep to allow the contents to be seen and of a size to accommodate an ordinary, empty wine glass. An electronic mechanism is fitted so that, with each pocket containing a single wine glass, a bell will ring if all glasses are oriented in the same direction. The experiment begins with the glasses distributed between the pockets, their orientation randomly chosen. A person sits at the table and chooses two pockets simultaneously, from which the glasses are removed, examined and replaced as that person decides.
The table is then spun in such a way that the person is unable to tell which side now is in front. The process is then repeated indefinitely.
After any repetition the bell might or might not ring simply by chance but the problem is to find a procedure which will ensure that it does ring after a finite number of spins. This is not a case of probability, not a matter of arguing that eventually the bell
must surely
ring: it will ring with absolute certainty.
Two Simpler Cases
As is so often the case, it helps to illuminate matters if we consider simpler cases, in this case a table with just two pockets, modelled by a rod with pockets at either end, or three pockets, modelled by an equilateral triangle with pockets at each vertex.
figure 4.1
provides diagrams of such tables.
The first thing to realize is that we can assume that the initial random placement has the glasses in different orientations – otherwise the bell would ring straight away.
With two pockets the problem is entirely trivial: since the bell does not ring when the glasses are put in the pockets, when the table has stopped spinning look at both glasses and invert one of them to ensure that they both have the same orientation.
Now suppose that the table is in the shape of an equilateral triangle, with a pocket at each vertex. The following procedure will guarantee that the bell rings:
(1) Reach into any pair of pockets; if the glasses are oriented in the same direction invert them both and the bell will ring. Otherwise the glasses will be facing in different directions, so invert the glass that is facing down.
(2) If the bell does not ring, spin the table and reach into any two pockets; if both glasses are turned up, invert both and the bell will ring. If they are turned in opposite directions, invert the glass turned down and the bell will ring.
From these two simple cases we can see that the result for four pockets is at least plausible and we are now ready to consider this original puzzle.
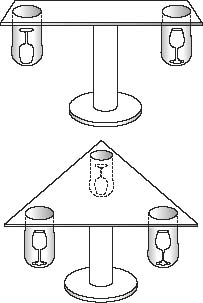
Figure 4.1.
Two simpler situations
The Original Problem Solved
Figure 4.2
shows our new table. An initial, important observation for this case is that the selection of the pockets has essentially two forms: a side pair or a diagonal pair. It is also clear that these choices must alternate, otherwise we could go on repeating ourselves forever. With that in mind we can look at a procedure which guarantees that the bell will ring.
(1) Reach into a diagonal pair of pockets and orient the glasses to be the same way up.
(2) Given that the bell does not ring, spin the table and reach into two adjacent pockets. If the glasses are both turned up, leave them, otherwise invert the glass that is turned down. If the bell does not ring, it is certain that there are three glasses with the same orientation.
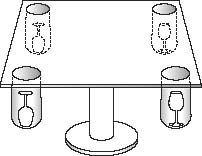
Figure 4.2.
The square table
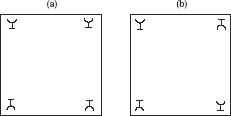
Figure 4.3.
The two assured orientations
(3) Spin the table and then reach into a diagonal pair of pockets. If one of the glasses is turned down, invert it and the bell will ring. If both are turned up, invert one of them, in which case the orientations will be as in
figure 4.3
(a).
(4) Spin the table, reach into two adjacent pockets and invert the glasses. If they were both of the same orientation, the bell will ring, otherwise the glasses will now be as in
figure 4.3(b)
.
(5) Spin the table, reach into a diagonal pair of pockets and invert both glasses. The bell will definitely ring.
With this argument, the problem is solved in at most five spins of the table (which is minimal). If we decide to sacrifice minimalism (and thought), the following seven steps solve the problem automatically:
(1) Invert any diagonal pair.
(2) Invert any adjacent pair.
(3) Invert any diagonal pair.
(4) Invert any single glass.
(5) Invert any diagonal pair.
(6) Invert any adjacent pair.
(7) Invert any diagonal pair.
The Problem Generalized
In the end, a table with two pockets presents a trivial problem, one with three pockets an easy problem and one with four pockets a rather more subtle problem. What about a table with five pockets? The answer is that the situation changes radically since, with a five-sided (or greater) table, there is no algorithm which will guarantee that the bell will ring in a finite number of moves. (In
chapter 6
we will meet a second situation in which matters change radically at the fifth level, a phenomenon which is far from uncommon in mathematics.)
The March 1979
Scientific American
column provided the solution to the original problem. Evidently, mathematicians had been active between the February and March issues, since the March column also mentions two generalizations suggested by Ronald L. Graham and Persi Diaconis:
(1) Can the bell be made to ring if the player is replaced by an ‘octopus’ with
k
hands sitting at a table with
n
sides?
(2) Can the bell be made to ring if the glasses are replaced by objects which can occupy more than two positions?
They provided a partial solution to the first question, showing that with a table having a prime number of sides
n
the minimum number of hands needed to guarantee the bell ringing is
n-
1 and that the minimum number is bounded above by
n-
2 otherwise.
Of course, their result decides the case for the five-sided table mentioned above; there,
k =
2 and
n =
5.
Subsequently, William T. Laaser and Lyle Ramshaw, both of Stanford, solved the first generalization completely. Their result is that the minimum number of hands,
k
, required to ensure that the bell will ring for an
n
-sided table is
k = (
1 −1
/p)n
, where
p
is the largest prime factor of
n
(a formula conjectured by James Boyce). Of course, this reduces to the above result in the case where
n
is prime (and therefore
n = p
).
The full exposition of the Laaser–Ramshaw result (Probing the rotating table,
Mathematical Gardner
, 1981, 288–307) is too long for inclusion here but we will consider the first part of it, which establishes that (1 − 1
/p)n
is a lower bound on
k
; that is, if
k < (
1 − 1
/p)n
, it is impossible to guarantee that the bell will ring.
First we will establish a preliminary result.
Consider the set of integers
{
0,1,2,
…,p-
1} reduced modulo the prime
p
. If we start at any position
r
and move through the integers in steps of 1 (reducing modulo
p
), it is evident that we will visit each integer before we reach our starting point again. Now suppose that we move in steps of size
j
(where 2 ≤
j
≤
p -
1). We will generate the set of integers
{r + αj
: 0 ≤
α
≤
p -
1}, modulo
p
, as we move through the integers and if two of these numbers are equal it must be that
r + αj = r + ßj
, modulo
p
, and this means that
(ß - α)j
is divisible by
p
. Since
p
is prime and cannot possibly divide
j
, it must be that
p
divides
ß - α
and this makes
ß = α + Np
. In short, any walk around the integers will visit each one of them once before returning to the starting point.
With that in place consider the Laaser–Ramshaw result in two parts:
(1) Suppose that
n = p
is prime. If the player has fewer than
p -
1 hands, then he has no winning strategy.
If the player has fewer than
p -
1 hands, any probe of the table will leave at least two pockets untested; call these pockets
gaps
and suppose that two of them are a distance
j
apart. Our
preliminary argument shows that, if we start at any pocket and walk around the table in steps of length
j
, we will visit every pocket before returning to the starting point. Since the pockets must contain glasses of both orientations, it must be that our journey will at some stage cause us to step from a glass of one orientation to one of another, precisely a distance
j
apart. If the table happens to align itself so that the gaps
j
apart in the probe pattern match the glasses of different orientation, the bell cannot ring. The procedure can be repeated indefinitely, which shows that no ringing of the bell can be guaranteed.