Statistics Essentials For Dummies (27 page)

increases, the standard error (entire fraction) increases. A larger standard error means a larger margin of error and a wider confidence interval.
More variability in the original population increases the margin of error, making the confidence interval wider. However, don't let that discourage you. This increase can be offset by increasing the sample size. (Remember the sample size,
n
, appears
in the denominator of the standard error formula,
, so an
increase in
n
results in a decrease in the margin of error.)
Confidence Interval for a Population Mean
When the characteristic that's being measured (such as income, IQ, price, height, quantity, or weight) is
numerical,
people often want to estimate the
mean
(average) value for the population. You estimate the population mean by using a sample mean plus or minus a margin of error. The result is a
confidence interval for a population mean,.
The formula for a CI for a population mean is
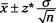
where
is the sample mean;
is the population standard deviation;
n
is the sample size; and
z*
is the appropriate value from the
Z
-distribution for your desired confidence level (see Table 7-1 for values of
z*
for given confidence levels).
For example, suppose you work for the Department of Natural Resources and you want to estimate, with 95% confidence, the mean (average) length of the walleyes in a fish hatchery pond. (Assume the population standard deviation (
) is 2.3 inches.) Because you want a 95% confidence interval, your
z
*
-value is 1.96. Suppose you take a random sample of
n
= 100 walleyes and find the average length () is 7.5 inches. To find the margin of error, multiply 1.96 times 2.3 divided by the square root of 100 to get plus or minus 1.96 * (2.3/10) = 0.45 inches.
Your 95% confidence interval for the mean length of the walleyes in this fish hatchery pond is 7.5 inches plus or minus 0.45 inches. (The lower end of the interval is 7.5 - 0.45 = 7.05 inches; the upper end is 7.5 + 0.45 = 7.95 inches.) You can say that a range of likely values for the average length of the walleyes in this entire pond is between 7.05 and 7.95 inches, based on your sample, with a confidence level of 95%.
When your sample size is small (under 30), you use the appropriate value on the
- distribution with
- 1 degrees of freedom instead of
z*
(see Table A-2 in the appendix).