The Code Book (54 page)

Although traffic analysis, tempest attacks, viruses and Trojan horses are all useful techniques for gathering information, cryptanalysts realize that their real goal is to find a way of cracking the RSA cipher, the cornerstone of modern encryption. The RSA cipher is used to protect the most important military, diplomatic, commercial and criminal communications—exactly the messages that intelligence gathering organizations want to decipher. If they are to challenge strong RSA encryption, cryptanalysts will need to make a major theoretical or technological breakthrough.
A theoretical breakthrough would be a fundamentally new way of finding Alice’s private key. Alice’s private key consists of
p
and
q
, and these are found by factoring the public key,
N
. The standard approach is to check each prime number one at a time to see if it divides into
N
, but we know that this takes an unreasonable amount of time. Cryptanalysts have tried to find a shortcut to factoring, a method that drastically reduces the number of steps required to find
p
and
q
, but so far all attempts to develop a fastfactoring recipe have ended in failure. Mathematicians have been studying factoring for centuries, and modern factoring techniques are not significantly better than ancient techniques. Indeed, it could be that the laws of mathematics forbid the existence of a significant shortcut for factoring.
Without much hope of a theoretical breakthrough, cryptanalysts have been forced to look for a technological innovation. If there is no obvious way to reduce the number of steps required for factoring, then cryptanalysts need a technology that will perform these steps more quickly. Silicon chips will continue to get faster as the years pass, doubling in speed roughly every eighteen months, but this is not enough to make a real impact on the speed of factoring-cryptanalysts require a technology that is billions of times faster than current computers. Consequently, cryptanalysts are looking toward a radically new form of computer, the
quantum computer
. If scientists could build a quantum computer, it would be able to perform calculations with such enormous speed that it would make a modern supercomputer look like a broken abacus.
The remainder of this section discusses the concept of a quantum computer, and therefore it introduces some of the principles of quantum physics, sometimes called quantum mechanics. Before going any further, please heed a warning originally given by Niels Bohr, one of the fathers of quantum mechanics: “Anyone who can contemplate quantum mechanics without getting dizzy hasn’t understood it.” In other words, prepare to meet some rather bizarre ideas.
In order to explain the principles of quantum computing, it helps to return to the end of the eighteenth century and the work of Thomas Young, the English polymath who made the first breakthrough in deciphering Egyptian hieroglyphics. A fellow of Emmanuel College, Cambridge, Young would often spend his afternoons relaxing near the college duck pond. On one particular day, so the story goes, he noticed two ducks happily swimming alongside each other. He observed that the two ducks left two trails of ripples behind them, which interacted and formed a peculiar pattern of rough and calm patches. The two sets of ripples fanned out behind the two ducks, and when a peak from one duck met a trough from the other duck, the result was a tiny patch of calm water-the peak and the trough canceled each other out. Alternatively, if two peaks arrived at the same spot simultaneously, then the result was an even higher peak, and if two troughs arrived at the same spot simultaneously, the result was an even deeper trough. He was particularly fascinated, because the ducks reminded him of an experiment concerning the nature of light which he conducted in 1799.
In Young’s earlier experiment he had shone light at a partition in which there were two narrow vertical slits, as shown in
Figure 71(a)
. On a screen some distance beyond the slits, Young expected to see two bright stripes, projections of the slits. Instead he observed that the light fanned out from the two slits and formed a pattern of several light and dark stripes on the screen. The striped pattern of light on the screen had puzzled him, but now he believed he could explain it wholly in terms of what he had seen on the duck pond.
Young began by assuming that light was a form of wave. If the light emanating from the two slits behaved like waves, then it was just like the ripples behind the two ducks. Furthermore, the light and dark stripes on the screen were caused by the same interactions that caused the water waves to form high peaks, deep troughs and patches of calm. Young could imagine points on the screen where a trough met a peak, resulting in cancelation and a dark stripe, and points on the screen where two peaks (or two troughs) met, resulting in reinforcement and a bright stripe, as shown in
Figure 71(b)
. The ducks had provided Young with a deeper insight into the true nature of light, and he eventually published “The Undulatory Theory of Light,” an all-time classic among physics papers.
Nowadays, we know that light does indeed behave like a wave, but we know that it can also behave like a particle. Whether we perceive light as a wave or as a particle depends on the circumstances, and this ambiguity of light is known as wave-particle duality. We do not need to discuss this duality any further, except to say that modern physics thinks of a beam of light as consisting of countless individual particles, known as photons, which exhibit wave-like properties. Looked at this way, we can interpret Young’s experiment in terms of photons flooding the slits, and then interacting on the other side of the partition.
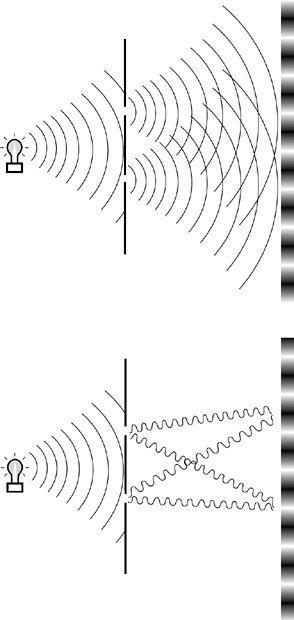
Figure 71
Young’s slits experiment viewed from above. Diagram (a) shows light fanning out from the two slits in the partition, interacting and creating a striped pattern on the screen. Diagram (b) shows how individual waves interact. If a trough meets a peak at the screen, the result is a dark stripe. If two troughs (or two peaks) meet at the screen, the result is a bright stripe.
So far, there is nothing particularly strange about Young’s experiment. However, modern technology allows physicists to repeat Young’s experiment using a filament that is so dim that it emits single photons of light. Photons are produced individually at a rate of, say, one per minute, and each photon travels alone toward the partition. Sometimes a photon will pass through one of the two slits, and strike the screen. Although our eyes are not sensitive enough to see the individual photons, they can be observed with the help of a special detector, and over a period of hours we could build up an overall picture of where the photons are striking the screen. With only one photon at a time passing through the slits, we would not expect to see the striped pattern observed by Young, because that phenomenon seems to depend on two photons simultaneously traveling through different slits and interacting with each other on the other side. Instead we might expect to see just two light stripes, simply projections of the slits in the partition. However, for some extraordinary reason, even with single photons the result on the screen is still a pattern of light and dark stripes, just as if photons had been interacting.
This weird result defies common sense. There is no way to explain the phenomenon in terms of the classical laws of physics, by which we mean the traditional laws that were developed to explain how everyday objects behave. Classical physics can explain the orbits of planets or the trajectory of a cannonball, but cannot fully describe the world of the truly tiny, such as the trajectory of a photon. In order to explain such photon phenomena, physicists resort to quantum theory, an explanation of how objects behave at the microscopic level. However, even quantum theorists cannot agree on how to interpret this experiment. They tend to split into two opposing camps, each with their own interpretation.
The first camp posits an idea known as
superposition
. The superpositionists begin by stating that we know only two things for certain about the photon-it leaves the filament and it strikes the screen. Everything else is a complete mystery, including whether the photon passed through the left slit or the right slit. Because the exact path of the photon is unknown, superpositionists take the peculiar view that the photon somehow passes through both slits simultaneously, which would then allow it to interfere with itself and create the striped pattern observed on the screen. But how can one photon pass through both slits?
Superpositionists argue along the following lines. If we do not know what a particle is doing, then it is allowed to do everything possible simultaneously. In the case of the photon, we do not know whether it passed through the left slit or the right slit, so we assume that it passed through both slits simultaneously. Each possibility is called a
state
, and because the photon fulfills both possibilities it is said to be in a
superposition of states
. We know that one photon left the filament and we know that one photon hit the screen on the other side of the partition, but in between it somehow split into two “ghost photons” that passed through both slits. Superposition might sound silly, but at least it explains the striped pattern that results from Young’s experiment performed with individual photons. In comparison, the old-fashioned classical view is that the photon must have passed through one of the two slits, and we simply do not know which one—this seems much more sensible than the quantum view, but unfortunately it cannot explain the observed result.
Erwin Schrödinger, who won the Nobel Prize for Physics in 1933, invented a parable known as “Schrödinger’s cat,” which is often used to help explain the concept of superposition. Imagine a cat in a box. There are two possible states for the cat, namely dead or alive. Initially, we know that the cat is definitely in one particular state, because we can see that it is alive. At this point, the cat is not in a superposition of states. Next, we place a vial of cyanide in the box along with the cat and close the lid. We now enter a period of ignorance, because we cannot see or measure the state of the cat. Is it still alive, or has it trodden on the vial of cyanide and died? Traditionally we would say that the cat is either dead or alive, we just do not know which. However, quantum theory says that the cat is in a superposition of two states—it is both dead and alive, it satisfies all possibilities. Superposition occurs only when we lose sight of an object, and it is a way of describing an object during a period of ambiguity. When we eventually open the box, we can see whether the cat is alive or dead. The act of looking at the cat forces it to be in one particular state, and at that very moment the superposition disappears.
For readers who feel uncomfortable with superposition, there is the second quantum camp, who favor a different interpretation of Young’s experiment. Unfortunately, this alternative view is equally bizarre. The
many-worlds interpretation
claims that upon leaving the filament the photon has two choices-either it passes through the left slit or the right slit—at which point the universe divides into two universes, and in one universe the photon goes through the left slit, and in the other universe the photon goes through the right slit. These two universes somehow interfere with each other, which accounts for the striped pattern. Followers of the many-worlds interpretation believe that whenever an object has the potential to enter one of several possible states, the universe splits into many universes, so that each potential is fulfilled in a different universe. This proliferation of universes is referred to as the
multiverse
.
Whether we adopt superposition or the many-worlds interpretation, quantum theory is a perplexing philosophy. Nevertheless, it has shown itself to be the most successful and practical scientific theory ever conceived. Besides its unique capacity to explain the result of Young’s experiment, quantum theory successfully explains many other phenomena. Only quantum theory allows physicists to calculate the consequences of nuclear reactions in power stations; only quantum theory can explain the wonders of DNA; only quantum theory explains how the sun shines; only quantum theory can be used to design the laser that reads the CDs in your stereo. Thus, like it or not, we live in a quantum world.
Of all the consequences of quantum theory, the most technologically important is potentially the quantum computer. As well as destroying the security of all modern ciphers, the quantum computer would herald a new era of computing power. One of the pioneers of quantum computing is David Deutsch, a British physicist who began working on the concept in 1984, when he attended a conference on the theory of computation. While listening to a lecture at the conference, Deutsch spotted something that had previously been overlooked. The tacit assumption was that all computers essentially operated according to the laws of classical physics, but Deutsch was convinced that computers ought to obey the laws of quantum physics instead, because quantum laws are more fundamental.