The Dancing Wu Li Masters (21 page)

Einstein’s revolutionary insight was that events which are simultaneous for one observer may occur at different times for another observer depending upon their relative motion. Put another way, two
events, one of which occurs before the other as seen from the frame of reference of one observer, may occur at the same time when seen from the frame of reference of another observer. One observer uses the words “sooner” and “later.” The other observer uses the word “simultaneous,” even though both of them are describing the same two events.

In other words, “sooner,” “later,” and “simultaneous” are local terms. They have no meaning in the universe at large unless they are tied down to a specific frame of reference. What is “sooner” in one frame of reference may be “later” in another frame of reference and “simultaneous” in a third.
^*

The mathematics which translate what an observer in one frame of reference sees into what an observer in another frame of reference sees are the Lorentz transformations. Einstein adopted the Lorentz transformations—which are a set of equations—virtually intact.

No one before Einstein got these startling results from this simple type of thought experiment because no one before Einstein had the audacity to postulate something as outrageous as the principle of the constancy of the velocity of light. No one had the audacity to postulate something as outrageous as the principle of the constancy of the velocity of light because the principle of the constancy of the velocity of light completely and unequivocally contradicts common sense; specifically, common sense as represented by the classical transformation laws. The classical transformation laws are so embedded in our everyday experience that it simply never occurred to anybody to question them.

Even when the Michelson-Morley experiment produced results that were incompatible with the classical transformation laws, no beginner’s mind but Einstein’s conceived that the classical transformation laws might be wrong. Only Einstein suspected that at very high velocities, velocities far faster than those that we encounter through
our senses, the classical transformation laws do not apply. This is not to say that they are incorrect. At low velocities (compared to 186,000 miles per second) contraction and time dilation are not detectable sensorily. In this limited situation, the classical transformations are a good guide for practical experience. After all, we do reach the top of an escalator faster if we walk.

If we do the moving-room experiment with sound instead of light, we do not get the special theory of relativity. We get a confirmation of the classical transformation laws. There is no principle of the constancy of the velocity of sound because the velocity of sound is not constant. It varies depending upon the motion of the observer (hearer) as dictated by common sense. The important word here is “dictated.”

We live out our lives in a limited situation of low velocities where the speed of sound (about 700 miles per hour) seems “fast.” Therefore, our common sense is based upon our experiences in this limited environment. If we want to expand our understanding beyond the limitations of this environment, it is necessary to drastically rearrange our conceptual constructs. This is what Einstein did. He was the first person to see that this is what had to be done in order to make sense of such impossible experimental findings as the constancy of the velocity of light for each and every person who measures it, regardless of their states of motion.

This led him to turn the puzzle of the constancy of the velocity of light into the principle of the constancy of the velocity of light. In turn, that led him to the conclusion that, if the velocity of light really is constant for all observers, then the measuring instruments used by different observers in different states of motion somehow must vary so that all of them give the same result. By a stroke of luck, Einstein discovered that these same variances were expressed in the equations of the Dutch physicist Hendrik Lorentz, and so he borrowed them. Lastly, the fact that moving clocks change their rhythm led Einstein to the inescapable conclusion that “now,” “sooner,” “later,” and “simultaneous” are
relative
terms. They all depend upon the state of motion of the observer.

This conclusion is precisely the opposite of the assumption upon which Newtonian physics is based. Newton assumed, as did we all, that there is one clock ticking off the seconds by which the entire universe grows older. For every second of time that passes in this corner of the universe, one second of time passes also in every other corner of the universe.

According to Einstein, this is incorrect. How can anyone say when it is “now” throughout the universe? If we try to designate “now” by the occurrence of two simultaneous events (like my arrival at the doctor’s office and my watch indicating 3 o’clock), we find that an observer in another frame of reference sees one of our events happening before the other. Absolute time, wrote Newton, “flows equably…,”
⁷
but he was wrong. There is no single time which flows equally for all observers. There is no absolute time.

The existence of one ultimate flow of time throughout the physical universe, which we all tacitly acknowledged, turned out to be another piece of clothing that the Emperor wasn’t wearing.

Newton made one more mistake in this regard. He said that time and space were separate. According to Einstein, time and space are not separate. Something cannot exist at some place without existing at some time, and neither can it exist at some time without existing at some place.

Most of us think of space and time as separate because that is the way that we think that we experience them. For example, we seem to have some control over our position in space, but none at all over our position in time. There is nothing that we can do about the flow of time. We can choose to stand perfectly still, in which case our position in space does not change, but there is no way that we can stand still in time.

This notwithstanding, there is something very elusive about “space” and especially about “time”; something that prevents us from “resting our accounts with them prematurely.” Subjectively, time has a fluid quality which much resembles a running brook; sometimes bubbling past in a furious rush, sometimes slipping by quietly
unnoticed, and sometimes lying languid, almost stationary, in deep pools. Space, too, has an ubiquitous quality about it which belies the common notion that it serves only to separate things.

William Blake’s famous poem reaches out toward these intangible qualities:

(Its title, by no coincidence is “Auguries of Innocence.”)

The special theory of relativity is a physical theory. Its concern is with the mathematically calculable nature of reality. It is
not
a theory of subjectivity. Although it shows that the appearances of physical reality may vary from one frame of reference to another, it is a theory about the unchanging (physicists say “invariant”) aspect of physical reality. Nonetheless, the special theory of relativity was the first mathematically rigorous physical theory to explore areas whose expression previously had been the domain of poets. Like any concise and poignant
re-presentation
of reality, the theories of relativity
are
poetry to mathematicians and physicists. However, Albert Einstein’s enormous public renown perhaps was due in part to a shared intuition that he had something profoundly relevant to say about space and time.

What Einstein had to say about space and time is that there is no such thing as space
and
time; there is only space-time. Space-time is a continuum. A continuum is something whose parts are so close together, so “arbitrarily small,” that the continuum really cannot be broken down into them. There are no breaks in a continuum. It is called a continuum because it flows continuously.

For example, a one-dimensional continuum is a line drawn on a wall. Theoretically we might say that the line is comprised of a series of points, but the points are each infinitely close to one another. The result is that the line flows continuously from one end of it to the other.

An example of a two-dimensional continuum is the wall. It has
two dimensions, length and width. Similarly, all of the points on the wall are in contact with other points on the wall, and the wall itself is a continuous surface.

A three-dimensional continuum is what we commonly call “space.” A pilot flying his airplane navigates in a three-dimensional continuum. To give his location he must state, for example, not only how far north and how far east of a given point he is, but he also must report his altitude. The airplane itself, like all things physical, is three-dimensional. It has a width, a height, and a depth. This is why mathematicians call our reality (their reality, too) three-dimensional.

According to Newtonian physics, our three-dimensional reality is separate from, and moves forward in, a one-dimensional time. Not so, says the special theory of relativity. Our reality is
four-dimensional
, and the fourth dimension is time. We live, breathe, and exist in a four-dimensional space-time continuum.

The Newtonian view of space and time is a
dynamic
picture. Events
develop
with the passage of time. Time is one-dimensional and
moves
(forward). The past, present, and future happen in that order. The special theory of relativity, however, says that it is preferable, and more useful, to think in terms of a
static
, nonmoving picture of space and time. This is the space-time continuum. In this static picture, the space-time continuum, events do not develop, they just are. If we could view our reality in a four-dimensional way, we would see that everything that now seems to unfold before us with the passing of time, already exists
in toto
, painted, as it were, on the fabric of space-time. We would see all, the past, the present, and the future with one glance. Of course, this is only a mathematical proposition (isn’t it?).

Don’t worry about visualizing a four-dimensional world. Physicists can’t do it, either. For the moment, just assume that Einstein might be right since the evidence so far suggests that he is. His message is that space and time are related in an intimate manner. For lack of a better way of saying it, he expressed this relationship by calling time a fourth dimension.

“Fourth dimension” is a translation from one language to another. The original language is mathematics and the second lan
guage is English. The problem is that there is simply no way of precisely expressing what the first language says in terms of the second language. Therefore, “time as a fourth dimension” is merely a label that we give to a
relationship
. The relationship in question is the relationship between space and time as it is expressed mathematically in the theories of relativity.

The relationship between space and time that Einstein discovered is similar to the relationship between the sides of a right triangle which Pythagoras the Greek (a contemporary of Confucius) discovered about 550
B.C.

A right triangle is a triangle that contains a right angle. A right angle is formed whenever two perpendicular lines intersect. Below is a right triangle. The side of a right triangle that is opposite the right angle is called the hypotenuse
. The hypotenuse is always the longest side of a right triangle.

Pythagoras discovered that as long as we know the length of the two shorter sides of a right triangle, we can calculate the length of the longest side. This relationship, expressed mathematically, is the Pythagorean theorem: The first leg squared plus the second leg squared equals the hypotenuse squared.

A hypotenuse of a given length can be calculated from many different combinations of shorter legs. In other words, there are many combinations of different-size legs that all calculate to have the same hypotenuse.

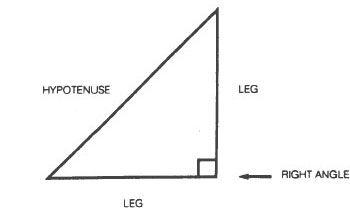
For example, the first leg might be very short and the second leg very long.