The Dancing Wu Li Masters (31 page)

For example, because the arrowheads distinguish the particles from the anti-particles, we can twist the original Feynman diagram around into any position that we choose and still be able to distinguish the one from the other. Here are some different ways that we can twist the original Feynman diagram.

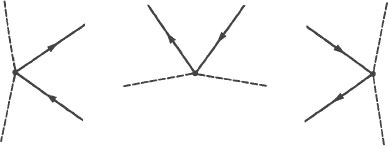
Each of these variations is a separate diagram and represents a particle/anti-particle interaction.
^*
By twisting the original diagram completely around we can represent every possible interaction between an electron, a positron, and two photons. The precision, simplicity, and symmetry of Feynman diagrams make them a special type of poetry.

On the next page is a space-time diagram of
two events
. A collision between two photons (at B) creates an electron-positron pair and, subse
quently, an electron and a positron annihilate each other and create two photons (at A). (The left half of this diagram, the interaction at A, is the same as the electron-positron annihilation.

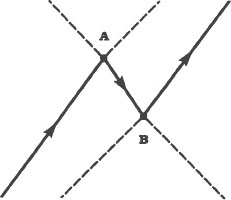
Ordinarily we would interpret these events as follows: Two photons collide in the lower right of the diagram producing an electron-positron pair. The electron flies off to the right while the positron flies off to the left where it meets another electron which has entered the diagram from the lower left. There they mutually annihilate and create two photons which depart in opposite directions.

The preferred interpretation of quantum field theory, however, is much simpler. In it there is only
one
particle. That particle, an electron, enters the diagram from the lower left and travels forward in time and space until it emits two photons at A. This causes it to reverse its direction in time. Traveling backward in time as a positron it absorbs two photons at B, reverses its direction in time again, and again becomes an electron. Instead of three particles there is only one particle which, moving from left to right, travels first forward in time, then backward in time, and then forward in time again.

This is the static type of space-time picture described in Einstein’s theory of relativity. If we could survey an entire span of time as we can survey an entire region of space, we would see that events do not unfold with the flow of time but present themselves complete, like a finished painting on the fabric of space-time. In such
a picture movements backward and forward in time are no more significant than movements backward and forward in space.

The illusion of events “developing” in time is due to our particular type of awareness which allows us to see only narrow strips of the total space-time picture one at a time. For example, suppose that we place a piece of cardboard with a narrow strip cut out of it over the diagram so that all we can see of the interaction is what is visible through the cut-out. If we move the cardboard slowly upward, starting at the bottom, our restricted view discovers a series of events, each one happening after the other.

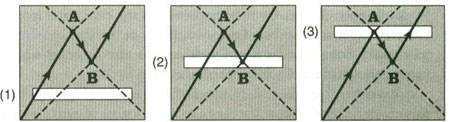
First, we see three particles, two photons entering our view on the right and an electron entering from the left (1). Next, we see the photons collide to produce an electron-positron pair, the electron flying off to the right and the positron flying off to the left (2). Finally, we see the newly created positron meet the original electron to create two new photons (3). Only when we remove the entire cardboard (which was an artificial construction anyway) can we see the complete picture.

“In space-time,” wrote de Broglie,

“Wait a minute,” says Jim de Wit to a passing particle physicist. “It is easy to talk of movement backward and forward in time, but I
never have experienced going backward in time. If particles can travel backward in time, why can’t
I
travel backward in time?”

The answer which physicists gave to this question is actually quite simple: There is a growing tendency in any closed part of the universe, their explanation goes, for disorder (called “entropy”) to expand at the price of order (called “negentropy”). Suppose, for example, that we deposit a drop of black ink into a glass of clear water. Initially its presence is quite ordered. That is, all of the molecules of ink are located in one small area and are clearly segregated from the molecules of clear water.

As time passes, however, natural molecular motion will cause the black ink molecules steadily to intersperse with the clear water molecules until they are distributed evenly throughout the glass, resulting in a murky homogeneous liquid with no structure or order whatever—only a bland uniformity (maximal entropy).

Experience has taught us to associate increasing entropy with the forward movement of time. If we see a movie of a glass of murky water becoming clearer and clearer until all of the foreign substance in it collects into one small drop at the top, we know at once that the film is running backward. Of course, it is theoretically possible for this to happen, but it is so improbable that it simply never (probably) will happen. In short, time “flows” in the direction of high probability, which is the direction of increasing entropy.

The theory of growing disorder, or “increasing entropy,” is called the second law of thermodynamics. The second law of thermodynamics is statistical. That means it won’t work unless there are many entities in a given situation to apply it to. Generally speaking, individual subatomic particles are conceived as such conceptually isolated, short-lived entities that the second law of thermodynamics does not apply to them.
^*
,
^†
It does apply, however, to molecules, which are
quite complex compared to subatomic particles; to living cells, which are more complex than molecules; and to people, who are made of billions of cells. It is only at the subatomic, or quantum, level that the forward flow of time loses its significance.

However, there is speculation, and some evidence, that consciousness, at the most fundamental levels,
is
a quantum process. The dark-adapted eye, for example, can detect a single photon. If this is so then it is conceivable that by expanding our awareness to include functions which normally lie beyond its parameters (the way yogis control their body temperature and pulse rate) we can become aware of (experience) these processes themselves.
If
, at the quantum level, the flow of time has no meaning, and
if
consciousness is fundamentally a similar process, and
if
we can become aware of these processes within ourselves, then it also is conceivable that we can experience timelessness.

If we can experience the most fundamental functions of our psyche, and if they are quantum in nature, then it is possible that the ordinary conceptions of space and time might not apply to them at all (as they don’t seem to apply in dreams). Such an experience would be difficult to describe rationally (“Infinity in a grain of sand/And eternity in an hour”), but it would be very real, indeed. For this reason, reports of time distortion and timelessness from gurus in the East and psychotropic drug users in the West ought not, perhaps, to be discarded preemptorily.

Subatomic particles do not just sit around being subatomic particles. They are beehives of activity. An electron, for example, constantly is emitting and absorbing photons. These photons are not full-fledged photons, however. They are a now-you-see-it-now-you-don’t variety. They are exactly like real photons except that they don’t fly off on their own. They are re-absorbed by the electron almost as soon as they are emitted. Therefore, they are called “virtual” photons. (“Virtual” means “being so in effect or essence, although not in actual fact.”) They are virtually photons. The only thing that keeps them from
being full-fledged photons is their abrupt re-absorption by the electron that emits them.
^*

In other words, first there is an electron, then there is an electron and a photon, and then there is an electron again. This situation is, of course, a violation of the conservation law of mass-energy. The conservation law of mass-energy says, in effect, that we cannot get something for nothing. According to quantum field theory, however, we do get something for nothing, but only for about one thousand trillionth (10
^-15
) of a second.
^†
The reason that this can happen, according to the theory, is the famous Heisenberg uncertainty principle.

The Heisenberg uncertainty principle, as it originally was formulated, says that the more certain we are of the position of a particle, the less certain we can be about its momentum, and the other way round. We can determine its position precisely, but in that case we cannot determine its momentum at all. If we choose to measure its momentum precisely, then we will not be able to know where it is located.

In addition to the reciprocal uncertainty of position and momentum, there also is a reciprocal uncertainty of time and energy. The less uncertainty there is about the time involved in a subatomic event, the more uncertainty there is about the energy involved in the event (and the other way round). A measurement as accurate as one thousand trillionth of a second leaves very little uncertainty about the time involved in the emission and absorption of a virtual photon. It does, however, cause a specific uncertainty about how much energy was involved. Because of this uncertainty, the balance books kept by the
conservation law of mass-energy are not upset. Said another way, the event happens and is over with so quickly that the electron can get away with it.

It is as if the policeman who enforces the conservation law of mass-energy turns his back on violations if they happen quickly enough. However, the more flagrant the violation, the more quickly it must happen.

If we provide the necessary energy for a virtual photon to become a real photon without violating the conservation law of mass-energy, it does just that. That is why an excited electron emits a real photon. An excited electron is an electron that is in an energy level higher than its ground state. An electron’s ground state is its lowest energy level where it is as close to the nucleus of an atom as it can get. The only photons that electrons emit when they are in their ground state are virtual photons which they immediately re-absorb so as not to violate the conservation law of mass-energy.

An electron considers the ground state to be its home. It doesn’t like to leave home. In fact, the only time it leaves its ground state is when it literally is pushed out of it with extra energy. In that case, the electron’s first concern is to get back to its ground state (provided that it hasn’t been pushed so far from the nucleus that, in effect, it becomes a free electron). Since the ground state is a low-energy state, the electron must lose its excess energy before it can return to it. Therefore, when an electron is at an energy level higher than its ground state, it jettisons its excess energy in the form of a photon. The jettisoned photon is one of the electron’s virtual photons that suddenly finds itself with enough energy to keep going without violating the conservation law of mass-energy, and it does. In other words, one of the electron’s virtual photons suddenly is “promoted” to a real photon. The amount of energy (the frequency) of the promoted photon depends upon how much excess energy the electron had to jettison. (The discovery that electrons emit only photons of certain energies and no others is what made the quantum theory a
quantum
theory). Electrons are always surrounded by a swarm of virtual photons.
^*