The Eternal Flame (14 page)
Authors: Greg Egan
Tags: #Science Fiction, #General, #Space Opera, #Fiction

“Maybe some energy leaks out of these valleys as heat,” Patrizia suggested. “Then it takes time to make up for that.”
“Make up for it how?”
“With a longer exposure.”
“But all you can
do
with a longer exposure is create more photons!” Carla protested. “And if the numbers of photons aren’t what I’ve drawn here, where does the five-to-four ratio in the frequencies come from?”
Patrizia hummed in self-reproach. “Of course. I’m not thinking straight.”
Carla saw Onesto glance up from his papers. He’d endured the jarring lighting for six days, and now he had to listen to the two of them stumbling around trying to make sense of their non-result. “I’m sorry if we’re disturbing you,” she said.
“You’re not disturbing me,” Onesto replied. “But to be honest, I haven’t been able to get much work done for the last two bells.”
“Why not?”
“Something’s been puzzling me about your theory,” he said, “and the more I see you puzzled yourselves, the more I’m tempted to break my silence. So if it’s not too discourteous, I hope you’ll let me speak my mind.”
Carla said, “Of course.”
Onesto approached. “Nereo posited a particle, the luxagen, to act as a source for Yalda’s light field. If I’ve understood what you’re saying, you’re now positing an entirely new particle that plays a very different role: traveling with the waves in the field itself, carrying their energy for them.”
Carla turned to Patrizia; the theory was hers to define and defend. Patrizia said, “That’s right.”
“Then why not complete the pattern?” Onesto suggested. “If you have reason to believe that the light field can manifest as a particle, why should Nereo’s own particle be different? Shouldn’t
the luxagen
be associated with waves in a field of its own?”
Patrizia looked confused, so Carla stepped in.
“There would be an appealing symmetry to that,” she said. “To every wave, its particle; to every particle, its wave. But I think it would complicate the theory unnecessarily. Without any evidence for a ‘luxagen field’, it’s hard to see what could be gained by including it.”
Onesto inclined his head politely. “Thank you for listening. I’ll leave you in peace now.”
He was halfway to his desk when Patrizia said, “You want us to treat the luxagen as a standing wave?”
Onesto turned. “I wasn’t thinking of anything so specific,” he admitted. “It just seems odd to treat the two particles so differently.”
At this response Patrizia’s confidence wavered, but then she persisted with her line of thought. “Suppose the luxagen follows the same kind of rules as the photon,” she said. “It has its own waves—and just like light waves, their frequency is proportional to the particle’s energy.”
Carla said, “All right. But…”
“If the luxagen is trapped in an energy valley,” Patrizia said, “its wave must be trapped as well. A trapped wave, a standing wave, can only take on certain shapes—each one with a different number of peaks.”
Carla felt the scowl vanish from her face. Unlike Patrizia’s last suggestion, this wasn’t hunger-addled nonsense. Onesto’s proposal had sounded naïve—but now Carla could see where her infuriating, erratically brilliant student was taking it.
For each shape it could adopt, the luxagen’s standing wave would oscillate with a specific frequency. The same kind of principle governed the harmonics of a drum: the geometry of the resonant modes of the drumhead dictated the particular sounds it could make, each one with its characteristic pitch.
But Patrizia’s rule linked frequencies to energies—so a trapped luxagen would only be able to possess certain
energies
. The energy closest to the top of the valley would set the gap that needed to be jumped in order for tarnishing to occur, and there would be no doing it by halves: a luxagen couldn’t accumulate five photons’ worth of energy and then wait around for a sixth. Once you reached the highest energy level there were no more resting places; it was an all-or-nothing trip. You either made the total number of photons you needed,
all at once
, and escaped the valley… or you didn’t.
As they talked it over, Patrizia sketched the general idea. Onesto looked on, pleased that his suggestion had proved helpful but a little daunted by the strange outcome.
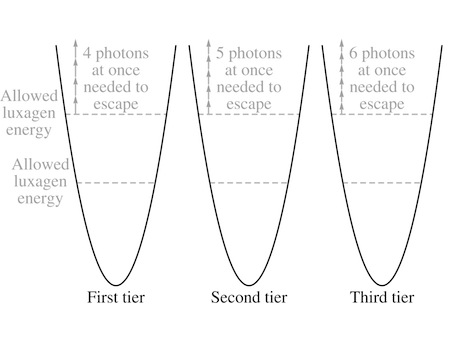
“I still don’t understand the details of the timing,” Carla confessed, “but if you don’t get to make the photons separately, one by one, there’s no reason to expect the time it takes to be proportional to the number of photons.”
“Can we quantify any of this?” Patrizia asked.
Carla said, “We could try to write an equation for the luxagen wave. Whatever we know about the luxagen’s energy, we translate into the wave’s frequency; whatever we know about the luxagen’s momentum, we translate into the wave’s
spatial frequency
.”
The idea seemed straightforward, but they struck a problem almost at once. Taking the rate of change of an oscillating wave multiplied it by a factor proportional to its frequency, but also shifted the wave by a quarter-cycle: at every peak of the original wave the rate of change crossed zero, heading downwards, while at every such zero of the original wave the rate of change was at a minimum, the bottom of a trough. When Yalda had devised her light equation she had been able to go one step further: the
second
rate of change was shifted by another quarter-cycle, putting it a half-cycle away from the original—yielding the original wave turned upside down and multiplied by the frequency squared.
Multiples of the original wave were easy to combine. The geometrical relationship Yalda had sought to express—that the sum of the squares of the wave’s frequencies in all four dimensions was a constant—could be encoded in the wave equation simply by multiplying every term in that relationship by the strength of the wave, then re-expressing the squared frequencies as second rates of change.
But with a luxagen in a solid, the relationship between its energy and momentum included its potential energy, which depended on its position in the energy valley. It was impossible to write this relationship purely in terms of the energy
squared
—so it was impossible to talk only of frequencies
squared
. To go halfway and include the frequency itself meant taking the square root of the operation that turned the wave upside down—putting the square root of minus one into the wave equation.
“It looks as if we’re stuck with complex numbers,” Carla declared. “What does
that
mean? That our premises are wrong?”
Patrizia seemed to share her sense of trepidation, but she wasn’t ready to give up. “Let’s follow the mathematics,” she suggested. “We should see what the final answers are before deciding whether or not it all makes sense.”
To make the calculations easier they chose a field described by a single number—albeit complex—rather than a vector like light, with its different polarizations. They also assumed that the luxagen would be moving slowly. For a parabolic energy valley—the easiest idealization to work with—it was possible to solve the equation exactly.
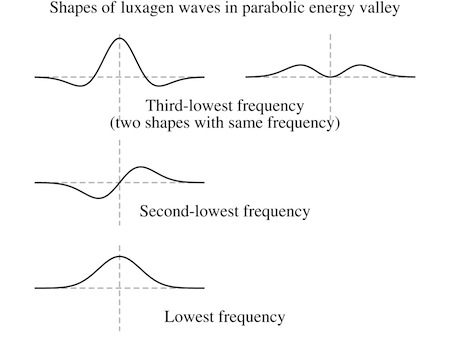
As Patrizia had guessed from the start, there was a sequence of solutions with distinct shapes. Those shapes could be described with real numbers alone, though the wave’s variation over time swept out a circle in the complex number plane with a frequency corresponding to its energy.
Some solutions shared the same energy, though that was just a consequence of the idealized shape of the valley. Carla pushed on further and managed to calculate the effect of switching to a more realistic valley, closer to the kind that was actually produced by Nereo’s force in a solid.
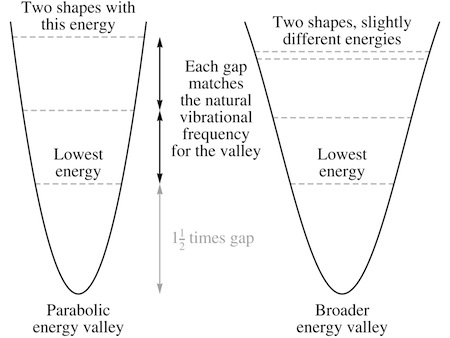
For the parabolic case all the energies were governed by the natural frequency at which a luxagen—as a particle—would be expected to vibrate in such a valley. The gaps between the allowed energies all corresponded precisely to that frequency, while the lowest energy sat one and a half times higher above the valley floor. For a more realistic valley, all the energies were reduced slightly, and the perfect agreement between the multiple higher-energy solutions broke down, splitting the idealized single energy levels into closely spaced sets.
Onesto said, “Suppose the natural frequency for the valley is greater than the maximum frequency of light. That’s the assumption at the core of the original theory of solids. But what does it mean, in your terms?”
Carla thought for a moment. “It means the energy gap exceeds the mass of a photon—so creating a single photon can never give you enough energy to jump the gap.”
“And if the valley’s not a perfect parabola,” Onesto observed, “that doesn’t really change the significance of the main energy gaps, does it? There’ll be smaller gaps as well, but if the main ones are large enough there’ll still be energy levels where you need to make more than one photon in order to rise any higher.”
“Right,” Carla said. “And if the valley is deep enough, those gaps could end up so large that you’d need to make six or seven photons to cross them.”
Patrizia turned to Carla. “Doesn’t that… solve the stability problem?”
Carla considered the question seriously. In the old way of looking at the problem, even if the walls of the energy valley were so steep that the luxagen rolled back and forth at a rate dozens of times greater than the maximum frequency of light, the tiniest deviation from a parabolic shape would introduce lower-frequency components into its motion—some of them low enough to produce light. And however feeble the radiation emitted that way, the luxagen would slowly gain energy and creep up the valley, until it finally escaped.
But that was in a world where energies could take on any value at all. In the new theory of luxagens as waves, a steep enough valley would have gaps between its energy levels that were insurmountable—and the inevitable imperfections in the shape of the valley would merely split some of those levels. As Onesto had pointed out, if the rungs of the original energy ladder were spaced sufficiently widely, adding a few extra rungs close to the originals wouldn’t suddenly make the whole thing traversable. The valley’s imperfection no longer undermined its stability.
“We still don’t know how long it takes to create a given number of photons,” Carla said cautiously. “But we do know that it takes much longer to make five than four, and a great deal longer to make six—even with the beam from a sunstone lamp to help. If we could understand what was going on there, I think we’d be getting close to explaining how some solids can be stable.”
Patrizia sketched the shapes of the first few luxagen waves on her own chest. “What happens if I add two of these solutions together—two waves with different energies? The sum will still solve the same equation… so what does the combined wave represent? Two luxagens, one with each energy?”
Carla said, “That doesn’t sound right. We found the wave equation by translating the energy-momentum relationship for a single particle. And what if I add two solutions in unequal proportions? Say, one quarter the first solution and three quarters the other?”
“Couldn’t that be… one particle with the first energy, and three with the second?” Patrizia didn’t sound too persuaded herself; she could probably see where this numbers game was heading.