The Particle at the End of the Universe: How the Hunt for the Higgs Boson Leads Us to the Edge of a New World (40 page)

This is a good-news/bad-news situation. The bad news is that science is hard. Nature is unforgiving, and most theories one can imagine proposing (and indeed, the vast proportion of theories that actually are proposed) will turn out to be incorrect. But the good news is that nature, that strict taskmaster, gradually guides us to ideas we never would have invented through pure thought alone. To paraphrase Sidney Coleman, a thousand philosophers thinking for a thousand years would never have invented anything as strange as quantum mechanics. It’s only because the data force us into corners that we are inspired to create the highly counterintuitive structures that form the basis for modern physics.

Imagine that a person in the ancient world was wondering what made the sun shine. It’s not really credible to imagine that they would think about it for a while and decide, “I bet most of the sun is made of particles that can bump into one another and stick together, with one of them converting into a different kind of particle by emitting yet a third particle, which would be massless if it wasn’t for the existence of a field that fills space and breaks the symmetry that is responsible for the associated force, and that fusion of the original two particles releases energy, which we ultimately see as sunlight.” But that’s exactly what happens. It took many decades to put this story together, and it never would have happened if our hands weren’t forced by demands of observation and experiment at every step.

The flip side is that once the data put us on the right track, science is capable of extraordinary leaps into the future. In the 1960s, physicists constructed a unified theory of the electromagnetic and weak interactions, based on some general principles that previous experiments had validated and some specific observational facts, such as the absence of massless weak-force-carrying bosons. That theory made a prediction: There should be a new massive particle, the Higgs boson, that couples to the known particles in certain definite ways. In 2012, a full forty-five years after Steven Weinberg’s 1967 paper put the theory together, that prediction came true. The human intellect, guided by nature’s clues, was able to figure out a deep truth about how the universe works. And on the basis of that insight we hope to see even further in the years to come.

When I talked with JoAnne Hewett about what makes a successful physicist, one word kept recurring: “persistence.” Individual scientists require persistence to stick with tough problems, and society as a whole needs to be willing to support costly long-term projects to tackle our hardest questions. When it comes to understanding the architecture of reality, the low-hanging fruit has been picked. The easy part is over.

The questions we are faced with are difficult ones, but if recent history is any guide, a combination of dogged effort and occasional flashes of insight should be able to get us there. The construction of the Standard Model may be complete, but the task of incorporating the rest of reality into human understanding remains before us. If it weren’t a challenge, it wouldn’t be so much fun.

APPENDIX ONE

MASS AND SPIN

The first thing we say about the Higgs field is that it gives mass to other particles. In this appendix, we’re going to explain what that means, somewhat more carefully than we do in the main text. Nothing here is absolutely necessary, but it may clarify a thing or two.

So: Why do we
need
a field whose job it is to give mass to other particles? Why can’t the particles just have mass without any help?

We can certainly imagine massive particles without the Higgs field being involved at all. But the particles of the Standard Model are of a special type that doesn’t allow for that to happen. There are two different sets of particles that get mass from the Higgs field: the force-carrying W and Z bosons of the weak interactions, and the electrically charged fermions (electron, muon, tau, and all the quarks). The way the bosons get masses is different in detail from the way the fermions get masses, but the underlying motto is the same in both cases: There is a symmetry that seems to prohibit any mass at all, and the Higgs field breaks that symmetry. To understand how that happens, we need to talk about the
spin
of elementary particles, which we’ve been skirting around thus far in the book.

Spin is one of the fundamental defining features of a particle in quantum mechanics. The phrase “quantum mechanics” itself, although not the most accurate terminology ever invented, stems from the fact that certain things come only in discrete packets, not in any possible amount. For example, the energy of an electron that is bound to an atomic nucleus is only allowed to take on certain specific values. The same is true for a quantity known as the “angular momentum,” which is a way of characterizing how fast one object is rotating or moving around another object. The rules of quantum mechanics tell us that angular momentum is quantized: It can come only in fixed multiples of a fundamental value. The minimum unit of angular momentum is given by Planck’s constant
h
, a fundamental quantity of nature, divided by two pi. This quantity is so important that it gets its own funky orthography, and is called
h
^-
, pronounced “
h
-bar.” Planck invented his original constant
h
back in the earliest days of quantum mechanics, but it turns out that
h
^-
is much more useful, so we often simply call that “Planck’s constant.” Numerically,
h
^-
is equal to about 6.58 × 10
^-16
, in units of electron volts times seconds.

Imagine you have a spinning top that you can manipulate very precisely. You make it spin more and more slowly, and observe what it’s doing as accurately as you please. What you will find is that as you slow the top down, only discrete rotational speeds are allowed; the rotation of the top will suddenly change from one speed to another, like the second hand on a quartz watch suddenly hopping from one second to the next. Eventually you will hit a slowest-possible rotation, when the total angular momentum of the top is equal to
h
^-
. The reason why you don’t notice this when you are watching Olympic skaters spinning on the ice is that the minimum rotation is very slow: A toy top with angular momentum
h
^-
would take a hundred trillion times the age of the universe to complete a full turn.

The spin of a top has angular momentum because the atoms in the top are literally rotating around some central axis. One of the consequences of quantum mechanics is that individual particles can also have “spin,” even though they’re not really rotating around anything. The way we know that is because total angular momentum stays constant through time, and we see processes where orbiting particles interact and get turned into particles that aren’t orbiting at all. In this case we can conclude that the angular momentum must have gone into the spin of the particle. When we say “spin,” we’ll always mean this intrinsic quantum-mechanical spin of elementary particles, and when we say “angular momentum,” we’ll be thinking of the classical phenomenon of one object moving around another one (also known as “orbital” angular momentum).

How spin works

There are a few crucial facts we need to know about particle spin. Every kind of particle has a fixed amount of spin once and for all; they never start spinning faster or slower. Measured in units of
h
^-
, every photon in the universe has a spin equal to one, and every Higgs boson has a spin equal to zero. Spin is an intrinsic feature of the particle, not something that changes as the particle evolves (unless it transforms into another kind of particle).

Unlike regular orbital angular momentum, the smallest unit of spin is one-half
h
^-
, rather than
h
^-
itself. An electron has a spin of one-half, as does an up quark. Why this is possible is an amusing quirk of quantum field theory, but delving into it would take us even further afield than the rest of this relatively technical appendix.

There is a simple correlation between the spin of a particle and its nature as a boson or fermion. Every boson has a spin that is an integer: 0, 1, 2, etc. (in units of
h
^-
, which we will assume henceforth). Every fermion has a spin that is an integer plus a half: 1/2, 3/2, 5/2, etc. This connection is so close that people often define bosons as “particles with integer spin” and fermions as “particles with half-integer spin.” That’s not really right; the definition we gave, that bosons can pile on top of one another while fermions take up space, is the true distinction between these two classes of particles. A famous theorem in physics, the “spin-statistics theorem,” tells us that particles that can pile on top of one another must have integer spins, and particles that take up space have half-integer spins. At least in a four-dimensional spacetime—but that’s all we care about here.

The particles of the Standard Model have very specific spins. All of the known elementary fermions—quarks, charged leptons, and neutrinos—are spin-1/2. The gravitino, hypothetical supersymmetric partner of the graviton, would be spin-3/2, but no gravitinos have ever been observed. The graviton itself is spin-2, uniquely among the elementary particles. The other gauge bosons—the photon, gluons, and the Ws and Z—are all spin-1. (The difference between the graviton and the other force-carrying bosons is ultimately traced to the fact that the symmetry underlying gravity is a symmetry of spacetime itself, while the other forces propagate on top of spacetime.) The Higgs boson, standing apart from all the rest, is spin-0. Particles with zero spin are called “scalars,” and the fields from which they arise are called “scalar fields.”

It’s important to distinguish between the “spin of a particle” and the “value of the spin we measure with respect to some axis.” Suppose the angular momentum of the earth spinning on its axis, pointing from the South Pole to the North Pole, is some (large) number. Then we say that we could imagine measuring the angular momentum with respect to an axis pointing in the opposite direction, from north to south. This answer would be minus the original right-side-up answer. The angular momentum hasn’t changed, we’ve just measured it with respect to a different axis. If we look at the original axis from above, a positive spin means we see the object rotating counterclockwise, while a negative spin means it’s rotating clockwise. The earth spins counterclockwise from the perspective of someone looking down from the North Pole, so it has a positive spin. (This is known as the “right-hand rule”—if you curl the fingers of your right hand in the direction something is spinning, your thumb points to the axis along which that spin is positive.)

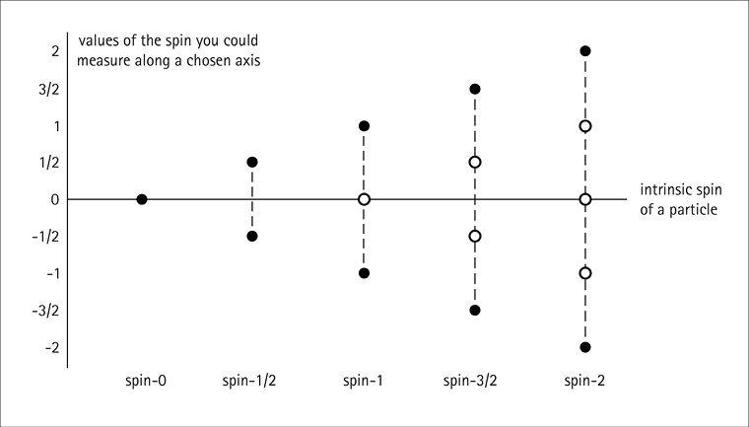
Allowed outcomes of measuring the intrinsic spin of a particle with respect to some axis. Massless particles give only the answers corresponding to filled circles, while massive particles give answers corresponding to both filled and open circles.

We can even consider measuring the angular momentum with respect to a completely perpendicular axis—say, one pointing from one side of the equator to the other. With respect to that direction, the earth isn’t “spinning” at all—the North and South Poles stay in the same position with respect to an imaginary axis passing through the equator. So we would say that the spin measured with respect to that axis is zero.

Just as the total spin of a particle is quantized to be some integer or half-integer multiple of
h
^-
, the spin you can measure is also quantized. It must either be equal to the total spin, or minus the total spin, or some number in between separated by integers. For a spin-0 particle, the only possible answer we can get while measuring the spin is 0. For a spin-1/2 particle, we could get +1/2 or -1/2, but that’s it; we can’t fit any other values in between that are separated by at least one. For a spin-1 particle, we could measure the spin to be +1, -1, or 0. If we measure 0, that doesn’t mean the particle isn’t spinning; it just means its axis is perpendicular to the one along which we are measuring. No measurement will ever return an answer of 7/13 or the square root of two or anything crazy like that—quantum mechanics doesn’t allow it.

Degrees of freedom

At this point we need to draw a distinction between massive particles and massless ones. (See how this is going to connect back to the Higgs field?) It turns out that when you measure the spin of a massless particle, there are only two answers you can possibly get: plus the intrinsic spin or minus the intrinsic spin. (For spin-0 particles those are the same, and there’s only one possible answer.) In other words, no matter what axis you choose, when you measure the spin of a massless spin-1 particle like the photon along that axis, you will get either +1 or -1, never 0. For particles with spin-0 or spin-1/2, that doesn’t matter; there aren’t any missing values. But for higher-spin particles, it matters a lot. When we measure the spin of a photon or graviton, there are only two possible values we can get, but when we measure the spin of a W or Z boson, there are three different values, since it’s possible to get 0. In the figure, filled circles represent the results we can get when measuring the spin of a massless particle, while a massive particle could give us any of the filled or open circles.