The Sleepwalkers (10 page)
Authors: Arthur Koestler

However,
the
concept
armonia
did
not
have
quite
the
same
meaning
that
we
lend
to
"harmony".
It
is
not
the
pleasing
effect
of
simultaneously-sounded
concordant
strings
–
"harmony"
in
that
sense
was
absent
from
classical
Greek
music
–
but
something
more
austere:
armonia
is
simply
the
attunement
of
the
strings
to
the
intervals
in
the
scale,
and
the
pattern
of
the
scale
itself.
It
means
that
balance
and
order,
not
sweet
pleasure,
are
the
law
of
the
world.
Sweetness
does
not
enter
the
Pythagorean
universe.
But
it
contains
one
of
the
most
powerful
tonics
ever
administered
to
the
human
brain.
It
lies
in
the
Pythagorean
tenets
that
"philosophy
is
the
highest
music",
and
that
the
highest
form
of
philosophy
is
concerned
with
numbers:
for
ultimately
"all
things
are
numbers".
The
meaning
of
this
oft-quoted
saying
may
perhaps
be
paraphrased
thus:
"all
things
have
form,
all
things
are
form;
and
all
forms
can
be
defined
by
numbers".
Thus
the
form
of
the
square
corresponds
to
a
"square
number",
i.e.
16=4×4,
whereas
12
is
an
oblong
number,
and
6
a
triangular
number:

Numbers
were
regarded
by
the
Pythagoreans
as
patterns
of
dots
which
form
characteristic
figures,
as
on
the
sides
of
a
dice;
and
though
we
use
arabic
symbols,
which
have
no
resemblance
to
these
dot-patterns,
we
still
call
numbers
"figures",
i.e.
shapes.
Between
these
number-shapes
unexpected
and
marvellous
relations
were
found
to
exist.
For
instance,
the
series
of
"square
numbers"
was
formed
simply
by
the
addition
of
successive
odd
numbers:
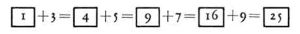
and
so forth:
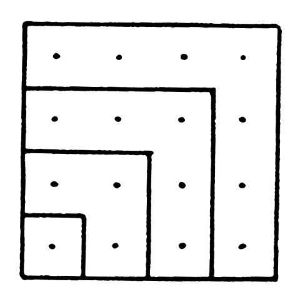
The
addition
of
even
numbers
formed
"oblong
numbers",
where
the
ratio
of
the
sides
represented
exactly
the
concordant
intervals
of
the
musical
octave:
2
(2
:
1,
octave)
+
4
=
6
(3
:
2,
fifth)
+
6
=
12
(4
:
3,
quart)
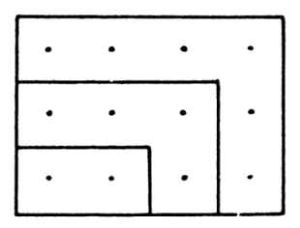
In
a
similar
manner,
"cubic"
numbers
and
"pyramidal"
numbers
were
obtained.
Mnesarchos
had
been
a
gem
engraver,
so
Pythagoras
in
his
youth
must
have
been
familiar
with
crystals
whose
form
imitated
those
of
pure
number-shapes:
quartz
the
pyramid
and
double-pyramid,
beryl
the
hexagon,
garnet
the
dodocaeder.
It
all
went
to
show
that
Reality
could
be
reduced
to
number-series
and
number-ratios,
if
only
the
rules
of
the
game
were
known.
To
discover
these
was
the
chief
task
of
the
Philosophos
,
the
Lover
of
Wisdom.
An
example
of
the
magic
of
numbers
is
the
famous
theorem,
by
which
alone
Pythagoras
is
consciously
remembered
today
–
the
visible
peak
of
the
submerged
iceberg.
*
There
is
no
obvious
relationship
between
the
lengths
of
the
sides
of
a
right-angled
triangle;
but
if
we
build
a
square
over
each
side,
the
areas
of
the
two
smaller
squares
will
exactly
equal
the
area
of
the
larger.
If
such
wonderfully
ordered
laws,
hitherto
hidden
from
the
human
eye,
could
be
discovered
by
the
contemplation
of
number-shapes,
was
it
not
legitimate
to
hope
that
soon
all
secrets
of
the
universe
would
be
revealed
through
them?
Numbers
were
not
thrown
into
the
world
at
random;
they
arranged
themselves
into
balanced
patterns,
like
the
shapes
of
crystals
and
the
concordant
intervals
of
the
scale,
according
to
the
universal
laws
of
harmony.