Thinking, Fast and Slow (51 page)
Read Thinking, Fast and Slow Online
Authors: Daniel Kahneman

Subjective probability distributions for a given quantity (the Dow Jones average) can be obtained in two different ways: (i) by asking the subject to select values of the Dow Jones that correspond to specified percentiles of his probability distribution and (ii) by asking the subject to assess the probabilities that the true value of the Dow Jones will exceed some specified values. The two procedures are formally equivalent and should yield identical distributions. However, they suggest different modes of adjustment from different anchors. In procedure (i), the natural starting point is one’s best estimate of the quantity. In procedure (ii), on the other hand, the subject may be anchored on the value stated in the question. Alternatively, he may be anchored on even odds, or a 50–50 chance, which is a natural starting point in the estimation of likelihood. In either case, procedure (ii) should yield less extreme odds than procedure (i).
To contrast the two procedures, a set of 24 quantities (such as the air distance from New Delhi to Peking) was presented to a group of subjects who assessed either
X
10
or
X
90
for each problem. Another group of subjects received the median judgment of the first group for each of the 24 quantities. They were asked to assess the odds that each of the given values exceeded the true value of the relevant quantity. In the absence of any bias, the second group should retrieve the odds specified to the first group, that is, 9:1. However, if even odds or the stated value serve as anchors, the odds of the second group should be less extreme, that is, closer to 1:1. Indeed, the median odds stated by this group, across all problems, were 3:1. When the judgments of the two groups were tested for external calibration, it was found that subjects in the first group were too extreme, in accord with earlier studies. The events that they defined as having a probability of .10 actually obtained in 24% of the cases. In contrast, subjects in the second group were too conservati
ve. Events to which they assigned an average probability of .34 actually obtained in 26% of the cases. These results illustrate the manner in which the degree of calibration depends on the procedure of elicitation.
Discussion
This article has been concerned with cognitive biases that stem from the reliance on judgmental heuristics. These biases are not attributable to motivational effects such as wishful thinking or the distortion of judgments by payoffs and penalties. Indeed, several of the severe errors of judgment reported earlier occurred despite the fact that subjects were encouraged to be accurate and were rewarded for the correct answers.
22
The reliance on heuristics and the prevalence of biases are not restricted to laymen. Experienced researchers are also prone to the same biases—when they think intuitively. For example, the tendency to predict the outcome that best represents the data, with insufficient regard for prior probability, has been observed in the intuitive judgments of individuals who have had extensive training in statistics.
[ti
cor pri
23
Although the statistically sophisticated avoid elementary errors, such as the gambler’s fallacy, their intuitive judgments are liable to similar fallacies in more intricate and less transparent problems.
It is not surprising that useful heuristics such as representativeness and availability are retained, even though they occasionally lead to errors in prediction or estimation. What is perhaps surprising is the failure of people to infer from lifelong experience such fundamental statistical rules as regression toward the mean, or the effect of sample size on sampling variability. Although everyone is exposed, in the normal course of life, to numerous examples from which these rules could have been induced, very few people discover the principles of sampling and regression on their own. Statistical principles are not learned from everyday experience because the relevant instances are not coded appropriately. For example, people do not discover that successive lines in a text differ more in average word length than do successive pages, because they simply do not attend to the average word length of individual lines or pages. Thus, people do not learn the relation between sample size and sampling variability, although the data for such learning are abundant.
The lack of an appropriate code also explains why people usually do not detect the biases in their judgments of probability. A person could conceivably learn whether his judgments are externally calibrated by keeping a tally of the proportion of events that actually occur among those to which he assigns the same probability. However, it is not natural to group events by their judged probability. In the absence of such grouping it is impossible for an individual to discover, for example, that only 50% of the predictions to which he has assigned a probability of .9 or higher actually came true.
The empirical analysis of cognitive biases has implications for the theoretical and applied role of judged probabilities. Modern decision theory
24
regards subjective probability as the quantified opinion of an idealized person. Specifically, the subjective probability of a given event is defined by the set of bets about this event that such a person is willing to accept. An internally consistent, or coherent, subjective probability measure can be derived for an individual if his choices among bets satisfy certain principles, that is, the axioms of the theory. The derived probability is subjective in the sense that different individuals are allowed to have different probabilities for the same event. The major contribution of this approach is that it provides a rigorous subjective interpretation of probability that is applicable to unique events and is embedded in a general theory of rational decision.
It should perhaps
be noted that, while subjective probabilities can sometimes be inferred from preferences among bets, they are normally not formed in this fashion. A person bets on team A rather than on team B because he believes that team A is more likely to win; he does not infer this belief from his betting prefere
nces. Thus, in reality, subjective probabilities determine preferences among bets and are not derived from them, as in the axiomatic theory of rational decision.
25
The inherently subjective nature of probability has led many st
udents to the belief that coherence, or internal consistency, is the only valid criterion by which judged probabilities should be evaluated. From the standpoint of the formal theory of subjective probability, any set of internally consistent probability judgments is as good as any other. This criterion is not entirely satisf
actory [ saf sub, because an internally consistent set of subjective probabilities can be incompatible with other beliefs held by the individual. Consider a person who
se subjective probabilities for all possible outcomes of a coin-tossing game reflect the gambler’s fallacy. That is, his estimate of the probability of tails on a particular toss increases with the number of consecutive heads that preceded that toss. The judgments of such a person could be internally consistent and therefore acceptable as adequa
te subjective probabilities according to the criterion of the formal theory. These probabilities, however, are incompatible with the generally held belief that a coin has no memory and is therefore incapable of generating
sequential dependencies. For judged probabilities to be considered adequate, or rational, internal consistency is not enough. The judgments must be compatible with the entire web of beliefs held by the individual. Unfortunately, there can be no simple formal procedure for assessing the compatibility of a
set of probability judgments with the judge’s total system of beliefs. The rational judge will nevertheless strive for compatibility, even though internal consistency is more easily achieved and assessed. In particular, he w
ill attempt to make his probability judgments compatible with his knowledge about the subject matter, the laws of probability, and his own judgmental heuristics and bia
ses.
Summary
This article described three heuristics that are employed in making judgments under uncertainty: (i) representativeness, which is usually employed when p
eople are asked to judge the probability that an object or event A belongs to class or process B; (ii) availability of instances or scenarios, which is often employed when people are asked to assess the frequency of a class or the plausibility of a particular development; and (iii) adjustment from an anchor, which is usually employe
d in numerical prediction when a relevant value is available. These heuristics are highly economical and usually effective, but they lead to systematic and predictable
errors. A better understanding of these heuristics and of the biases to which they lead could improve judgments and decisions in situations of uncertainty.
1.
D. Kahneman and A. Tversky, “On the Psychology of Prediction,”
Psychological Review
80 (1973): 237–51.
2.
Ibid.
3.
Ibid.
4.
D. Kahneman and A. Tversky, “Subjective Probability: A Judgment of Representativeness,”
Cognitive Psychology
3 (1972): 430–54.
5.
Ibid.
6.
W. Edwards, “Conservatism in Human Information Processing,” in
Formal Representation of Human Judgment
, ed. B. Kleinmuntz (New York: Wiley, 1968), 17–52.
="orm
7.
Kahneman and Tversky, “Subjective Probability.”
8.
A. Tversky
and D. Kahneman, “Belief in the Law of Small Numbers,”
Psychological Bulletin
76 (1971): 105–10.
9.
Kahneman and Tversky, “On the Psychology of Prediction.”
10.
Ibid.
11.
Ibid.
12.
Ibid.
13.
A. Tversky and D. Kahneman, “Availability: A Heuristic for Judging Frequency and Probability,”
Cognitive Psycholog
y
5 (1973): 207–32.
14.
Ibid.
15.
R. C. Galbraith and B. J. Underwood, “Perceived Frequency of Concrete and Abstract Words,”
Memory & Cognition
1 (1973): 56–60.
16.
Tversky and Kahneman, “Availability.”
17.
L. J. Chapman and J. P. Chapman, “Genesis of Popular but Erroneous Psychodiagnostic Observations,”
Journal of Abnormal Psychology
73 (1967): 193–204; L. J. Chapman and J. P. Chapman, “Illusory Correlation as an Obstacle to the Use of Valid Psychodiagnostic Signs,”
Journal of Abnormal Psychology
74 (1969): 271–80.
18.
P. Slovic and S. Lichtenstein, “Comparison of Bayesian and Regression Approaches to the Study of Information Processing in Judgment,”
Organizational Behavior & Human Performance
6 (1971): 649–744.
19.
M. Bar-Hillel, “On the Subjective Probability of Compound Events,”
Organizational Behavior & Human Performance
9 (1973): 396–406.
20.
J. Cohen, E. I. Chesnick, and D. Haran, “A Confirmation of the Inertial-? Effect in Sequential Choice and Decision,”
British Journal of Psychology
63 (1972): 41–46.
21.
M. Alpe [spa
Acta Psychologica
35 (1971): 478–94; R. L. Winkler, “The Assessment of Prior Distributions in Bayesian Analysis,”
Journal of the American Statistical Association
62 (1967): 776–800.
22.
Kahneman and Tversky, “Subjective Probability”; Tversky and Kahneman, “Availability.”
23.
Kahneman and Tversky, “On the Psychology of Prediction”; Tversky and Kahneman, “Belief in the Law of Small Numbers.”
24.
L. J. Savage,
The Foundations of Statistics
(New York: Wiley, 1954).
25.
Ibid.; B. de Finetti, “Probability: Interpretations,” in
International Encyclopedia of the Social Sciences
, ed. D. E. Sills, vol. 12 (New York: Macmillan, 1968), 496–505.
ABSTRACT: We discuss the cognitive and the psychophysical determinants of choice in risky and riskless contexts. The psychophysics of value induce risk aversion in the domain of gains and risk seeking in the domain of losses. The psychophysics of chance induce overweighting of sure things and of improbable events, relative to events of moderate probability. Decision problems can be described or framed in multiple ways that give rise to different preferences, contrary to the invariance criterion of rational choice. The process of mental accounting, in which people organize the outcomes of transactions, explains some anomalies of consumer behavior. In particular, the acceptability of an option can depend on whether a negative outcome is evaluated as a cost or as an uncompensated loss. The relation between decision values and experience values is discussed
.
Making decisions is like speaking prose—people do it all the time, knowingly or unknowingly. It is hardly surprising, then, that the topic of decision making is shared by many disciplines, from mathematics and statistics, through economics and political science, to sociology and psychology. The study of decisions addresses both normative and descriptive questions. The normative analysis is concerned with the nature of rationality and the logic of decision making. The descriptive analysis, in contrast, is concerned with people’s beliefs and preferences as they are, not as they should be. The tension between normative and descriptive considerations characterizes much of the study of judgment and choice.
Analyses of decision making commonly distinguish risky and riskless choices. The paradigmatic example of decision un ^v>
Risky Choice
Risky choices, such as whether or not to take an umbrella and whether or not to go to war, are made without advance knowledge of their consequences. Because the consequences of such actions depend on uncertain events such as the weather or the opponent’s resolve, the choice of an act may be construed as the acceptance of a gamble that can yield various outcomes with different probabilities. It is therefore natural that the study of decision making under risk has focused on choices between simple gambles with monetary outcomes and specified probabilities, in the hope that these simple problems will reveal basic attitudes toward risk and value.
We shall sketch an approach to risky choice that derives many of its hypotheses from a psychophysical analysis of responses to money and to probability. The psychophysical approach to decision making can be traced to a remarkable essay that Daniel Bernoulli published in 1738 (Bernoulli 1954) in which he attempted to explain why people are generally averse to risk and why risk aversion decreases with increasing wealth. To illustrate risk aversion and Bernoulli’s analysis, consider the choice between a prospect that offers an 85% chance to win $1,000 (with a 15% chance to win nothing) and the alternative of receiving $800 for sure. A large majority of people prefer the sure thing over the gamble, although the gamble has higher (mathematical) expectation. The expectation of a monetary gamble is a weighted average, where each possible outcome is weighted by its probability of occurrence. The expectation of the gamble in this example is .85 × $1,000 + .15 × $0 = $850, which exceeds the expectation of $800 associated with the sure thing. The preference for the sure gain is an instance of risk aversion. In general, a preference for a sure outcome over a gamble that has higher or equal expectation is called risk averse, and the rejection of a sure thing in favor of a gamble of lower or equal expectation is called risk seeking.
Bernoulli suggested that people do not evaluate prospects by the expectation of their monetary outcomes, but rather by the expectation of the subjective value of these outcomes. The subjective value of a gamble is again a weighted average, but now it is the subjective value of each outcome that is weighted by its probability. To explain risk aversion within this framework, Bernoulli proposed that subjective value, or utility, is a concave function of money. In such a function, the difference between the utilities of $200 and $100, for example, is greater than the utility difference between $1,200 and $1,100. It follows from concavity that the subjective value attached to a gain of $800 is more than 80% of the value of a gain of $1,000. Consequently, the concavity of the utility function entails a risk averse preference for a sure gain of $800 over an 80% chance to win $1,000, although the two prospects have the same monetary expectation.
It is customary in decision analysis to describe the outcomes of decisions in terms of total wealth. For example, an offer to bet $20 on the toss of a fair coin is represented as a choice between an individual’s current wealth
W
and an even chance to move to
W
+ $20 or to
W
n indispan> – $20. This representation appears psychologically unrealistic: People do not normally think of relatively small outcomes in terms of states of wealth but rather in terms of gains, losses, and neutral outcomes (such as the maintenance of the status quo). If the effective carriers of subjective value are changes of wealth rather than ultimate states of wealth, as we propose, the psychophysical analysis of outcomes should be applied to gains and losses rather than to total assets. This assumption plays a central role in a treatment of risky choice that we called prospect theory (Kahneman and Tversky 1979). Introspection as well as psychophysical measurements suggest that subjective value is a concave function of the size of a gain. The same generalization applies to losses as well. The difference in subjective value between a loss of $200 and a loss of $100 appears greater than the difference in subjective value between a loss of $1,200 and a loss of $1,100. When the value functions for gains and for losses are pieced together, we obtain an S-shaped function of the type displayed in Figure 1.
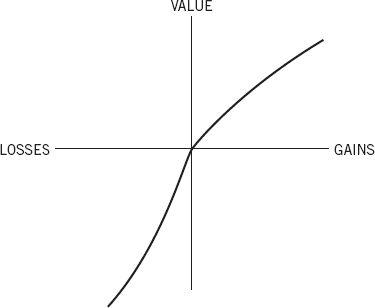
Figure 1. A Hypothetical Value Function
The value function shown in Figure 1 is (a) defined on gains and losses rather than on total wealth, (b) concave in the domain of gains and convex in the domain of losses, and (c) considerably steeper for losses than for gains. The last property, which we label
loss aversion
, expresses the intuition that a loss of $X is more aversive than a gain of $X is attractive. Loss aversion explains people’s reluctance to bet on a fair coin for equal stakes: The attractiveness of the possible gain is not nearly sufficient to compensate for the aversiveness of the possible loss. For example, most respondents in a sample of undergraduates refused to stake $10 on the toss of a coin if they stood to win less than $30.
The assumption of risk aversion has played a central role in economic theory. However, just as the concavity of the value of gains entails risk aversion, the convexity of the value of losses entails risk seeking. Indeed, risk seeking in losses is a robust effect, particularly when the probabilities of loss are substantial. Consider, for example, a situation in which an individual is forced to choose between an 85% chance to lose $1,000 (with a 15% chance to lose nothing) and a sure loss of $800. A large majority of people express a preference for the gamble over the sure loss. This is a risk seeking choice because the expectation of the gamble (–$850) is inferior to the expectation of the sure loss (–$800). Risk seeking in the domain of losses has been confirmed by several investigators (Fishburn and Kochenberger 1979; Hershey and Schoemaker 1980; Payne, Laughhunn, and Crum 1980; Slovic, Fischhoff, and Lichtenstein 1982). It has also been observed with nonmonetary outcomes, such as hours of pain (Eraker and Sox 1981) and loss of human lives (Fischhoff 1983; Tversky 1977; Tversky and Kahneman 1981). Is it wrong to be risk averse in the domain of gains and risk seeking in the domain of losses? These preferences conform to compelling intuitions about the subjective value of gains and losses, and the presumption is that people should be entitled to their own values. However, we shall see that an S-shaped value function has implications that are normatively unacceptable.
To address the normative issue we turn from psychology to decision theory. Modern decision theory can be said to begin with the pioneering work of von Neumann and Morgenstern (1947), who laid down several qualitative principles, or axioms, that should g ctha211;$850)overn the preferences of a rational decision maker. Their axioms included transitivity (if A is preferred to B and B is preferred to C, then A is preferred to C), and substitution (if A is preferred to B, then an even chance to get A or C is preferred to an even chance to get B or C), along with other conditions of a more technical nature. The normative and the descriptive status of the axioms of rational choice have been the subject of extensive discussions. In particular, there is convincing evidence that people do not always obey the substitution axiom, and considerable disagreement exists about the normative merit of this axiom (e.g., Allais and Hagen 1979). However, all analyses of rational choice incorporate two principles: dominance and invariance. Dominance demands that if prospect A is at least as good as prospect B in every respect and better than B in at least one respect, then A should be preferred to B. Invariance requires that the preference order between prospects should not depend on the manner in which they are described. In particular, two versions of a choice problem that are recognized to be equivalent when shown together should elicit the same preference even when shown separately. We now show that the requirement of invariance, however elementary and innocuous it may seem, cannot generally be satisfied.
Framing of Outcomes
Risky prospects are characterized by their possible outcomes and by the probabilities of these outcomes. The same option, however, can be framed or described in different ways (Tversky and Kahneman 1981). For example, the possible outcomes of a gamble can be framed either as gains and losses relative to the status quo or as asset positions that incorporate initial wealth. Invariance requires that such changes in the description of outcomes should not alter the preference order. The following pair of problems illustrates a violation of this requirement. The total number of respondents in each problem is denoted by
N
, and the percentage who chose each option is indicated in parentheses.
Problem 1 (
N =
152): Imagine that the U.S. is preparing for the outbreak of an unusual Asian disease, which is expected to kill 600 people. Two alternative programs to combat the disease have been proposed. Assume that the exact scientific estimates of the consequences of the programs are as follows:
If Program A is adopted, 200 people will be saved. (72%)
If Program B is adopted, there is a one-third probability that 600 people will be saved and a two-thirds probability that no people will be saved. (28%)
Which of the two programs would you favor?
The formulation of Problem 1 implicitly adopts as a reference point a state of affairs in which the disease is allowed to take its toll of 600 lives. The outcomes of the programs include the reference state and two possible gains, measured by the number of lives saved. As expected, preferences are risk averse: A clear majority of respondents prefer saving 200 lives for sure over a gamble that offers a one-third chance of saving 600 lives. Now consider another problem in which the same cover story is followed by a different description of the prospects associated with the two programs:
Problem 2 (
N
= 155):
If Program C is adopted, 400 people will die. (22%)
If Program D is adopted, there is a one-third probability that nobody will die and a two-thirds probability that 600 people will die. (78%)
It is easy to verify that options C and D in Problem 2 are undistinguishable in real terms from options A and B in Problem 1, respectively. The second version, however, assumes a reference state in which no one dies of the disease. The best outcome is the maintenance of this state and the alternatives are losses measured by the number of people that will die of the disease. People who evaluate options in these terms are expected to show a risk seeking preference for the gamble (option D) over the sure loss of 400 lives. Indeed, there is more risk seeking in the second version of the problem than there is risk aversion in the first.
The failure of invariance is both pervasive and robust. It is as common among sophisticated respondents as among naive ones, and it is not eliminated even when the same respondents answer both questions within a few minutes. Respondents confronted with their conflicting answers are typically puzzled. Even after rereading the problems, they still wish to be risk averse in the “lives saved” version; they wish to be risk seeking in the “lives lost” version; and they also wish to obey invariance and give consistent answers in the two versions. In their stubborn appeal, framing effects resemble perceptual illusions more than computational errors.