Understanding Sabermetrics (9 page)
Read Understanding Sabermetrics Online
Authors: Gabriel B. Costa,Michael R. Huber,John T. Saccoma

Figure 5.1 Computing the equivalence coefficient for batting
We see that the equivalence coefficient has enabled us to compile the entries in the following table, perhaps shedding some light to answer the questions we posed above:
•
What would Williams’ totals be if he had not lost so much time?
•
What if Ruth had not started out as a pitcher?
•
Who was the greater hitter: Williams or Ruth?
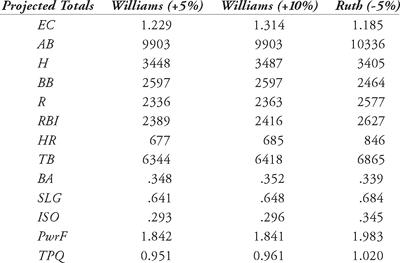
Table 5.2 Williams versus Ruth using the equivalence coefficient
So, who
was
the greater hitter?
was
the greater hitter?
Some remarks are in order regarding this approach. First, the EC can be regarded as a mathematical model. As with most models, it can be tweaked. For example, we assumed that Ted Williams was “equally better” during the years he missed in both the 1940s and in the 1950s. We could have assumed that he was 10 percent better in the 1940s and 5 percent better in the 1950s. Clearly, this would have yielded different projections and made our model a bit more complicated (see the
Hard Slider
problem at the end of the chapter).
Hard Slider
problem at the end of the chapter).
We also assumed that the proportions of AB to PA were constant
.
But if Williams was 10 percent better in the 1940s, perhaps he would have been even more selective regarding what pitches to hit, meaning that he might have had less than a total of 9903 AB, while drawing more than 2597 BB. How would this have affected his projected cumulative totals?
.
But if Williams was 10 percent better in the 1940s, perhaps he would have been even more selective regarding what pitches to hit, meaning that he might have had less than a total of 9903 AB, while drawing more than 2597 BB. How would this have affected his projected cumulative totals?
Also, this model could be enhanced by considering such entities as the hit-by-pitch (HBP) statistic, on-base-average (OBA) and both stolen bases (SB) and caught stealing (CS). In this way, more offensive categories would be included.
What about pitching? We mentioned legendary Dodger southpaw Sandy Koufax. Koufax recorded 2396 strikeouts (K) in 2324.3 innings pitched (IP) during his shortened career. What if, for the sake of argument, we assume that he had pitched
an additional 800
innings? Can we use the EC approach with respect to pitching? Yes, we can.
an additional 800
innings? Can we use the EC approach with respect to pitching? Yes, we can.
To find Koufax’s strikeout EC, we basically duplicate the procedure we used with the projected career cumulative hitting records of Ruth and Williams, since strikeouts are also a cumulative statistic. That is, we replace AB by K and substitute IP for PA. So if
x
is the number of additional K, and we assume an extra 800 IP, then
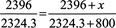 yielding
yielding
x
= 825 additional K, when we solve for
x.
So the predicted prorated career strikeout total for Koufax would be 2396 + 825 = 3221.
x
is the number of additional K, and we assume an extra 800 IP, then
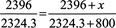
x
= 825 additional K, when we solve for
x.
So the predicted prorated career strikeout total for Koufax would be 2396 + 825 = 3221.
Now, let us further assume that Koufax would have been a 6 percent better pitcher during these additional 800 innings. Our kicker,
k
, is therefore 1.06. Hence, our new additional strikeout total becomes (1.06)825 = 875, giving a projected career total of 2396 + 875 = 3271 We note that we could have arrived at this figure by using the formula
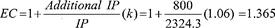 and computing (1.365)(2396) = 3271.
and computing (1.365)(2396) = 3271.
k
, is therefore 1.06. Hence, our new additional strikeout total becomes (1.06)825 = 875, giving a projected career total of 2396 + 875 = 3271 We note that we could have arrived at this figure by using the formula
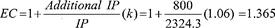
We summarize the technique of computing the EC for K in Figure 5.2.

Figure 5.2 Computing the equivalence coefficient for strikeouts
This technique can be used for all cumulative pitching statistics such as shutouts, decisions, etc. However, the approach must be modified when considering such statistics as earned run average.
A former sabermetrics student at Seton Hall University, Patrick Forgione, derived the following EC approach for projecting pitchers’ ERA:
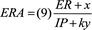 where ER are the number of earned runs allowed and
where ER are the number of earned runs allowed and
x
is the additional number of ER allowed; IP is the number of innings pitched and
y
is the additional number of IP;
k
is the kicker, where, as before,
k
> 1, if the pitcher is “better” and
k
< 1, if the pitcher is “worse.”
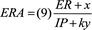
x
is the additional number of ER allowed; IP is the number of innings pitched and
y
is the additional number of IP;
k
is the kicker, where, as before,
k
> 1, if the pitcher is “better” and
k
< 1, if the pitcher is “worse.”
To illustrate this, we consider the case of Dizzy Dean referenced at the beginning of this chapter. We first must determine reasonable values of
x
and
y
which should be based on his record. One way to approach this is to make certain assumptions, much like we did in the Ruth-Williams discussion above. Let’s give Dean an additional 1000 IP; since Dean yielded 661 ER in 1963.66 IP, he averaged 0.337 ER / IP. If we simply prorate these numbers, then Dean would have given up a total of 337 ER in the additional 1000 IP (just multiply .337 by 1000). This preserves his lifetime ERA of 3.02.
x
and
y
which should be based on his record. One way to approach this is to make certain assumptions, much like we did in the Ruth-Williams discussion above. Let’s give Dean an additional 1000 IP; since Dean yielded 661 ER in 1963.66 IP, he averaged 0.337 ER / IP. If we simply prorate these numbers, then Dean would have given up a total of 337 ER in the additional 1000 IP (just multiply .337 by 1000). This preserves his lifetime ERA of 3.02.
But what if we assume that he would have been 5 percent better during these additional innings? This means that the “kicker”
k
has a value of 1.05. We now multiply the 1000 IP by 1.05. Using the formula above to project Dean’s ERA, we have
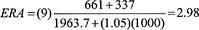 as his projected ERA.
as his projected ERA.
k
has a value of 1.05. We now multiply the 1000 IP by 1.05. Using the formula above to project Dean’s ERA, we have
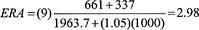
As in the case of hitting, this instrument can be tweaked in many ways, and, as is in the case of all modeling, care must be exercised regarding any sort of prediction or projection.
A subtle mathematical observation should be made here regarding the EC approach pertaining to statistics like ERA. Because ERA is an average, rather than a cumulative statistic, and because there are two terms in both the numerator and the denominator, the coefficient for this statistic is nothing more than the kicker, which appears in the denominator of the formula.
We summarize the technique of using the EC approach for ERA in Table 5.3 on page 38.

Table 5.3 Computing the equivalence coefficient for earned run average
We end this chapter with a few words about what has been called the “unmeasurable” aspect of baseball: fielding. By its very nature, fielding is more subjective than hitting and pitching. (For instance, when is a catch “great”?) And, as was mentioned above, there are relatively few fielding measures discussed in baseball. Traditionally, assists (A), putouts (PO) and errors (E) have been the three most important components in virtually all fielding metrics — with Passed Balls (PB) included for catchers.
This being said, for cumulative statistics, such as career A or PO, the EC may be used, in virtually the same way we applied it in our discussions above pertaining to Ruth, Williams and Koufax.
For relative measures such as Fielding Average (FA) which is given by
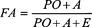 and Range Factor (RF) which is defined as
and Range Factor (RF) which is defined as
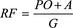 where
where
G
is the number of games played, the use of the EC concept would be applied in a similar way to that of Dizzy Dean ERA projection above. We will revisit the concept of the EC in subsequent chapters (for example, see Inning 9: Creating Measures and Doing Sabermetrics — Some Examples).
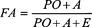
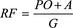
G
is the number of games played, the use of the EC concept would be applied in a similar way to that of Dizzy Dean ERA projection above. We will revisit the concept of the EC in subsequent chapters (for example, see Inning 9: Creating Measures and Doing Sabermetrics — Some Examples).
Other books
Dawn of Darkness (Daeva, #1) by Daniel A. Kaine
Ruined by a Rake by Erin Knightley
Carter by R.J. Lewis
Christmas Kisses (Romance on the Ranch Series #5) by Clay, Verna
Last Night by Meryl Sawyer
Rise by Karen Campbell
The Death of an Irish Lover by Bartholomew Gill
Whisper and Rise by Jamie Day
Obsessed: America's Food Addiction--And My Own by Mika Brzezinski