Warped Passages (56 page)

Another attractive feature of the lightest of the KK particles with nonzero extra-dimensional momentum is that its momentum (and hence its mass) is smaller when the extra dimension is bigger. A larger
observable consequences because lighter particles are easier to produce and discover.
If extra dimensions do exist, this lightest KK particle would not be the sole evidence for them. Other, higher-momentum particles would leave even sharper fingerprints of extra dimensions at particle colliders. These particles would have probability waves that oscillate more than once when traversing the curled-up dimension. Because the
n
th such particle would correspond to a wave that oscillated
n
times as it wound around the rolled-up dimension, the masses of these KK particles would all be integer multiples of the lightest one. And the higher the momenta, the sharper the fingerprints of extra dimensions that the KK particles will leave at particle colliders. Figure 74 schematically shows the values of KK particle masses, which are proportional to the inverse size of the extra dimension, and a couple of waves that correspond to these massive particles.
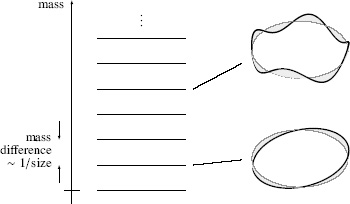
Figure 74.
Kaluza-Klein particles correspond to the waves that oscillate an integer number of times around the curled-up dimension. Waves with more oscillations correspond to heavier particles.
The many successively heavier KK particles resemble the multiple generations of an immigrant family. The members of the youngest generation who were born in the USA fully assimilate American culture, speak English perfectly, and don’t betray their foreign roots at all. That isn’t as true for the previous generation, the parents of this youngest generation: perhaps they speak with a trace of an accent,
and occasionally tell a few proverbs from the old country. The generation that is older still would sound even more foreign, and wear clothing and tell stories that originated in their homeland. These earlier generations might be said to add cultural dimensions to what would otherwise be a less colorful, uniform society.
Similarly, the lightest KK particles are indistinguishable from particles in a fundamentally four-dimensional world; only the more massive “older relations” would reveal evidence of extra dimensions. Although the lightest of the KK particles would appear to be four-dimensional, their provenance would become apparent once sufficient energy to produce the more massive “elders” was achieved.
If experimenters discover new heavy particles with the same charges as familiar ones and masses that are similar to one another, those particles will be strong evidence of extra dimensions. If such particles share the same charges and occur at regular intervals of mass, it would very likely mean that a simple curled-up dimension has been discovered.
But more complicated extra-dimensional geometries will yield more complicated patterns of masses. If enough such particles are discovered, the KK particles would then reveal not only the existence of extra dimensions, but also the extra dimensions’ sizes and shapes. No matter what the geometry of the hidden dimensions, the KK particles’ masses would depend on it. In all cases, the KK particles and their masses could tell us quite a lot about extra-dimensional properties.
Experimental Constraints
Until recently, most string theorists assumed that extra dimensions are no bigger than the minuscule Planck scale length. This is because gravity becomes strong at the Planck scale energy, and a theory of quantum gravity, which could be string theory, should take over at that point. But the Planck scale length is far smaller than any length we can study experimentally. The tiny Planck scale length corresponds (according to quantum mechanics and special relativity) to the enormous Planck scale mass (or energy)—ten thousand trillion times the
reach of current particle accelerators. Planck-mass KK particles would be so heavy that they would be well out of range of any conceivable experiment.
However, perhaps extra dimensions are bigger and KK particles are lighter. Why not ask instead what experimental tests tell us about an extra dimension’s size? What do we really know, theoretical prejudice aside?
If the world is higher-dimensional and there are no branes, then all familiar particles—the electron, for example—would have KK partners.
32
These would be particles that have exactly the same charge as familiar particles, but carry momenta in the additional dimensions. The electron’s KK partners would be negatively charged like the electron, but heavier. If an extra dimension is rolled up into a circle, the mass of the lightest such particle would differ from the electron’s mass by an amount inversely proportional to the extra dimension’s size. That means that, the larger the extra dimension, the smaller the particle’s mass. Because a bigger dimension would give rise to lighter KK particles, none of which have been seen in experiments, the bounds on KK particles’ masses constrain the allowed size of an extra curled-up dimension.
So far there has not been any sign of such charged particles at colliders operating at energies up to about 1,000 GeV. Since the KK particles would be signatures of extra dimensions, our not yet having seen them tells us that extra dimensions cannot be too large. Current experimental constraints tell us that extra dimensions cannot be any larger than 10
-17
cm (one hundred-thousandth of a trillionth of a centimeter).
*
This is extremely small—far smaller than anything we can see directly.
This limit on an extra dimension’s size is about ten times smaller than the weak scale length. But even though 10
-17
cm is small, it is huge compared with the Planck scale length, which is 10
-33
cm, sixteen orders of magnitude smaller. This means that extra dimensions could be much bigger than the Planck scale length and still have evaded detection. The (modern) Greek physicist Ignatius Antoniadis was one
of the first to imagine that extra dimensions were not the Planck length, but were instead comparable in size to the length scale associated with the weak force. He was thinking about what new physics might appear when colliders increase their energy even a little. After all, the hierarchy problem tells us that something must be seen at those energies, at which particles will be produced with weak scale energies and masses.
But even the above limit on the size of extra dimensions doesn’t necessarily always apply. KK particles are fingerprints of extra dimensions, but they can be wily and surprisingly hard to find. We’ve recently learned a lot more about KK particles and what they might look like. The following chapters will explain the latest results about why, once branes come into the picture, extra dimensions can be bigger than 10
-17
cm and still escape detection—even though you’d expect bigger dimensions to give rise to lighter KK particles. Some models with surprisingly large dimensions—dimensions that you might have thought would have very visible consequences—can be invisible yet nonetheless help to explain the mysterious properties of Standard Model particles. And Chapter 22 will present an even more surprising result: an infinitely large extra dimension could give rise to infinitely many light KK particles, yet nonetheless leave no observable trace.
What’s New
- Kaluza-Klein (KK) modes are particles that carry extra-dimensional momentum; they are higher-dimensional interlopers in our four-dimensional world.
- KK particles would look like heavy particles with the same charges as known particles.
- KK particles’ masses and interactions are determined by the higher-dimensional theory; they therefore reflect the properties of the higher-dimensional spacetime.
- If we could find and measure the properties of all KK particles, we would know the size and shape of the higher dimensions.
- Current experimental constraints tell us that if all particles travel through higher-dimensional space, extra dimensions can be no bigger than about 10
-17
cm.
Voluminous Passages: Large Extra Dimensions
I couldn’t even see the millimeter when it fell.
Eminem
Now that K. Square’s brief visit was over, Athena spent a lot of time at the local Internet cafe. She was exhilarated by her recent discovery of some mysterious new websites, the most intriguing of which was xxx.socloseandyetsofar.al. Athena suspected that these suggestive sites were a consequence of the recent AOB (America on Brane)/Spacetime Warner multimedia merger, but she had to go home before she had time to investigate.
When Athena arrived at her house she rushed to her computer, where she once again sought the exotic hyperlinks that had been so readily accessible at the Internet cafe. To her frustration, however, CyberNanny prevented her from reaching the forbidden dimensionally enhanced sites.
*
But by cloaking her identity with her secure alias, Mentor, Athena vanquished her cybercensor and succeeded in finally returning to the mysterious hyperlinks.
Athena secretly hoped that K. Square had sent her a message that was hidden in a webpage. But the sites were not easy to understand, and she managed to pick up only a few potentially meaningful signals. She resolved to study their content some more and hoped the merger—unlike the other merger with a similar name—would last long enough for her to figure them out.
At the Oxford supersymmetry conference in 1998, the Stanford physicist Savas Dimopoulos gave one of the most interesting talks. He reported on work he had done in collaboration with two other physicists, Nima Arkani-Hamed and Gia Dvali. The colorful names of these three match their colorful characters and ideas. Savas gets very excited about his projects; his collaborators tell me that his enthusiasm is always contagious. He was so taken with extra dimensions that he told a colleague that all the new unexplored physics ideas made him feel like a kid in a candy store—he wanted to eat it all before anyone else got any. Gia, a physicist from former Soviet Georgia, takes great risks, both in his approach to physics and in his audacious feats of mountaineering. He was once stuck without any food on a stormy mountaintop in the Caucusus for two nights. Nima, a physicist from an Iranian family, is very energetic, stimulating, and vividly articulate. Now my Harvard colleague, he often roams the hallways enthusiastically explaining his latest research and convincing others to join in.
Ironically, Savas’s talk at the supersymmetry conference, which was not about supersymmetry at all but was instead about extra dimensions, stole some of supersymmetry’s thunder. He explained that extra dimensions, rather than supersymmetry, could be the physical theory underlying the Standard Model. And if his suggestion was correct, experimenters could expect to find evidence of extra dimensions, rather than supersymmetry, when they explore the weak scale in the near future.
This chapter presents Arkani-Hamed, Dimopoulos, and Dvali’s
*
idea about how very large dimensions might explain the weakness of gravity. In essence, large extra dimensions could dilute the gravitational force so much that gravity’s strength would be much weaker than estimates without extra dimensions would have you believe. Their models don’t actually solve the hierarchy problem because you still have to explain why the dimensions are so large. But ADD hoped this new and different question would be more tractable.
We’ll also consider the related question ADD asked: how big can rolled-up extra dimensions be if Standard Model particles are confined
to a brane and are not free to travel in the bulk without contradicting experimental results? The answer they found was extraordinary. At the time they wrote their paper, it looked like extra dimensions could be as big as a millimeter.
Dimensions (Almost) as Large as a Millimeter
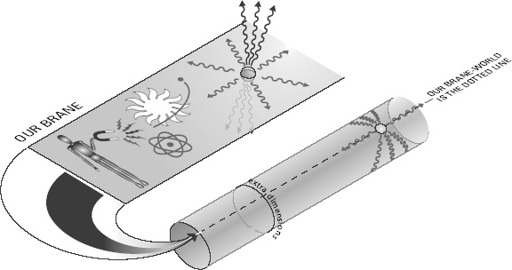
In the ADD model, as in the sequestering model I described in Chapter 17, the Standard Model particles are confined to a brane. However, the two models had very different objectives, so their remaining features are completely different. Whereas the sequestering model had one additional dimension that was bounded between two branes, the ADD models all have more than one dimension and those dimensions are curled up. Depending on the details of the implementation, space in their models contains two, three, or more additional curled-up dimensions. Moreoever, the ADD model contains a single brane on which the Standard Model particles are confined, but that brane does not bound space. It simply sits inside the extra curled-up dimensions, as is illustrated in Figure 75.
33