Where the Conflict Really Lies: Science, Religion, and Naturalism (28 page)

The suggestion is that perhaps
our
universe
couldn’t have had
different values for its parameters.
³⁴
Let a, b, c, and d be the values displayed by the strength of the four fundamental forces in our universe: the suggestion is that our universe has essentially the property of being such that the strength of those four forces is a,
b, c, and d. In every possible world in which this universe exists, it is such that those forces display these values. This very universe could perhaps have been different in many ways: there are possible worlds, perhaps, in which it contains more or fewer stars, or more or fewer horses; but none in which it displays different values for those parameters. But then the probability that
this
universe should be fine-tuned for life is 1, and is 1 on any hypothesis—chance, design, whatever you like.

Is it plausible or reasonable to claim that this universe has these properties essentially? An important question, obviously, is one Manson raises: what sort of thing
are
these universes? A prior question: are these universes
things
—that is, substances—at all? We talk as if there are such things as heaps or piles of sand; but it is also plausible to think there really aren’t any such things. There are (as we may suppose for purposes of argument) grains of sand; but it is not obvious that a multitude of grains of sand located close to each other combine to make up still another thing in addition to those grains of sand, namely a heap of them. In the same way, perhaps a universe is just an assemblage, a pile or heap of other things—stars and planets, or living things, or atoms, or elementary particles. So are there any such things as universes? Or is talk involving “universes” just a
façon de parler
, to be paraphrased into sentences that aren’t even ostensibly about universes, but about things of other sorts—elementary particles, for example?

It would be nice if we didn’t have to settle this difficult question in order to evaluate the multiverse objection. And perhaps we don’t. For suppose there really aren’t any such things as universes, but only (say) elementary particles and things composed of them—animals, for example. Then what would it mean to say that our universe has the property of being such that the strengths of those four forces are a, b, c, and d? Presumably that those elementary particles spatio-temporally related to us, and whatever is made of them, have the relevant properties. And to say that a universe has these properties
essentially
would just be to say that those elementary particles have these properties essentially. We can then restate the objection (to the “this universe” objection to the multiverse objection to the FTA): the elementary particles that are spatiotemporally related to those that are, say, parts of our body, have the above properties essentially. And then we can also restate our question: is it reasonable or plausible to hold that those elementary particles do have those properties essentially?

To begin with, we certainly don’t
see
any impossibility in these particles’ being such that the four forces display somewhat different strengths. There is certainly no contradiction there, and it does not seem that there is incoherence or impossibility in the broadly logical sense. Of course it is important, here, to distinguish carefully between
failing to see that there is an impossibility
and
seeing that there is no impossibility
. Our knowledge or grasp of such esoterica as quarks and gluons is pretty insubstantial; our failure to see that certain properties are essential to them is probably not of great significance. Our intuitions about elementary particles are faint and probably not worth a lot; they are too far from the areas where we have experience, too far from the areas where we can think to some purpose.

Still, we have stronger and more reliable intuitions about some of the things these particles compose—trees and animals, for example. And here it certainly seems that these things could exist even if the parameters in question had slightly different values. Aren’t there possible worlds that are just like the actual world except that the law of gravity isn’t inversely proportional to r
²
, but to r
^{20 …01}
? Isn’t it possible in the broadly logical sense that you and I (more exactly, our bodies) should have existed even if the law of gravity had been different in that minute way? It certainly seems so.
³⁵

So how do things stand with the “essential properties” objection to the “this universe objection” to the “multiverse objection to the fine-tuning argument” (whew!)? It’s clearly not a strong objection. The multiverse objection, recall, goes like this: it could be that there is no designer, but there are very many different universes, with the values of the parameters set at random or by chance; among them would be our universe, where the parameters are life-permitting. Given that there is this whole vast ensemble of universes, the probability that at least one of them is fine-tuned would be high; and (it is suggested) this is a good
counter to the FTA. The rejoinder: though it is indeed true that given many universes, the probability is high that at least one of them is fine-tuned, the same can’t be said for the probability that
our
universe is fine-tuned; that probability remains what it was on the atheistic single-universe hypothesis. The counter-rejoinder from the opponents of the FTA: perhaps our universe could not have had values for its free parameters different from the ones it does have: it has those values
essentially
, in which case the probability that it is fined-tuned on any hypothesis is very high, indeed, 1. And the proper response to that is that there is certainly no reason at all to think that if there are many universes, they will have essentially the property of displaying the values, for those parameters, that they do in fact display. There isn’t any reason at all to accept this essential properties objection.

Of course at this point the opponent of the FTA is not obliged to assert that our universe
is
essentially fine-tuned. It is enough if this is possible—that is, epistemically possible. It is enough if, for all we know, there are many different universes, and they have essentially the values for the four forces they do in fact display, or at any rate are such that those of them that are fine-tuned are essentially fine-tuned, or more weakly yet, that our universe is essentially fine-tuned. Is this epistemically possible? Is it true for all we know? Well, I doubt that we
know
that it is false. Of course to require that we know that it is false is to set the bar very high—with respect to arguments like this, we can seldom claim that we
know
that their premises are true (or for that matter false). It does seem that it is
epistemically unlikely
that our universe is essentially fine-tuned; after all, the whole discussion began with the fact that its being fine-tuned seems to be an enormous and fortuitous coincidence. And that means, I think, that the FTA survives this objection in reasonably good shape. The FTA is far from conclusive; it is epistemically probable, though by no means epistemically certain, that our universe could have failed to be fine-tuned; therefore the probability that it
is
fine-tuned, given the atheistic many-universe hypothesis, is low, much lower than on the hypothesis of theism. So far the FTA survives—bloody, perhaps, but unbowed.
³⁶

There is still another objection to the FTA, one requiring a little stage setting. There are fundamentally three ways the FTA can be stated, three forms it can take. First, it can be thought of as an inference to the best explanation. The best explanation of the fine-tuning of our universe is theism; alternatively, theism is a better explanation of fine-tuning than any atheistic explanation; and that means that, at least with respect to the phenomenon of fine-tuning, theism is to be preferred to atheism. (Of course there may be other phenomena such that atheism explains
them
better than theism.)

Second, the argument can be stated in terms of Bayes’ theorem, a theorem of the probability calculus, which tells us that the probability of a hypothesis H on evidence E is equal to the probability of H times the probability of E given H, divided by the probability of E. As specified to the case in hand:

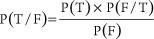
where T is theism and F is the proposition that our universe is fine-tuned. P(T) and P(F) are the
antecedent
probabilities of theism and fine-tuning. The antecedent probability of theism, we may say, is the probability of theism before the evidence of fine-tuning is taken into account; the antecedent probability of fine-tuning is its probability prior to our discovery that the universe is indeed fine-tuned for life.
³⁷
The idea would be to compare the probability of theism, given fine-tuning, with the probability of the atheistic hypothesis, given fine-
tuning; and the thought would be that the former is greater than the latter. This would suggest that with respect to the evidence of fine-tuning, theism is to be preferred to atheism. That’s the second way to take the FTA.

A third way: some philosophers, for example Elliott Sober, object to this way of stating the argument, claiming that those antecedent probabilities are too hard to discover—or perhaps too subjective, in that different people will make very different estimates of them. They therefore propose a “likelihood” version of the argument. In Bayes’ theorem, the second term in the numerator (in the above example, “P(F/T)”) is called the
likelihood
; in the likelihood version of the argument, we make no references to antecedent probabilities, but think only about the likelihoods. We compare the probability of fine-tuning given theism with the probability of fine-tuning given the atheistic hypothesis: P(F/T) vs. P(F/A). If the former is greater than the latter, then, again with respect to the evidence of fine-tuning, theism is to be preferred to atheism. We could put it like this: if fine-tuning is more to be expected given theism than given atheism, then the existence of fine-tuning confirms theism over atheism. The likelihood version of the FTA, therefore, claims that P(F/T) is greater than P(F/A), in which case theism is to be preferred to atheism, at least with respect to fine-tuning.

Now we can turn to the objection. Suppose we think about the likelihood version of the FTA: we are to compare P(F/T) with P(F/A). But can we make a sensible estimate of P(F/T)? Elliott Sober thinks not:

The problem is to say how probable it is, for example, that the vertebrate eye would have features F1,… Fn if the eye were produced by an intelligent designer….. The problem is that the design hypothesis confers a probability on the observation only when it is supplemented with further assumptions
about what the Designer’s goals and abilities would be if He existed.
³⁸

Sober is not thinking about the God of theism, here, but more broadly about a designer of some sort or other. Still, his problem can also be raised with respect to God. God is transcendent; his ways are not our ways; his purposes are inscrutable; can we really say how probable it is that God would create the vertebrate eye, or, more relevantly, would fine-tune the universe? Do we know enough about God to say what this probability is, even within very wide limits? Sober thinks not. If so, we can’t sensibly claim that P(F/T) is greater than P(F/A).

But why can’t we just add to theism those further assumptions Sober speaks of? Why not revise the theistic FTA by adding some further propositions to the hypothesis? For example, we could take the hypothesis to be, not just as

T There is such a person as God,

but as the proposition that

T* There is such a person as God and he wants there to be life;

P(F/T*) would certainly seem to be greater than P(F/A).

That looks good, except that two can play at this game. Why can’t the atheist, in response, beef up A to

A* There is no such person as God and the universe has a powerful intrinsic impulse towards the existence of life?

P(F/T*) isn’t obviously greater than P(F/A*). But the theist can then respond by replacing T* with

T** There is such a person as God, and he really, really wants there to be intelligent life of the sort requiring fine-tuning.

Of course the atheist can respond with an A** on which fine-tuning is even more probable. What we get here is a sort of arms race in which each side can produce a series of hypotheses on which F is ever more probable; indeed, each can finally produce a hypothesis on which the probability of F is 1. You might think that these hypotheses become more and more improbable; but on the likelihood version of the argument, we don’t take the prior probabilities of the hypotheses into account; hence in thinking about the likelihood version of the FTA, we can’t raise this as an objection to the arms race. On the likelihood version of the argument, how can we determine which hypotheses are to be compared, i.e., how can we determine which are the right ones with respect to which to estimate the probability of fine-tuning? On the Bayes theoretic version of the FTA, it is the prior probabilities that perform that function; but on the likelihoods version we have to ignore them.