125 Physics Projects for the Evil Genius (23 page)
Read 125 Physics Projects for the Evil Genius Online
Authors: Jerry Silver

If m1 is the larger mass, the acceleration is in the direction of the larger mass going down.
The force on the system is F = g(m1 − m2). According to Newton’s second law, this equals the total mass times the acceleration. Because the total mass is (m1 + m2), we can derive the previous expression for acceleration.
Once you get the idea of this, try it at an incline, as shown in
Figure 31-2
.
Predict what angle or combination of masses will result in equilibrium.
Because friction helps establish stability, a window is around the predicted conditions that will also result in equilibrium. This can also be done with each of the two masses sliding on an incline.
An Atwood machine demonstrates the principles of Newton’s second law. The net force on the masses causes the total mass of the system to accelerate.

Figure 31-2
Atwood’s machine on an incline
.
Terminal velocity. Falling slowly
.
Shortly after jumping from an airplane, skydivers reach a steady velocity instead of constantly accelerating as do other more streamlined objects subjected to Earth’s gravity. When this happens, the skydiver falls at a terminal velocity that is nearly constant. This is fortunate because, once the parachute opens, it is much easier to slow the skydiver’s fall. Had the skydiver been a rock in a vacuum without the benefit of air resistance, it would reach a much higher velocity.
- coffee filter
- meterstick
- stopwatch
- coin, book, or another compact object
- optional: motion sensor
- Drop a coffee filter from a measured distance.
- Compare the time it takes to fall with a coin or a book.
- Compare the distance versus the time graph generated by a motion sensor for each of the two objects.
Not only will the coffee filter take longer to descend, but more significantly, it falls at a steady velocity. The coin, typical of other objects in free-fall, accelerates as it falls and will have an ever-increasing velocity. The following shows distance versus time and velocity versus time graphs for these two objects. Notice the falling book continues to accelerate as it falls. This is indicated by the curved shape of the position-time graph and the positive slope for the velocity-time graph.
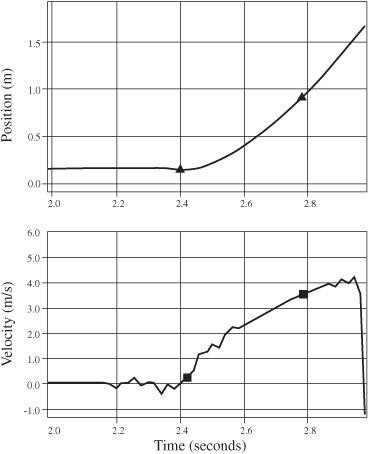
Figure 32-1
Falling book
.
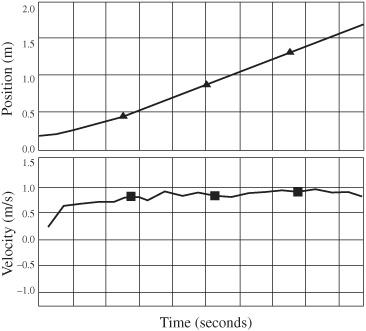
Figure 32-2
Falling coffee filter
.
The coffee filter falls with constant velocity. The position-time graph is a straight line and the velocity-time graph is essentially a horizontal line, indicating a constant velocity during the descent.
When a falling object encounters significant air resistance, the faster the object falls, the greater the force opposing its descent. So, the more gravity tries to pull the object down, the more determined the air resistance is to oppose gravity. As a result, equilibrium is established with the object falling at a constant terminal velocity.
Compare the descent of bottle rockets (described in
Project 27
) with and without parachutes.
Free-fall is different than an object subjected to drag forces.
An object in free-fall accelerates with a constant rate of 9.8 m/s
2
. An object subject to a drag force does not accelerate, but reaches a steady constant velocity, called the
terminal velocity
.
Balancing act. Painter on a scaffold
.
A scaffold is built from a board placed across a base without anything holding it down. How far from the edge of the board can a painter stand without tipping the board? This experiment investigates the condition for stability called
static equilibrium
.
- section of a 2″ × 4″ block about 6″ long
- meterstick
- 20 g mass
- Set the block on the table. This can be either with the 2” edge parallel to the table or the 2” edge perpendicular to the table. Each case gives a different result.
- Measure the mass of the meterstick.
- Lay the meterstick over the block, as shown in
Figure 33-1
, with the 50-centimeter mark of the meterstick centered over the middle of the block. - Predict how far the 20-gram mass (the “painter”) can be placed from the center without tipping the meterstick, as is the case shown in
Figure 33-2
. - The principle to use is that the torque trying to tip the “scaffold” must not be greater than the torque that holds it in place. Here are the formulas:
Tipping torque
1w
1
2w
2
d
1
= distance from edge of block to center of 20g mass
w
1
= weight of block
d
2
= distance from edge of block to the 50 cm mark of the meterstick
w
2
= weight of the meterstick
A 2″ × 4″ block has actual measurements of 1½″ × 3½″ (or 3.8 cm × 8.9 cm). (The 3.8 cm side is the height and the 8.9 cm side is the width of the block.) The distance, d
2
, is one-half the supporting edge. This would be 4.45 cm (with the width of the block along the table) or 1.6 cm (with the height of the block on the table).
6. Try it with other masses.
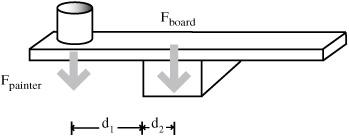
Figure 33-1
How far can the “painter” move toward the edge of the board
?

Figure 33-2
Here the “painter” has gone too far
.
For a 90-gram mass meterstick balanced on top of a nominally 2” × 4” block, the following table shows the maximum distance the painter, m2, can go without toppling the meterstick.

The amount of mass carried at a point of support is the result of a torque generated around the pivot point. In this case, the spring scales form a pivot point. The greater the mass supported, and the further from the pivot point, the greater the torque.
Place two bathroom scales on the floor separated by the length of the board. Set a stiff board about 8 feet long over each scale. Adjust the scales to read zero, to eliminate the effect of the weight of the board. Predict and measure the reading directly over the scales, in the middle, and at arbitrary positions in between.
