125 Physics Projects for the Evil Genius (22 page)

Figure 28-2
Newton’s third law: The bouyant force pushes up. The opposite reaction pushes the scale down
.

This is similar to the enigma: if birds are in a truck, will the truck weigh less if the birds are flying, instead of at rest on the floor of the truck bed? It turns out that the force exerted by the birds’ wings exerts the same downward pressure on the truck bed as the weight of the birds at rest. (As with the previous experiment, this is also addressed by a
Mythbusters
episode.)

This experiment shows how a reaction force is established by Newton’s third law.

This project compares the amount of friction developed by various common substances. It also shows a simple way to measure the amount of friction.

• book
  
• coin
  
• ice cube
  
• rubber eraser
  
• protractor
  

1. Line all three objects up in a straight line on the book.
   
2. Slowly lift the book.
   
3. As you raise the book, note the angle where each of the objects just begins to slide.
   
4. Break the rubber eraser into various pieces of different areas.
   
5. Line up the eraser pieces and determine the sequence in which they slide.
   
6. Break the ice cube into various sized pieces in different areas.
   
7. Line the eraser pieces up and determine the sequence in which they slide.
   

The ice goes first, then the coin, and then, finally, the eraser.

For a given material, the contact area between the sliding surfaces does not significantly affect the force of friction.

The surface of each material is characterized by a different amount of friction. It would be nice if this was called the surface’s “slipperiness.” However, it goes under the more prestigious name of
coefficient of friction
, which is the amount of frictional force a surface imposes on an object compared to its weight (on a horizontal surface). There is a frictional force to get something going (
static friction
) and a force to keep something going (
kinetic friction
). The frictional force depends on the coefficient of friction and the (horizontal) weight of the object. It does not (to first order) depend on the contact area.

The condition for the object to slide is that the tangent of the angle equal the coefficient of (static) friction. By finding the angle where the object just begins to slide, you can find the coefficient of static friction by simply taking the inverse tangent. (This is the key on your calculator that says
tan
⁻¹
,
arctan
or
atan
.) See
Figure 29-1
.

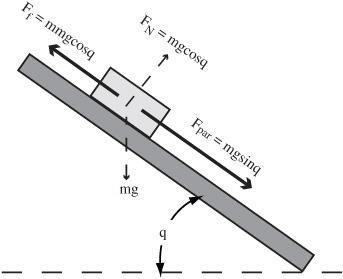
Figure 29-1
Forces on an incline
.

Friction applies a force that puts the brakes on motion. The amount of friction between two surfaces is characterized by something called the coefficient of friction, which is represented by the Greek letter μ (mu pronounced “myoo”). On a horizontal surface, the force exerted by friction is equal to the weight of the object, multiplied by the coefficient of friction. There are two types—static friction, which must be overcome to get something going, and kinetic friction, which must be overcome to keep something going.

In this project, the objects slide down the ramp if the tangent of the angle is greater than the coefficient of static friction for that object on the book. This condition can be turned around and, if the sliding angle is found, the coefficient of friction can be easily and simply determined.

A follow-up along a similar theme is to predict whether an object can slide along a surface without toppling. A book sliding front side down on a smooth table will not have stability problems. But a can of tomato juice sliding upright across a rough wooden floor may be another story. Try this with several cylinders with the same diameter, but with different heights. Sections of cardboard tubes or plastic pipe sections are good to test this. The condition for sliding without tipping is that the coefficient of (kinetic) friction be less than the ratio of the diameter of the cylinder to its length.

You could also design an experiment to study the effect of increasing the weight, surface area, and velocity of motion. You will find the weight of the object is the only significant variable and (surprisingly, for many people) the contact area is (almost entirely) insignificant.

Friction
is a force that opposes motion. On a horizontal surface, the amount of friction depends on the weight of an object pressing it in contact with that surface, and the coefficient of friction.

The force exerted by a spring, unlike any of the forces we have encountered so far, is not constant. It continuously varies. The further you pull the spring, the harder it pulls back. This relationship is known as
Hooke’s law
. Because of this, springs have the capability to keep going back and forth until friction (eventually) slows them down.

• various springs
  
• mass set (or a spring scale)
  
• metric ruler
  

Measure the spring constant of a spring by following these steps:

1. Suspend the spring from the support.
   
2. Locate the distance from the bottom of the spring just hanging under its own weight. This is called the
   equilibrium point
   .
   
3. Hang a mass from the spring. The mass should be chosen so it increases the length of the spring by no greater than about 50 percent.
   
4. Measure the distance (in centimeters) the bottom of the spring is pulled below the equilibrium point. See
   Figure 30-1
   .
   
5. Find the force. If your reading is in grams, convert it to newtons by dividing the mass in grams by 1000 to get kilograms, and multiplying by 9.8 to get force in newtons. It may be easier to do this using a spring balance to get the force to pull the spring a certain distance. Many spring balances are calibrated directly in newtons, so in that case, there is no need to convert the force into newtons.
   
6. The spring constant can be determined by dividing the force by the distance according to the equation: k = −F/x. (Note: the negative sign accounts for the fact that the force and the extension are in opposite directions. If you pull up, the distance is positive, but the force is negative. Regardless of how you do it, the spring constant is
   always positive
   .)
   

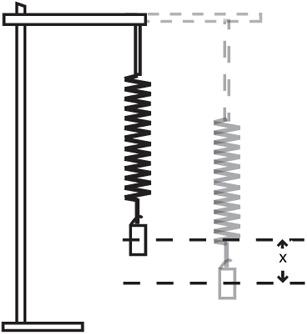
Figure 30-1
Determining how stiff a spring is by measuring the spring constant
.

The stiffer the spring, the higher the spring constant. As an example, if it takes 10 newtons of force to stretch a spring by 1 centimeter, the spring constant would be k = 10N/1cm = 10N/cm. It would take 20 newtons to stretch that same spring by 2 centimeters. The spring constant should prove to be constant and establish a linear relationship between force (F) and extension (x). Real springs have a linear range over which Hooke’s law is a reasonable approximation. If you stretch too far, however, you will go out of the linear range and it usually takes an initial force to bring the spring into its linear range.

Over most of its range, the force exerted by a spring is directly proportional to the amount it is displaced from its equilibrium position. The spring constant is a way to characterize how much a particular spring exerts for a given displacement from equilibrium.

A more accurate value for the spring constant can be determined by taking several readings and plotting force versus displacement, and then finding the slope of the line.

The force exerted by a spring is proportional to the distance the spring is stretched. The further you pull, the greater the force the spring exerts in the opposite direction.

The Atwood machine illustrates some aspects of force and acceleration. Like an incline, the Atwood machine slows acceleration down to a measurable and observable amount. This project shows how the Atwood apparatus can be used to study acceleration.

• pulley
  
• support for pulley, such as a ring stand
  
• string
  
• various masses
  

1. Set up the apparatus with each of two masses attached to string and suspended over a pulley, as shown in
   Figure 31-1
   .
   
2. Release the masses and observe/measure their motion.
   
3. As in previous experiments, the acceleration of the masses can be measured using the stopwatch method (using a = 2d/t
   ²
   ) or determining the acceleration using a motion sensor. (Different combinations of masses can also be compared and ranked visually without detailed measurements.)
   

The greater the difference between the two masses, the greater the acceleration.

The greater the combined masses, the smaller the acceleration.

The acceleration for the two masses is:

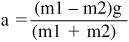
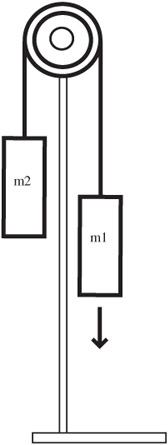
Figure 31-1
Atwood’s machine
.