125 Physics Projects for the Evil Genius (9 page)
Read 125 Physics Projects for the Evil Genius Online
Authors: Jerry Silver

First, you measure what is the best angle to aim something for it to travel the greatest distance.
Then, you make and test predictions. To hit a target, you need to know only two things: the
velocity
of the projectile and the
angle at which
it is shot. That’s all. Knowing only those two conditions, you can determine how far the projectile will go, and how high it will go. The angle is easy to measure directly, so we will first work on a simple way to determine the velocity.
- projectile and launcher
– A projectile launcher, such as shown in
Figure 9-1
. Plastic rather than steel balls are safer.
– Or, a toy gun, a toy bow-and-arrow, a ping-pong ball shooter, Nerf gun, or a marble launcher.
- tape measure
- protractor
- target—horizontal: pan or cup; vertical: ring on a ring stand
- stool(s) or other moveable object to hold the target at the height of the launcher
What is the best angle?
We start here because this part does not involve any number crunching.
1. You will be shooting your projectile from ground-to-ground or from table top to raised surface at the same height as the table top. The projectile should be launched and land at the same height.
2. Select a setting for your launcher that will fire a projectile from a given height and return to that same height without hitting the ceiling, a wall, or breaking anything.

Figure 9-1
Projectile launcher. Courtesy PASCO
.
3. For every test in this part, you will be using the same velocity. Pick an angle to shoot the projectile at. Launch the projectile and measure the distance. Increase or decrease the launch angle until you find the angle that gives the greatest distance. (Remember, for this part, we are measuring the distance the object goes after returning to the same height from which it was launched.)
Determine the velocity of the launcher (to make predictions).
For this part, we are going to use the method of the previous section to determine how fast the projectile is moving as it leaves the launcher.
For this part only
, we shoot the projectile
horizontally
, so we can find this velocity.
- Fire horizontally several times and record the distance,
R
, that the projectile travels (in
m
). Take the average. - Measure the height when the projectile leaves the table.
- As we did in the previous experiment, we will use the trick of
finding the time the projectile is in flight
by determining how long it takes to fall. This can be simply found just knowing the height (in meters) and using the equation, t = (2d/g)
½
, where
g
is 9.8 m/s
2
.
Table 8-1
in the previous section gives the time,
t
, for various heights. - Now, it is a simple matter to
find the velocity
using the technique of the previous section. Divide the distance the object goes along the floor,
R
(in meters), by the time it was in flight,
t
(seconds). This is given by the formula:
Hitting the targetv = R / t
1. Select an angle, θ, at which you will shoot the projectile.
2. Predict the range, or how far the projectile goes along the floor, using the equation
R = (v
2
/g)sin2θ
where
v
is the velocity you just found in number 4,
g
is 9.8m/s
2
, and θ is the angle you selected.
3. Predict the height using h = (vsinθ)
2
/2g, with the variables as defined in the previous equation.
4. Set a cup a distance
R
horizontally along the ground located at the same height as the launcher.
5. Set a ring on top of a ring stand at a height,
h
, above the level of the launcher. The circular opening of the ring should be facing the launcher. Use a few stools (stacked on top of each other, if necessary) to set the ring stand to establish the height target.
6. Visually align the targets, so they are in line with the projectile.
Expected Results7. After you set the targets to where you predicted they should be, fire the launcher and see how close you get.
Figure 9-2
shows typical results for a projectile fired at a velocity of 10 meters per second. Notice that the 45-degree angle results in the longest range. Notice also that the 60-degree and 30-degree angles wind up in the same place. The projectile fired at 75 degrees stays in the air longer, but it has a lower horizontal velocity than the one fired at 30 degrees.

Figure 9-2
Projectile shot at 10 m/s, returning to the same height it was shot from
.
According to the range equation:
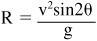
a 45-degree angle gives the greatest distance an object moves horizontally along the ground. For a given launch velocity and a chosen angle, the range a projectile will go can be determined.
Similarly, the height equation
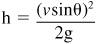
determines the maximum height of a projectile, given the launch velocity and the chosen angle.
Combining projectile motion with “thermodynamics:” OK. The justification for doing this, other than for fun, is a stretch. But it does add a bit of extra excitement to this experiment. To do this, first of all, find a very safe place away from ceilings, loose paper, or any flammable object. Nothing flammable should be underneath the ring in case of drips. Wrap the ring with a small amount of tissue paper and soak it in a little alcohol. By carefully igniting the ring, you can shoot the projectile through a flaming ring. Careful means: wear safety glasses, use a long wooden match, and make sure that neither you nor any viewers come in contact with the flame or the ring immediately after it burns because it can remain hot for a short while. This can be made even more dramatic in a very corny way by playing a recording of Johnny Cash’s “Ring of Fire.” This must be done in a safe place and under the supervision of an adult (if you are not yet an adult). By the way, this experiment does work perfectly well with a nonflaming ring.

Figure 9-3
T. Dragoiu shows the “ring of fire” top-of-trajectory target for a projectile shot at an angle
.
Another much simpler but less accurate way to launch a projectile with a known velocity at a predictable angle is to drop a bouncy ball from a consistent height from an incline. The ball will come off at various angles, depending on the slope of the board. As a result of conservation of mechanical energy, if released from the same height above the board, the ball will bounce off at the same velocity. This may not go as far, but it provides a lower cost option to produce a reasonably constant velocity at various angles.
The range and height of a projectile can be determined from knowing
only the following two things: velocity
of the projectile and the
angle
that it is launched from.
Monday night football. Tracking the trajectory
.
This experiment will take you outside to make these measurements. You can also collect data from Monday night football.
The measurement part is very simple. All you need to measure is the
total time a ball or other projectile is in the air
and the
total distance along the ground
that the projectile travels. If we measure only those two things we can figure just about everything else: launch angle, velocity, and height.
How high did the punt go? How hard was the ball hit? What angle did it go? You kick a soccer ball, hit a golf ball, and punt a football. Which has the greater velocity? Without resorting to a high-tech solution, such as a radar gun, there is a simple way to answer that question using only the laws of motion.
To do this, you either work the calculations or use the tables as a guide—your choice.
- stopwatch
- football field
- TV tuned to a football or baseball game
- assorted projectiles and launchers: soccer ball or football; tennis ball and racket; golf club and ball
- Launch the projectile and, at the exact same time, start the stopwatch.
- Record how far the object goes and how long it was in the air.