125 Physics Projects for the Evil Genius (29 page)

Equilibrium is maintained when the center of mass is centered over the area of support.

How far can an object tilt before it falls? Like the Leaning Tower of Pisa, the stability of a rectangular or cylindrical object depends on its shape. This experiment establishes a simple condition for stability of an object and explores the idea of center of mass.

• cereal box
  
• pizza box
  
• 2 pencils
  
• tape
  
• string
  
• 2 nuts, large washers, or other matched attachable weights
  
• wooden board to use as an incline (roughly 3 ft × 4 inches × ½ inch, or 1m × 0.1m × 0.01m)
  

1. Find the center of each of the rectangular faces of the box.
   
2. Start with the largest face first. Push one pencil through both sides of the box. The pencil should be roughly perpendicular to the surface it is pushed through.
   
3. Tie the string—one end to the pencil and the other end to the hangable weight.
   
4. Attach the other weight to the other side of the pencil as a counterbalance. You can use string if that makes this easier.
   
5. Tape the other pencil across the incline, somewhere roughly near the midpoint.
   
6. Place the box on the incline, so the downhill side of the box is in contact with the pencil taped to the incline. This pencil serves as a pivot point to force the box to rotate, rather than slide down, the incline.
   
7. Make your predictions. How far can you lift the incline before the box topples?
   
8. Try this with the various faces of each of the boxes. Can you develop a general condition for stability?
   
9. You can do this qualitatively as discussed previously or take it a step further and relate the geometry of the box to the angle it can tilt at and still be stable. Can you predict the maximum angle of stability for given box dimensions?
   

The box will be stable if the center of mass (marked by the pencil) is over the base of the box in contact with the incline. Once the angle increases to the point where it is outside the base, the object will rotate.

Objects are more stable when the center of mass is closest to the incline.

Because a pizza box has a square-top face, it will be stable up to a 45-degree angle when propped up with one of the long edges placed along the incline, as shown in
Figure 47-1
.

Figure 47-1
The leaning tower of “pizza.”

If A is the length of the side of the box in contact with the incline and if B is the height of the box (for that particular arrangement) above the incline, the maximum stable angle is given by: tangent (angle) = A/B. (The angle can be found by taking the inverse tangent or
arctan
, which can be found on most scientific calculators.)

For instance, a 17-ounce box of Honey Nut Cherrios has dimensions 12 inches × 7 ¾ inches × 2 ¾ inches. The six possible placements for this box are summarized in
Table 47-1
.

A few of these are illustrated in the following
Figures 47-2
,
47-3
, and
47-4
.

Massive objects tend to act as if all their mass was concentrated in a single point called the
center of mass
. Gravity pulling on that point causes the box to rotate about the pivot point established by the pencil. If the center of mass is above the base of support, the object tends to rotate in such a way as to remain stable on the incline. However, as the center of mass moves out from above the base, a torque is applied, which tends to rotate the object, so it rolls down the incline.

This approach can be easily extended to other shapes. You can cut a cardboard tube at an angle near the bottom edge to form a replica of the Leaning Tower of Pisa (not necessarily to scale). Try to cut it in such a way that the tube remains standing at the minimum possible angle with respect to the ground. This would make a fun challenge for a group. This can be done either by trial-and-error or by calculations based on an approximately rectangular cross-section. By the way, the real Leaning Tower of Pisa is currently tilted at 5.6 degrees and would topple if that angle increased 1.4 degrees, according to a tilt angle of 7 degrees (Rossella Lorenzi, Discovery Channel Online News
www.discovery.com
, September 1998,
http://www.endex.com/gf/buildings/ltpisa/ltpnews/ltpdisc092298.htm
). The mass distribution of the Leaning Tower of Pisa is not strictly that of a cylinder and currently benefits from various techniques of shoring it up.

Table 47-1

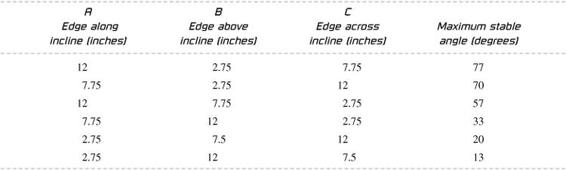
Figure 47-2

Figure 47-3

Figure 47-4

By the same token, you can cut cardboard mailing tubes in 3″, 6″, 9″, and 12″ lengths. Then, place them on a board with a stop to keep them from sliding. As you tilt the board, each of the tubes will topple in sequence, starting with the tallest.

Objects are stable if their center of mass is within their base of support.

Energy is neither created nor destroyed; or as physicists say, energy is always conserved. This project is a test in one’s confidence in this time-honored principle. This experiment can be done with any size pendulum. However, a large pendulum with a heavy mass raises the stakes and increases the suspense.

• pendulum
  

– mass: consisting of any mass that can be
securely
supported (such as a hooked mass or a bowling ball)

– string or cable strong enough to support the mass

– secure overhead support such as a ceiling beam that can safely handle the moving mass

• fragile object you do not want destroyed by the pendulum. You may want to start with a plastic bottle before attempting this on your more expensive pottery.
  

1. Set up the pendulum, so it swings freely.
   
2. Set an object in the path of the pendulum.
   
3. Position the pendulum mass, so it is between the object and the equilibrium point, and
   just
   touching the vase.
   
4. Release, but don’t push
   the pendulum mass from its point of contact with the object.
   
5. Let the pendulum go through a full excursion from where it was released, and then back.
   

If the mass was released and not pushed, it will never go higher than the point from which it was released. The pendulum will return to, but never exceed, the release point.

For people who are still in the process of developing a sense of confidence in the law of conservation of energy, a moment of suspense may exist as the pendulum returns to its original height. In any real pendulum, there is a certain amount of friction in the point of contact and from air resistance. Because of this, the pendulum returns to a point
slightly lower
than the point from which it was released from.

Figure 48-1
What goes down, must come up (to
almost
the same height that it was released from)
.

The potential energy of an object is equal to its weight times the height it is raised to. For objects released from rest, as is the case here, there is no starting kinetic energy. So, the amount of potential energy you start with equals (or is slightly lower than) the final kinetic energy. The pendulum will never quite return to the level that it was released from because some energy is “lost to” friction as the mechanical energy is transformed into thermal energy.