125 Physics Projects for the Evil Genius (30 page)

A variation on this involves the related idea of
conservation of angular momentum
. If you release a pendulum in such a way that it does
not
hit the vase, no matter how many times it swings back and forth, it will
not
hit the vase.

The amount of energy contained in a moving object, such as a swinging pendulum, can neither be created nor destroyed.

This experiment compares how much energy an object has after following several different paths. We can determine how much energy a ball has after rolling down an incline by measuring how far it rolls off a table.

• 2 inclines supported by a ring stand or a stack of books (one incline that works well with golf balls is a vinyl bullnose section of molding available at home supply stores)
  
• 2 golf balls or other matched objects to roll down the incline, such as marbles, coffee cans, toy cars, or a air track glider
  
• meterstick or tape measure
  
• optional: motion sensor
  

1. Set up the inclines at two different slopes, as shown in
Figure 49-1
. Allow enough space at the bottom of the incline so that the golf balls roll off the table horizontally.

2. Avoid an angle that is so severe as to cause the golf balls to bounce on the edge of the table.

3. Align the inclines so they are pointing in the same direction.

4. Hold the two golf balls at equal height above the table. This may be easier with two people.

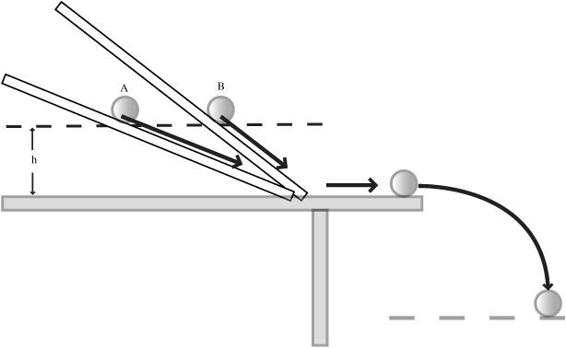
Figure 49-1

5. Predict what you think will happen with each of the balls. Which will come down with the greatest velocity? The velocity can be determined either by using a motion sensor or by comparing the point that it hits the floor after rolling off the table.

6. Release both golf balls and compare the results with your prediction.

Both balls should move with the
same velocity
, as they roll horizontally across the table. The balls then hit the floor at the
same distance
from the edge of the table.

In this, as in all other projects, energy is conserved. The energy each of the two golf balls starts off with is the same because they are released from the same height. This is equal to the object’s weight times gravitational acceleration. All of this energy is converted to kinetic energy (neglecting frictional losses) when the balls get to the bottom of the incline. With
equal kinetic energy
, the objects will move at the
same velocity
.

Pick one of the slopes and hold a golf ball on the incline at each of three different places (for example at 6-inch intervals starting from the top of the incline). Predict the outcome. Release the ball from each of the three positions and compare the results with your predictions. Here, the ball starts with three different amounts of potential energy. It comes off the incline with three different velocities, as shown in
Figure 49-2
. According to the law of conservation of energy (neglecting friction), the potential energy (mgh) is converted to kinetic energy (½ mv
²
). The distance that a horizontal projectile travels is proportional to its horizontal velocity. As a result, the range or
distance
along the floor will go as the
square root
of the
height
above the table.

Total mechanical energy (consisting of kinetic and potential energy) is conserved unless some energy is consumed in overcoming friction. Objects released from the same height have equal potential energy. When this energy is converted to kinetic energy, the path the objects move toward the bottom is not important.

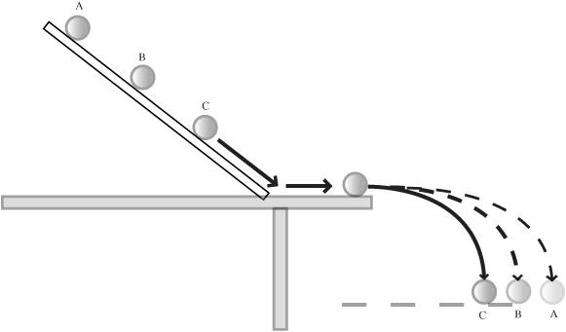
Figure 49-2

Which path will take the least amount of time for a rolling ball?

• a path that is straight and horizontal, or
  
• a longer path that starts horizontally, dips in a curved path without excessive friction, and then returns to the same horizontal level it started from.
  

One path is shorter. So you might think it will take the least amount of time. Because both objects return to the same height, they wind up with the same amount of energy. How does that affect the overall time for the journey?
Figure 50-1
shows the two paths.

• 2 golf balls
  
• materials to build a track:
  

– flexible flat wooden molding—one section 8 feet long and one section 6 feet long

– a side board about 6 feet long

– a couple of 2″ × 4″ × 6″ pieces to serve as a base

– small flat-head wood screws

– small wooden or metal right-angle braces—1 inch corner molding will work

– optional—a basket or plastic cup

• This type of apparatus is also commercially available, as shown in the later
  Figures 50-6
  and
  50-7
  .
  

1. Draw or sketch the shape of the curved section. This can be traced, copied, or eyeballed. A more exacting approach would be to generate a geometric cycloid and form the curve into that shape.

2. Attach the flexible track to the side board with a straight section, a downward curve returning to a second straight section. Attach the braces to the side board and secure the flexible track to the braces. (Keep the profile of the screws as low as possible, so it does not interfere with the motion of the golf ball. It may be necessary to countersink the screw hole, so the screw head is below the level of the track.)

Figure 50-1
Both ball start at the same height. Courtesy Dan Silver
.

3. Attach the straight section to the side board, a few inches above the section with the detour.

4. Attach the base in such a way that the path the ball will follow is slightly tilted toward the side board. This minimizes the friction the ball encounters, but it will allow the ball to roll without falling off the track.

5. You may want to add some way to catch the balls after each race to avoid having to chase them every time.

6. A ramp of equal slope and equal length is placed at the start of each path to give objects racing down the two paths the same starting velocity. Be sure to keep any seams in the track as low profile as possible.

1. Before doing this, observers can make their prediction. Which track is fastest: a) the flat track b) the track with the detour c) both the same?
   
2. Release both balls from the
   same height
   (above the initial flat section of track) at the same time. Observe the progress of the balls. Repeat a few times to make sure the results are consistent.
   

At the end of the track, regardless of which ball finishes before the other, measure the velocity on the final flat section. You can do this in several ways:

1. Use a motion sensor to measure the speed of the balls on each of the flat sections. If you have two motion sensors, you can measure them at the same time. If you have one, you can do them one after the other. In either case, the most definitive conclusion will result from a good statistical sample.
   
2. Another way to measure velocity is to take advantage of the fact that the range of a horizontal projectile (as you saw in
   Project 6
   ) depends only on its height above the ground and the velocity with which it leaves the horizontal surface. In the apparatus shown in
   Fig 50-1
   it is clear that the starting and stopping level for each of the tracks is at a different height above the ground. This does not affect their movement relative to each other. However, it does give the track on top an advantage where it will land unless the height difference is compensated for by raising the landing level. If this is done, balls that move the same distance along the ground have the same velocity. Some designs such as a track used at Michigan State University (
   http://demo.pa.msu.edu/PicList.asp?DID=DID18
   ) are built with the two tracks side-by-side, so this velocity comparison can be made more easily. Plans for a similar racing-ball track are available from the University of Maryland Physics Department at
   http://www.physics.umd.edu/deptinfo/facilities/lecdem/services/demos/demosc2/c2-11dwg.jpg
   .
   

The ball on the flat track will move with constant velocity (
Figure 50-2
).

The ball following the detour will increase its speed, so it is going fast enough to make up for the extra distance (
Figure 50-3
).

Once returning to the original height, the ball that went through the detour will return to its original speed. However, now it will be ahead of the ball on the flat track. The ball on the detour will reach the end of the track first (
Figure 50-4
).

Figure 50-2
Both balls begin with the same velocity. Courtesy Dan Silver
.