125 Physics Projects for the Evil Genius (41 page)
Read 125 Physics Projects for the Evil Genius Online
Authors: Jerry Silver

A variation on this is to attach a force gauge to the spring to track the force along with the motion of the pendulum.
Physics alert: Those of you familiar with calculus will recognize that velocity is the first derivative of distance. Acceleration is the first derivative of velocity and the second derivative of the distance with respect to time. If the distance follows a sine curve, the velocity (the first derivative) is a cosine curve and the acceleration is a sine curve.
A
spring
is a simple harmonic oscillator whose distance follows a sine wave pattern. Velocity and acceleration follow a similar shape, but are delayed with respect to the distance curve. The velocity is at a maximum at the point of the greatest displacement. Acceleration is at a maximum at the point of greatest extension.
Natural frequency
.
When you push someone on a swing, timing is important. If you push just as the swing has come to its highest point and is ready to begin its return, you will keep the swing going and increase its amplitude. However, if you push randomly, your efforts will be far less effective and, at times, you will tend to slow the motion of the swing. The reason for this is a swing has a natural frequency. If your pushing is at the natural frequency of the swing, the swing will resonate. This experiment explores the idea of resonance.
- 2 ring stands
- 1⅜ inch diameter wooden dowel, 12 inches long
- 2 clamps (to hold the dowel)
- string of various lengths, from about 3 inches to 10 inches
- set of several small masses that can be attached to the string (large stainless steel nuts work well here or any attachable masses in the overall range from 10–50 g)
1. Tie loops at one end of each of the strings and tie the other end to a mass. At least two of the strings should be the same length. The other should be random—some larger and some smaller than the matched pair. Avoid, however, having all the other strings half or double the size of the matched pair.
2. Slide the loops onto the dowel and spread the strings out evenly across the length of the dowel. The two matched strings should not be next to each other.
3. Attach the dowel to the two upright posts of the ring stands using the clamps. Leave enough space, so all the masses are free to swing without hitting the table, which the ring stands are placed on. The dowel should be slightly flexible, but constrained by the ring stands, so it will not sway or swivel when the masses are swinging. See
Figure 69-1
.
4. Steady all the masses hanging on the strings.
Expected Results5. Take only one of the masses on the matched strings and displace it, so it is swinging perpendicular to the direction of the dowel.
What we want to see here is for the stationary string, which is the same length as the one that was set in motion, to also start moving back and forth. The other masses might jostle around a bit, but they should not be set into a significant swinging motion.
The resonant frequency of a pendulum is determined exclusively by the length of the string that supports it. The stationary pendulum is stimulated by the swinging pendulum that has the same length and, therefore, the same natural frequency.
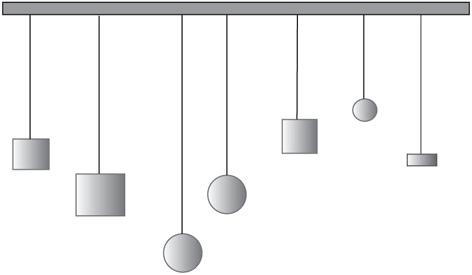
Figure 69-1
Resonant frequency depends only on string length
.
Other questions that can be addressed are:
1. Would a pendulum with the same string length, but different mass, have the same resonant frequency as the swinging pendulum?
The Point2. What if we throw in a few harmonics? What is the response of a pendulum that is one-half the length of the swinging pendulum? What is the response of a pendulum that is double the length of the swinging pendulum?
A simple harmonic oscillator, such as a swinging (simple) pendulum, has a natural frequency. If stimulated at that natural frequency, the amplitude of that pendulum will be greatest.
Bunsen burner pipe organ. Resonant frequency
.
If you blow across the top of a soda bottle, you produce a sound. The more soda you drink, the deeper the pitch of the sound. This is because the resonant frequency of the bottle increases as the height of the air above the liquid increases. This project does the same thing, except on a much bigger scale. You use longer tubes that produce deeper sounds. You may just want to give the person who is responsible for the building you are in (such as the building principal) advance warning that the sound they will be hearing is not an earthquake, not a water buffalo in labor, and not the propulsion system for a space alien spacecraft.
- large Bunsen burner
- cylindrical tubes roughly 0.8–2 meters in length—good candidates for this are cardboard tubes used for carpet rolls or hollow metal sections of old driveway basketball backboard supports
- fire extinguisher and/or bucket of water (you should
not
need this, but just in case)
- Place the Bunsen burner on the floor.
- Route a hose long enough not to get tangled and connect it to a natural gas outlet (which, at this point, is not turned on).
- Position a cylindrical tube on the floor, so it can easily be placed over the burner.
- Light the burner and adjust it, so the flow is maximum, with the greatest flame.
- Make sure nothing flammable is near the burner, including possible objects on the ceiling and loose papers that might inadvertently be drawn into the flame by convections.
- Lift the cylinder with both hands and position it above the burner. Hold it a few inches above the top of the burner, but not so low that it constricts the air going into the burner. See
Figure 70-1
. - Be somewhat careful to avoid charring the edge of the tube. Do not hold the edge of the tube directly over the flame. If held correctly, the tube will not burn. Also exercise similar care to avoid excessively heating a metal tube, which could possibly result in a burning hazard.
- It may take as much as a minute or so until a sufficient stream of exhaust from the Bunsen burner flows through the tube to produce an acoustic resonance.
- Measure (or, if you prefer, observe) the pitch (or frequency) of the sound produced using the pitch gauge or oscilloscope. You can also compare the pitch with a known frequency, such as produced by hitting a tuning fork or sounding a musical instrument.
- Remove the cylinder and don’t forget to turn off the burner when you are finished.

Figure 70-1
Resonating tube
.
With a sufficient flow of heated air, the tube should resonate. The taller tubes produce a much lower pitch than the shorter tubes. The diameter of the tube does not affect the pitch, but it may affect the volume by impacting how much air can flow.
For a given length, the frequency of the tube is given by:

The shorter columns produce tones consistent with the sounds of common concert instruments. The longer columns produce very deep, resonant pitches.
The flowing air, just like a wind instrument, creates a resonant standing wave in the tube. The longer the tube, the longer the wavelength, but the shorter the frequency.
The frequency for an open tube is given by f = v/2L. For a given tube length, this frequency is twice as high as it would be for a closed tube. Refining this to take into account the slight offset of the node from the ends of the tube, the equation is:
f = v/2(L + 0.8d)
where
d
is the diameter of the tube (in m),
L
is the length of the tube (in m), and
v
is the speed of sound (in m/s).
If you have more than one tube whose diameters are similar, you can nest several tubes together, one inside the other, as shown in
Figure 70-2
. This can let you continuously vary the pitch of the tube, like a trombone. You may want to practice before auditioning for the spring musical.
The resonant frequency in an open pipe is lower for a greater length.

Figure 70-2
Changing the note like a trombone
.
Springs and electromagnets. Resonance
.
On one side of the room, you have a bar magnet suspended from a spring. The magnet is surrounded by an electrical coil, which is attached to another coil on the other side of the room. An identical magnet is placed inside the second coil. As the first coil starts moving, an electrical current is produced, which also causes the second magnet to start moving. This is impressive to see and demonstrates several principles of physics, including resonance, magnetic induction, and magnetic force.
- 2 bar magnets
- 2 equal springs
- 2 wire coils with an interior opening just large enough for the magnets (these can be made or are available from scientific equipment supply companies)
- 2 ring stands with clamps to support a horizontal connecting bar; 2 pendulum clamps would be perfect
- string
- table
- connecting wire
- optional: 4 LEDs