Collected Essays (65 page)

Rudy holding a cone shell with a gnarly cellular automata pattern

To summarize, my original dialectic argument says:

Thesis:
Everything is a computation.

Antithesis:
Human consciousness doesn’t feel like a computation.

Synthesis:
Everything is a gnarly computation.

And this argument takes us from my statement (1) to my statement (2).

What is Gnarl?

By way of explaining more precisely what I meant by a gnarly computation, I’ll point out that computations lie on a spectrum of complexity. My analysis follows that of Stephen Wolfram in his book,
A New Kind of Science
, [Wolfram 2002].

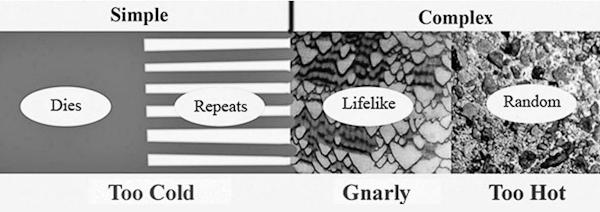
The spectrum of computational complexity

Suppose that we focus on some particular category of computations such as Turing machines or cellular automata rules. No matter what the category, we always find four basic kinds of behaviors: comes to a halt; goes into a repeating loop; produces unpredictable but somewhat orderly output, produces random-looking output.

We view the first two types of behavior as simple, and the second two types as complex. In chaos theory, both of the complex classes are regarded as chaotic. The reason I have introduced the word “gnarly” for the third class is so as to have a more convenient phrase than “somewhat orderly chaos.” Christopher Langton refers to this zone as the
edge of chaos
.

In this context, we aren’t very interested in the distinction between the terminating and repeating computations, so we lump those two simple classes together. Thus we arrive at three general classes: simple, gnarly, and random-looking. And just as in the fairy tale about Goldilocks and the Three Bears, we can view the behaviors as too cold, just right, and too hot.

Simple
(Too Cold): Dies Out or Repeats.

Gnarly
(Just Right): Complex, moving, unpredictable. Life. Natural processes.

Random-looking
(Too Hot): Seething.

Most of my own taxonomic research on computations has centered on two-dimensional cellular automata. We can think of these computations as taking place on a computer screen. Each pixel acts as a tiny independent computer, each pixel updates its state on the basis of the states of its neighboring pixels, and the states are depicted as colors.

At the end of his life, the computer science pioneer Alan Turing was beginning to use these kinds of rules to show how the patterns on animal coats and butterfly wings might emerge from cellular automata rules based on two competing chemicals, an activator and an inhibitor. The “Turing patterns” that emerge from these rules can look like spots or filigrees.

Nine gnarly cellular automata

We can create computer simulations of these rules by supposing that the state of each pixel includes two real numbers representing the intensities of activator and inhibitor. Figure 23 shows some of the patterns generated by these rules. In these images we see the spontaneously generated scrolls that biochemists call Belousov-Zhabotinsky scrolls. The dynamics of these patterns are lovely. The spirals are constantly turning, and the scrolls expand, swallow each other, and spawn off new scrolls—almost like living creatures.

Getting back to my main line of argument, let me say a bit more in my support of my statement (2): Every object or process is a gnarly computation. In many cases it’s intuitively clear that nature is performing a gnarly computation: think of swaying trees, a flickering fire, the cracks in drying mud, flowing water, or even a rock. A rock? To the human eye, a rock appears not to be doing much. But viewed as a quantum computation, the rock is as lively and seething as, say, a small star. At the atomic level, a rock is like a zillion balls connected by force springs, and we know this kind of compound oscillatory system behaves chaotically.

Panpsychism

For the next stage of my argument, I want to argue for a form of what Wolfram calls the
Principle of Computational Equivalence
. This is my statement (3): Every naturally occurring gnarly computation is a universal computation.

Computer scientists define universal computers as systems capable of emulating the behavior of every other computing system. The complexity threshold for universal computation is in fact very low. Any desktop computer is a universal computer. A cell phone is a universal computer. A Tinkertoy set or a billiard table can be a universal computer. And very many gnarly computations such as Conway’s Game of Life have been proved to be universal computations as well.

One difficulty here is that in 1956, Richard Friedberg and Albert Muchnik, working independently, showed that one can in construct computations which are gnarly but not computation universal. This is why in my version of the Principle of Computational Equivalence, I restrict the focus to “naturally occurring computations”—the supposition being that the Friedberg and Muchnik computations are in fact so artificial as not to occur in the wild.

Now we come to the question of consciousness. On the surface, being a universal computation seems like very nearly a sufficiently strong condition for being conscious. But there is a sense that one’s consciousness has something more, and one might well suppose this additional ingredient to be self-reflection, where the self-reflection aspect of a system stems from having a feedback process whereby the system has two levels of self-awareness: first, an image of itself reacting to its environment, and second, an image of itself watching its own reactions. (See [Damasio 1999].) Thus we arrive at statement (4): Consciousness = Universal Computation + Self-Reflection.

I have come to believe however that the requirement of self-reflection is otiose. That is, my experience as a computer scientist suggests that one can in fact used fixed-point methods to give any universally computing system this kind of self-reflectivity. This leads to my statement (5): Any complex system can be regarded as having self-reflection.

And thus we can deduce (6):
Panpsychism
. Every physical entity is conscious.

One problem which remains to be solved is whether we can learn to converse with the conscious objects surrounding us. Possibly we will develop some quantum computational technique so that one can sufficiently entangle oneself with an object so as to able to talk with it.

Hylozoism

My fellow philosopher of computer science, John Walker, makes the point that living beings seem to have memory as well as universal computation. (See [Walker 2004].) Walker points out that humans, for instance, have physical memories at three different levels.

Genetic memory
: DNA.

Organic memory
: Immune system.

Behavioral memory
: Neural patterns.

Even if we don’t expect living entities to have a biological component, one can make a case that memory plays an essential role in such characteristically life-like processes as reproduction, morphogenesis, and homeostasis.

Thus we arrive at (7):
Walker’s Thesis.
Life = Universal computation + Memory.

So now in order to extend my line of thought to reach hylozoism, I need some way of asserting that every physical object already has some kind of memory.

While preparing this paper to present in Kyoto, I started thinking of the Zen koan of the flag. Two monks are looking at a flag fluttering in the wind, and this system is performing a gnarly and therefore universal computation. But what
is
the system? The first monk says, “The flag is moving.” The second monk says, “The wind is moving.” The third says, “Mind is moving.”

The flag koan is, in its own way, a dialectic triad, and the flag/wind system is a conscious mind.

That is my panpsychic interpretation of the koan; probably the more common interpretation is a pantheistic one, under which the flag/wind motion is viewed as an aspect of a single, overarching mind that imbues all things.

Now suppose we want to say the flag/wind system is alive as well. Does the fluttering flag have a memory so as to satisfy Walker’s thesis? At first it seems the answer must be no. An isolated natural system is dissipative, that is, different past histories can lead to identical present states.

In my novel
Hylozoic
, I suppose that we might get around this problem by changing the topology of space at scales below the Planck length—that is, below the size scale at which our current notions of physics break down.

The current notion of space at very small scales, taken from string theory, is that we have a lot of extra dimensions down there, and that most of them are curled into tiny circles. But what if we could find a way to change the intrinsic topology of space, uncurling one of these stingily rolled-up dimensions? Of course we’d be careful to pick a dimension that’s not absolutely essential for the string-theoretic Calabi-Yau manifolds that are supporting the existence of matter and spacetime. Just for the sake of discussion, let’s suppose that it’s the eighth dimension that we uncurl.

I see our eighth-dimensional coils as springing loose and unrolling to form infinite eighth-dimensional lines. This unfurling will happen at every point of space. Think of a plane with hog-bristles growing out of it. That’s our enhanced space after the eighth dimension unfurls. And the bristles stretch to infinity.

And now we’ll use this handy extra dimension for our universal memory upgrade! We’ll suppose that atoms can make tick marks on their eighth dimension, as can people, clouds, or stones. In other words, you can store information as bumps upon the eighth-dimensional hog bristles growing out of your body . The ubiquitous hog bristles provide endless memory at every location, thereby giving people endless perfect memories, and giving objects enough memory to make them alive as well. (Do understand here that I’m speaking in a completely speculative and fanciful way.)

Is there any less science-fictional way to achieve the same result? One approach might be to say that there are in fact no isolated natural systems. The effects of the flag/wind system’s state ten minutes ago are still present in the state functions of the myriads of particles that are quantum-entangled with the particles of the air and the flag. Put more simply, the system’s memory is part of the universal state function. In this once again pantheistic view, each limited system can draw upon the entire memory of the universe as a whole.

This notion is anticipated by the Zen koan in which a monk asks the sage, “Does a stone have Buddha-nature?” The sage answers, “The universal rain moistens all creatures.”

Thus we arrive at (8): Every physical entity has memory via its interactions with the universe. And now we have reached our goal of (9):
Hylozoism
. Every physical object or process is alive.

In closing, I should mention that in an earlier paper [Rucker 2008] I combined statements (4) and (7) to have this statement: Consciousness = universal computation + memory + self-reflection. And moving from there, I argued that to be a conscious physical object of this kind is essentially to be alive—so that in the end, I arrived at the same position as in the present paper: Everything is conscious and alive.