Financial Markets Operations Management (6 page)
Read Financial Markets Operations Management Online
Authors: Keith Dickinson

The bond issuer repays the bond in accordance with the terms of issue. These can be either repayable in one amount at maturity (a bullet maturity) or in stages during the life of the bond. In the latter case, redemptions may be mandatory as in the case of a sinking fund, or conditional as in the case of a purchase fund.
Sinking fund:
The issuer is obliged to redeem a specified amount of the bond within pre-set time limits, for example, it may have to purchase 10% of the issue in each of years three and four, 20% in each of years five and six and the balance at maturity (see
Table 2.15
).TABLE 2.15
Example of a sinking fund repayment scheduleABC Bonds due 2020 Issue Size USD 1,000,000,000 2016 2017 2018 2019 2020 10% 10% 20% 20% 40% USD 100,000,000 USD 100,000,000 USD 200,000,000 USD 200,000,000 USDÂ 400,000,000 Total: USD 1,000,000,000 If the bonds are trading below par, the borrower will usually buy the required number of bonds in the market. Alternatively, the bonds can be drawn by lot and repaid at par with the relevant central securities depository advising those investors whose bonds have been drawn.
Purchase fund:
The issuer is only required to buy up to a specified amount of bonds if the bonds are trading in the market at a price below par during any particular year.There is an optional element where the bond issuer sometimes has the right to accelerate repayment of the bonds in part or in whole, in which case they usually pay a premium varying with the length of time by which repayment is accelerated. The conditions under which a bond repayment might be accelerated will be specified in the terms of the bond. The term we use to describe this right is a
call option
. There is a second optional element that gives the bondholder the right to surrender the bond
back to the issuer at a price less than par. We refer to this as a
put option
. (More details can be found in Chapter 11: Corporate Actions.)
The settlement amount for purchases and sales comprises two elements:
- The market value (consideration) of the transaction. This is the face amount of the bond multiplied by the price (quoted as a percentage to par). We refer to this price as the
clean price
. - The amount of interest that has accrued and is due to the seller.
Before we explore the topic of accrued interest in more detail, the following example illustrates the calculation of the amount payable by the buyer to the seller.
In the above example we use the terms
clean price
and
clean value
and note that this represents the market value of the bond. The accrued interest has nothing to do with a market value of the bond; it is the means by which the seller is compensated for holding the bond for a particular number of days. However, the TNA does disguise the market value of the bond, and so we refer to this as the
dirty value
.
Market convention is that bonds are traded using the clean price. It is the Settlements Department's job to calculate the correct amount of accrued interest and to apply it to the transaction.
Issuers pay interest on their bonds in accordance with the terms of the issue and this can be annually (e.g. Eurobonds), semi-annually (e.g. government bonds) or, more rarely, quarterly (e.g. FRNs).
Take the example of the EDF bond traded above. Recall that we were talking about a Eurobond, which pays interest annually. We can tell on which date the interest is paid because it will coincide with the day and month shown in the maturity date (i.e. annually every 27 January). Although we do not know when Dealer A originally purchased the bond, we make the assumption that Dealer A has held the bond since the last coupon was paid. For this particular transaction, we can say that the last coupon payment date was 27Â January 2014 (and the next coupon payment date will be 27Â January 2015).
During the period from 27 January 2014 update until the above transaction was due to settle, Dealer A was entitled to benefit from the interest that was accruing on the bond. In the example above, this amounted to 225 days.
Our EDF transaction therefore accrued 225 days' interest. How, then, did we arrive at the figure of USD 143,750.00?
- The accrued interest is calculated on the face value of the bond and not on the market value of the bond.
- Interest accrues on a daily basis up until the next coupon is paid. We therefore need to know how many days there are in that coupon period. With a Eurobond, there are 30 days in a month and therefore 360 days in a year and the calculation would be:

We can therefore summarise that a US-dollar-denominated, fixed-interest Eurobond accrues interest on a 30E/360 basis. As US-dollar-denominated, fixed-interest bonds are not the only type, we need a set of rules that apply to all types.
The International Capital Market Association (ICMA), which represents members who are active in the international capital market, deals with the calculation of accrued interest in Section 250: Calculation of Accrued Interest Rules and Recommendations.
When interest starts to accrue and when it ends is covered in Rule 251.1. This states that: “The number of days accrued shall be calculated from and including the date of the last paid interest coupon or the day from which interest is to accrue for a new issue, up to but excluding the value date of the transaction”.
3
Let us apply this rule to the example of the EDF transaction above. The last coupon payment date was 27 January 2014 and therefore the 27th represented one day of accrued interest, with a total of four days for that month. The settlement date was 12 September 2014 and therefore there were 11 days of accrued interest (as we exclude the 12th). For the months of February through to August there were seven months, each of 30 days.
Rule 251 makes the distinction between different types of bond and bonds that were issued before and after the introduction of the single European currency in January 1999. The “number of days accrued” and the “number of days in the year” conventions described in Rule 251 can be found in
Table 2.18
and are summarised in
Figure 2.1
.
TABLE 2.18
ICMA rule on accrued interest conventions
| Bond Type | When Issued | Number of Days Accrued | Number of Days in a Year |
| All convertible bonds | Before 01 Jan 1999 | 360-days-per-year basis (a month is 30 days) | 360 days |
| All straight bonds | Before 01 Jan 1999 | 360-days-per-year basis (a month is 30 days) | 360 days |
| Euro sterling FRNs | Any time | Calendar days (incl. leap year) | Actual number of days in the calendar year |
| All FRNs (except Euro sterling FRNs) | Any time | Calendar days (incl. leap year) | 360 days |
| Non-USD-denominated convertible bonds | After 31 Dec 1998 | Calendar days (incl. leap year) | Actual calendar days in coupon period multiplied by number of coupon periods in the year |
| Non-USD-denominated straight bonds | After 31 Dec 1998 | Calendar days (incl. leap year) | Actual calendar days in coupon period multiplied by number of coupon periods in the year |
| USD-denominated convertible bonds | After 31 Dec 1998 | 360-days-per-year basis (a month is 30 days) | 360 days |
| USD-denominated straight bonds | After 31 Dec 1998 | 360-days-per-year basis (a month is 30 days) | 360 days |
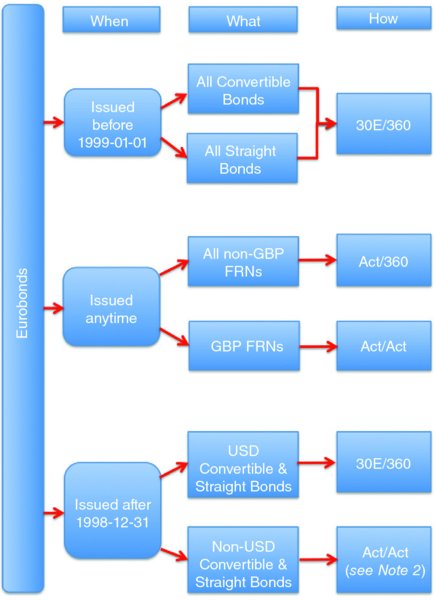
FIGURE 2.1
Summary of ICMA accrued interest rules
Note 1: Day basis (the “How” in
Figure 2.1
) is explained in
Table 2.19
.
TABLE 2.19
Day basis
| Convention | Explanation |
| 30E/360 | 30 days in a month, 360 days in a year, using the European method for dates falling on the 31st of a month (European 30/360). |
| Actual/360 | Actual calendar days in each month, 360 days in a year. |
| Actual/Actual | Actual calendar days in each month, actual days in each year (both including the extra day in leap years). |
| Other variations include: | |
| Actual/365 | Actual calendar days in each month, 365 days in a year. |
| 30/360 | 30 days in a month, 360 days in a year, using the NASD method for dates falling on the 31st of a month. |
Note 2: The full text of “/Actual” is: “⦠actual calendar days in the coupon period multiplied by the number of coupon periods in the year”. So, for example, if the coupon period contains 181 days and the bond is a semi-annual coupon payer, then the divisor is 362 days.
Note 3: “Actual” includes the extra day in a leap year.
Day/year conventions also differ when we consider government bonds and domestic corporate bonds.
- Actual/Actual:
Applicable to most government bonds and many corporate bonds. - 30/360:
Used by many corporate bonds. Assumes 30 days for each month, even for those months that have 28, 29 or 31 days. - 30E/360:
A slight modification of the 30/360 convention common in the Eurobond market. If either the previous coupon date or the settlement date falls on the 31st of any month, it is assumed to be the 30th. - Actual/360:
Used by some supranational and corporate bonds. - Actual/365:
Used by some supranational and corporate bonds.