Fortune's Formula (23 page)

D
ANIEL
B
ERNOULLI
came from an insanely competitive family of eighteenth-century geniuses. It was Daniel’s uncle Jakob who had discovered the law of large numbers. Jakob tutored his brother Johann in math. Johann was as smart as Jakob was; he was also a braggart. The Bernoulli brothers acquired the unfortunate habit of working on the same problems competitively. They brutally attacked each other in print.

Johann grew into an embittered man who took out his frustrations on his son Daniel (1700–1782). Daniel was both a mathematician and a physicist. He published a famous analysis of the casino game of faro and discovered the “Bernoulli effect” later used in the design of aircraft wings. Johann took little visible joy in his son’s triumphs. When father and son were jointly awarded a French Academy of Sciences prize in 1734, Johann threw Daniel out of the house. Johann grumbled that he alone should have won the award. In 1738 Daniel published an important book called
Hydraulica
. The following year, his father published nearly the same book under his own name, with the false date of 1732. This ruse allowed Johann to claim that his son’s book was a plagiarism.

It must have been with some relief that Daniel left his father for far-distant St. Petersburg. There, working for the Westernizing Russian court, Daniel wrote an article that was to be influential for the reception of Claude Shannon and John Kelly’s ideas among twentieth-century economists. The article concerned a fictitious wager devised by still another gifted Bernoulli, Nicolas, a doctor of law at the University of Basel. Nicolas was Daniel’s cousin. The wager involves a game of doubling that may recall Kelly’s quiz-show inspiration,
The $64,000 Question
. As Daniel described it in 1738,

How much can Paul expect to win, on the average? To find the mathematical expectation of a random event, you multiply its probability by its value. There’s a ½ chance of heads on the first throw, and heads wins Paul 1 ducat (worth about $40 today). Multiplying ½ times 1 ducat gives an expected value of ½ ducat.

That is just for the case in which the first toss is heads. There are many other ways to win. Should the first throw come up tails, Peter tosses again. If the
second
throw is heads, Paul wins 2 ducats. The chance of winning 2 ducats is ¼, since that requires that the first throw be tails (½ chance)
and
that the second throw be heads (½ chance). A ¼ shot at 2 ducats is worth ½ ducat.

Likewise, there’s a 1/8 chance of winning 4 ducats, which is worth ½ ducat itself. There’s a 1/16 chance of 8 ducats, a 1/32 chance of 16 ducats…All of these distinct scenarios each have an expectation of ½ ducat. Paul’s total expected winnings should therefore be the sum of an infinite series of ½-ducat terms. His expected winnings are infinite.

Will you get infinitely rich by playing this game? No. If you don’t believe it, try flipping a coin. See how much you would have won.

The infinite expectation is a big problem for anyone who wants to use math to decide what to do in the real world. It implies that no amount of money is too much to pay for the privilege of playing this game. Were a casino to charge a million dollars to play this game, rational customers should jump at the chance, it would seem. Same if the casino charged a trillion dollars.

You might prefer to think of the wager as an initial public offering of a growth stock. People evaluating a new company’s prospects must conclude that there are many scenarios with varying degrees of probability and profitability. Somehow they mentally tally up the outcomes to arrive at a reasonable price to pay for the stock. Bernoulli’s example suggests that in some situations conventional reasoning could find a stock worth buying at any price, no matter how high.

Both Nicolas and Daniel Bernoulli knew this was absurd. Daniel wrote,

Daniel published these words in Latin. The wager has come to be known as the “St. Petersburg wager” or “St. Petersburg paradox.” It has provoked sporadic interest ever since. A mention in John Maynard Keynes’s 1921
Treatise on Probability
made it part of the mental furniture of nearly every twentieth-century economist. Bernoulli’s wager makes an appearance in von Neumann and Morgenstern’s
Theory of Games and Economic Behavior
and in papers by Kenneth Arrow, Milton Friedman, and Paul Samuelson.

The paradox can be resolved easily by noting that Peter would have to possess infinite wealth to make good on the game’s potential payouts. No one has infinite wealth. Therefore most of the terms of the infinite series are irrelevant. A minuscule chance of winning a quadrillion dollars is not worth what you might compute. It’s worth practically
nothing
because no one has a quadrillion dollars to award.

Suppose a casino offered this wager with winnings capped at a billion dollars. How much would the wager be worth then? A lot less! Assume prizes start with a dollar. Normally, the prize for heads on the 31st toss would be $1,073,741,824. The most reasonable course for the casino would be to halt the game at 30 tosses and award the billion dollars to anyone who has gotten 30 tails. The expected value of this truncated game is a measly $15.93.

That’s a lot more reasonable. The wager is not worth infinity, just a few dollars. This explanation of the puzzle is as good as any hardheaded realist could ask for. Yet philosophers, mathematicians—even economists—have rarely accepted this solution. Most take the position that we can pretend that Peter possesses infinite wealth. Isn’t it still ridiculous to say that Paul should be willing to pay any amount to play the game?

Daniel Bernoulli thought so. He proposed a different solution that was highly influential for future economic thought. Bernoulli drew a distinction between money and the value people place on money. To a billionaire, $1,000 is pocket change. To a starving beggar, $1,000 may be a fortune. The value of a financial gain (or loss) depends on the wealth of the person it affects.

You’re probably saying to yourself that you already knew that. Well okay, Bernoulli’s real contribution was to coin a word. The word has been translated into English as “utility.” It describes this subjective value people place on money. Bernoulli claimed that people instinctively act to achieve the greatest possible utility—not necessarily the greatest number of dollars or ducats. “The
value
of an item must not be based on its
price
,” Bernoulli wrote, “but rather on the
utility
it yields. The price of the item is dependent only on the thing itself and is the same for everyone; the utility, however, is dependent on the particular circumstances of the person making the estimate.”

How much less is a dollar worth to a rich person than a poor one? The only honest answer is, “It depends.” As an example, Bernoulli sketched the case of a rich man who is imprisoned and needs exactly 2,000 ducats
more than he has
in order to buy his freedom. This man might place a greater valuation on those needed 2,000 ducats than a poorer man with no such pressing need.

This is a contrived predicament. Most of the time, a rich person would value a 2,000-ducat gain less than a poorer person would. Bernoulli offered a rule of thumb. “In the absence of the unusual,” he wrote, “the utility resulting from any small increase in wealth will be inversely proportionate to the quantity of goods previously possessed.”

In other words, your friend who is
twice
as rich as you would be only
half
as delighted to win a $100 bet as you would be. Picking up the dinner bill hurts him only half as much.

You can make a chart of utility vs. wealth. If people’s valuation of money were in direct proportion to their wealth, the chart would be a straight line. With Bernoulli’s rule of thumb, the line curves. This reflects the fact that it takes a large dollar gain to make the same difference to a rich person as a smaller dollar gain would to a poor person. The shape of this curve (and Bernoulli’s rule about the value of a monetary gain being inversely proportional to wealth already possessed) describes a logarithmic function. Bernoulli’s rule of thumb is therefore called logarithmic utility.

Bernoulli used utility to resolve the St. Petersburg paradox. Assume that Paul values gains in inverse proportion to his wealth. That means that the value Paul places on a 2-ducat win is not quite twice that of a 1-ducat gain. Your second ducat, like your second million, is never quite as sweet.

Logarithmic Utility

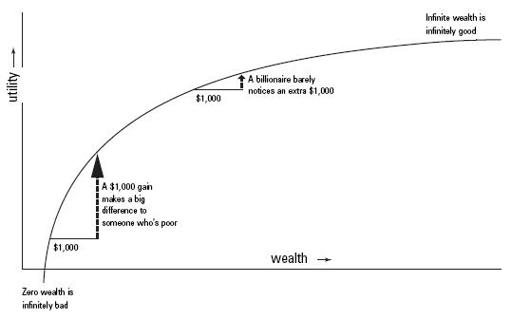
This means that the terms in the infinite series need to be adjusted downward to account for the diminishing returns of large winnings. Though the series is still infinite, it becomes one of those well-mannered infinite series that converges. You can add up ½ + ¼ + 1/8 + 1/16…and never quite reach 1, no matter that the series is endless. When Bernoulli’s series of expectations is adjusted this way, it too converges to a finite and modest sum.

Economic thinkers were infatuated with logarithmic utility for the next couple of centuries. British economist William Stanley Jevons (1835–1882) maintained that logarithmic utility applied to consumer goods as well as wealth: “As the quantity of any commodity, for instance, plain food, which a man has to consume, increases, so the utility or benefit derived from the last portion used decreases in degree.” You might say this explains how all-you-can-eat restaurants stay in business. In 1954 Leonard Savage called the logarithmic curve a “prototype for Everyman’s utility function”—a reasonable approximation to how most people value money, most of the time, over the range of dollar values they normally encounter.

Not everyone agreed. By Savage’s time, logarithmic utility had taken on a fusty, old-fashioned cast. One blow to the concept was the realization that logarithmic utility is not an entirely satisfying resolution to the St. Petersburg paradox. In the 1930s, Vienna mathematician Karl Menger pointed out that it is easy to come back with revised versions of the St. Petersburg wager where Bernoulli’s solution fails. All you have to do is to sweeten the payoffs. Instead of offering 1, 2, 4, 8 ducats on successive throws, offer something like 2, 4, 16, 256 ducats…You can arrange to have the prizes escalate so fast that the expected utility is again infinite.

Menger’s most devilish counterexample was to have the wager’s prizes not in dollars or ducats but
utiles
. A utile is a hypothetical unit of utility. You would win 1, 2, 4, 8…utiles, depending on how many tosses it takes. The value of the wager, now in expected utility, is infinite. A rational person would supposedly give up anything he’s got to play this game—which is still absurd because he’s likely to win the utile equivalent of chump change.

What should we make of all this? Perhaps not much. Paul Samuelson believed that the supercharged versions of the St. Petersburg paradox do not “hold any terrors for the economist.” The nub of the issue is that Bernoulli’s utility function is psychologically unrealistic at the extremes of wealth.

A better resolution invokes a “bliss level.” This is a supposed ceiling on utility. Figure how much money you would need to satisfy every need or desire that can possibly be satisfied with mere material things. That amount of money, and the corresponding utility, is the bliss level.

An upper limit to utility works much like an upper limit to the dollars a casino is able to pay out. It truncates the infinite series at a reasonable and finite value.

A logarithmic utility function has no bliss level. The curve in the chart appears to flatten out toward the upper right. It never ceases rising, however. This means, for instance, that someone with logarithmic utility would be equally delighted by any gain that increased total wealth by a factor of ten. Increasing your net worth from $10,000 to $100,000 would be just as welcome as going from $100,000 to $1 million, or from $1 million to $10 million.