Fortune's Formula (25 page)

T
ELLING INVESTORS
to maximize the geometric mean may cause a double take. The geometric mean of return is none other than the “compound return on investment” that is Wall Street’s usual scorecard. Everyone has been talking in that prose all along.

Latané’s University of North Carolina colleague Richard W. McEnally observed that “the idea that we should pick the investment which will maximize the rate of growth of a portfolio may sound…like much advice from economists—laudable, but difficult or impossible to implement in practice because of the knowledge of the distant future it would require.”

A few examples will show how the geometric mean principle works. Simple case: You’ve got just two choices for your money, a savings account paying 3 percent interest, and another savings account paying 4 percent. Both accounts are guaranteed by the FDIC. Because there’s no risk, the arithmetic and geometric mean returns are the same for each account. Both Kelly
and
Markowitz say to put your money in the 4 percent account.

The choice is not so pat when there’s an element of chance. A hot technology stock might have a higher arithmetic mean return than a boring blue chip, but it is also likely to have a higher volatility, which could result in a lower geometric mean. Are you better off buying the technology stock or not?

This is the sort of question that the Kelly criterion can
potentially
answer. I say “potentially” because no one really knows the probabilities underlying stock investments.

That doesn’t prevent analysts from cooking up target figures and mathematical models. A mathematical model attempts to reduce an imperfectly known real-world situation to a game of chance.

Imagine, then, that you are thinking of investing in three penny stocks. You do a lot of research and devise a mathematical model of the stocks’ returns after a year. In principle, you could build a wheel of fortune with the same probability distribution as the stock. Divide the rim of the wheel into however many spaces you need. Mark the spaces with numbers telling how much a dollar invested in the stock could be worth after a year. If your model’s any good, playing the wheel of fortune is about the same as investing in the stock.

Let’s say you build a wheel of fortune for each of three penny stocks and they look like this:

Kelly vs. Markowitz Criterion

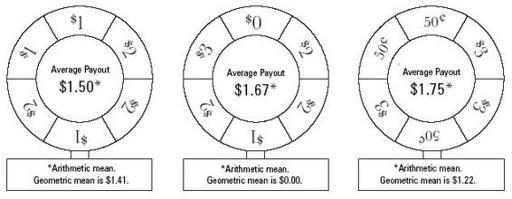
These wheels are simpler than anyone’s rational idea of a stock’s prospects. But you get the idea. By adding enough spaces on the wheel, you could represent any precise idea you have about the stock’s returns and their probabilities.

Suppose you had to put all your money on just one wheel. Which is best? It’s tough to tell. That’s why it’s useful to compute “average” returns. As sometimes happens, the arithmetic mean return, being bigger, gets top billing, while the geometric mean is buried in the fine print.

The third wheel has the highest arithmetic mean. The first wheel has the highest geometric mean. Assuming these are the only three choices and you have to pick one, the Kelly criterion would have you put your money on the first wheel.

The
worst
wheel, by the Kelly philosophy, is the second. That’s because it has a zero as one of its outcomes. With each spin, you risk losing everything. Any long-term “investor” who keeps letting money ride on the second wheel must eventually go bust. The second wheel’s geometric mean is
zero
.

What does mean-variance analysis say? To answer that, you have to compute the variance of the wheels’ returns. I’ll spare you the trouble—the variance of the wheels increases from left to right. So does the arithmetic mean return. Consequently, Markowitz theory refuses to decide among these three wheels. All are legitimate choices. A risk-tolerant investor looking for the highest return might choose the third wheel. A conservative investor willing to sacrifice return for security might choose the first. The middle wheel is good, too, for people in the middle.

The last bit of advice is particularly hard to swallow. Most would agree that the middle wheel is the riskiest because it alone poses the danger of total loss. Yet the middle wheel has a lower variance than the third because its outcomes are less dispersed. This is one example of how variance is not a perfect measure of risk.

One point where the Markowitz and Kelly approaches concur is the value of diversification. A racetrack gambler who “diversifies” by betting on every horse achieves a higher geometric mean than someone who bets everything on a single horse (and risks losing it all). The same goes for someone who diversifies by buying many stocks.

There are two ways for a speculator to put the law of large numbers to work. John Kelly mentioned both in his article. In an unintended take on twentieth-century gender issues, he described a gambler whose wife permits him to place a $1 bet each week. He is not allowed to reinvest any past weeks’ winnings.

This gambler should forget about the Kelly criterion. He’s better off choosing the gamble with the highest arithmetic mean. The reason is that the henpecked gambler’s winnings do not compound; they simply accumulate.

This gambler does best by choosing the third wheel above, with the highest arithmetic mean ($1.75). After a year of wagering, the law of large numbers implies that the gambler’s actual winnings per week will be proportionately close to the expectation. The gambler will have about 52 times $1.75 or $91 at year’s end (representing a profit of about $39 when you subtract the total of $52 he wagered).

Had the dollar-a-week gambler chosen the first wheel, he would have about $78 (a $26 profit), and with the second, he would likely have around $87 ($35 profit).

The Kelly criterion is meaningful only when gambling profits are reinvested. Take a gambler who starts with a single dollar and rein-vests his winnings once a week. (He does not add any more money, nor take any out.) Should this gambler bet on the first wheel, he can expect to increase his wealth by a factor of 1.41 each week. After 52 weeks, his fortune would be something like

$1.41
⁵²
= $67,108,864

The Kelly bettor would have run a single dollar into millions. Compare this to the other two wheels. A compounding bettor who bets on the second wheel can expect after a year to have

$0
⁵²
= $0

Zip! This gambler is almost certain to get a zero in a year’s worth of betting. Once that happens, he’s broke.

The estimate for the third wheel is

$1.22
⁵²
= $37,877

None of these figures are “guaranteed.” The law of larger numbers doesn’t work that way. A few more or less lucky spins, and the results could be much different. That said, it is close to certain that the first wheel will yield vastly more than the third, and anyone so foolish as to make parlaying bets on the second will be broke.

Standard mean-variance analysis does not treat the compounding of investments. It is, you might say, a theory for Kelly’s dollar-a-week gambler. But as the wealth to be amassed by compounding is so fantastically greater than can be achieved otherwise, a practical theory of investment must largely be a theory of
re
investment.

When you try to apply Markowitz theory to compounding, the results can be absurd. One of Ed Thorp’s theoretical contributions to the Kelly criterion literature is a 1969 paper in which he demonstrated the partial incompatibility of mean-variance analysis and the policy of maximizing the geometric mean. Thorp closes his article by declaring that “the Kelly criterion should replace the Markowitz criterion as the guide to portfolio selection.”

Perhaps no economist of the time would have dared such a heresy. It seems unlikely a major economic journal would have published such talk. Thorp’s article appeared in the
Review of the International Statistical Institute
. Probably few economists saw it. In any event, few economists had heard of John Kelly. That was about to change.

I
N A WAY,
Claude Shannon was the efficient market mob’s worst nightmare. He was a smart guy making money hand over fist in the market. He had turned his formidable genius to the problem of arbitrage. In the mid-1960s, Shannon began holding regular meetings at MIT on the subject of scientific investing. These were attended by an eclectic assortment of people, including Paul Samuelson.

Shannon gave a couple of talks on investing at MIT, circa 1966 and 1971. By then the broad MIT community had heard stories of Shannon’s stock market acumen. So many people wanted to attend one talk that it had to be moved to one of MIT’s biggest halls.

Shannon’s main subject was an incredible scheme for making money off the
fluctuations
in stocks. You can make money off stocks when they go up (buy low, sell high). You can make money when they go down (sell short). You just have to know
which
way prices are going to move. That, suggested Bachelier, Kendall, and Fama, is impossible.

Shannon described a way to make money off a random walk. He asked the audience to consider a stock whose price jitters up and down randomly, with no overall upward or downward trend. Put half your capital into the stock and half into a “cash” account. Each day, the price of the stock changes. At noon each day, you “rebalance” the portfolio. That means you figure out what the whole portfolio (stock plus cash account) is presently worth, then shift assets from stock to cash account or vice versa in order to recover the original 50–50 proportions of stock and cash.

To make this clear: Imagine you start with $1,000, $500 in stock and $500 in cash. Suppose the stock halves in price the first day. (It’s a really volatile stock.) This gives you a $750 portfolio with $250 in stock and $500 in cash. That is now lopsided in favor of cash. You rebalance by withdrawing $125 from the cash account to buy stock. This leaves you with a newly balanced mix of $375 in stock and $375 cash.

Now repeat. The next day, let’s say the stock
doubles
in price. The $375 in stock jumps to $750. With the $375 in the cash account, you have $1,125. This time you sell some stock, ending up with $562.50 each in stock and cash.

Look at what Shannon’s scheme has achieved so far. After a dramatic plunge, the stock’s price is back to where it began. A buy-and-hold investor would have no profit at all. Shannon’s investor has made $125.

This scheme defies most investors’ instincts. Most people are happy to leave their money in a stock that goes up. Should the stock keep going up, they might put more of their free cash into the stock. In Shannon’s system, when a stock goes up, you sell some of it. You also keep pumping money into a stock that goes down—“throwing good money after bad.”

Look at the results. The lower line of the chart shows the price of an imaginary stock that starts at $1 and either doubles or halves in price each time unit with equal probability. This is a geometric random walk, a popular model of stock price movements. The basic trend here is neither up nor down. The lower line therefore represents the wealth of a buy-and-hold investor who has put all her money in the stock (assuming no dividends).

Shannon’s Demon

The chart’s upper line shows the value of a 50–50 stock and cash portfolio that is rebalanced each time unit. This line trends upward. The dollar scale on this chart is logarithmic, so the straight trend line actually means exponentially growing wealth.

The rebalanced portfolio is also less
volatile
than the stock. The scale of the jitters is relatively less for the rebalanced portfolio than for the stock itself. Shannon’s rebalancer is not only achieving a superior return, but a superior risk-adjusted return.

How does Shannon’s stock system work?
Does
it work?

Shannon’s system bears a telling similarity to a great puzzle of physics. In his 1871 book
Theory of Heat
, British physicist James Clerk Maxwell semiseriously described a perpetual motion machine. The machine could be as simple as a container of air divided into two chambers by a partition. There is a tiny trapdoor in the partition. To operate the machine, you need, as Maxwell put it, a “being whose facilities are so sharpened that he can follow every molecule in its course.”

“Maxwell’s demon,” as this being was called, uses his superpower vision and reflexes to sort air molecules by their speed. When a fast molecule approaches the trapdoor from the right, the demon opens the trapdoor and lets the molecule pass into the left side. When a slow molecule approaches from the right, the demon shuts the trapdoor to keep it in the right side.

After much sorting, the demon will have most of the fast molecules on the left side, and the slow molecules on the right side. This is significant because temperature is the measure of how fast molecules are moving, on the average. The demon has created one chamber of hot gas and another of cold gas, all without expending any real energy. (Oh, the demon has to keep opening and shutting the door. But if the door is very light and very rigid, the energy requirement can be as small as you like.)

A steam engine generates energy from a temperature difference. By hooking up a steam engine to his hot and cold gas, the demon can therefore produce usable energy out of the random motions of molecules.

Few physicists imagined that such a device was possible. It was too well established that you cannot conjure up energy out of thin air. Nor can you reduce the disorder (entropy) of the universe, which the demon is also doing. The puzzle was deciding
why
it was impossible.

There is of course no such thing as a demon who can see individual molecules. You can imagine a nano-scale valve or robot that does what the demon was supposed to do. Many twentieth-century physicists and scientifically minded philosophers did just that in trying to resolve the puzzle. They mostly got sidetracked on nuts-and-bolts issues of how a tiny mechanism could detect molecules and open or close an atomic-scaled door. Because quantum theory was new and exciting, most of their thinking invoked the famous principle that you can’t observe anything without changing it. In order to
see
the molecules, the demon must shoot photons (particles of light) at them. The photons scatter the molecules, making his observations unreliable. The uncertainty principle defeats the demon—or so it was argued.

Actually, quantum theory is largely a red herring here. Physicists Leo Szilard, Léon Brillouin, and Denis Gabor attempted to resolve the problem in terms of what we would now call information. Szilard, writing in 1929, described something very close to the bit, anticipating Shannon. A full solution was impossible without the insights of Shannon’s theory. It was supplied in 1982 by IBM scientist Charles Bennett.

It is helpful to reimagine Maxwell’s situation so that the demon has ESP, or a “private wire,” telling him when to open and shut the trapdoor. (He does not have to dirty his hands with quantum physics.) The simplified demon simply receives a stream of bits on his pager. When he receives a “1” he opens the trapdoor; when he gets a “0” he closes it. All this information is magically correct.

The more bits received, the more molecules the demon can sort, and the more energy he can produce. This much recalls Kelly’s gambler, who converts a stream of bits into capital growth. Now ask yourself: Is Kelly’s gambler getting “something for nothing”? Well, yes, if you look at his bankroll and nothing else. No, if you look at the big picture. It is other people’s money he’s winning.

Much the same applies to Maxwell’s demon. Focus just on the air molecules, and the demon’s sorting decreases entropy and creates energy from nothing. Look at the big picture and you will discover that the demon is only redistributing these quantities.

Charles Bennett argued that the demon is necessarily increasing the entropy of his own brain. In Maxwell’s time, no one thought about the demon having a brain. The very word “demon” emphasized that it was fiction. Shannon’s theory presented information as an integral part of the physical world. Any demon—whether made of flesh and blood, microchips, or nanovalves—needs a physical “brain” to operate.

The demon does not need
much
of a brain. He is little more than a remote-control garage door opener. An incoming stream of bits tells him what to do and he does it. But at the very least, the demon’s brain must be capable of existing in one of two states. There must be one state where he opens the trapdoor, and another where he closes it. The demon needs (at least) one bit of memory.

In 1961 Rolf Landauer, another IBM scientist, showed that erasing computer memory always increases entropy. You can get the flavor of his demonstration from this: Suppose you’ve got an MP3 file of a garage band’s unreleased song. It’s the only copy in the world. If you erase that file, it will never be possible to recover exactly that particular performance. To erase is to destroy a small part of history. Erasing increases uncertainty about the past state of the world. Uncertainty is entropy.

In his mathematical analysis, Landauer showed that erasing digital memory must increase entropy as measured by physicists. Notice that Maxwell’s demon will have to do a
lot
of erasing. Every time a new bit comes in on his private wire, he must “erase” the old bit, with a consequent increase in entropy. Charles Bennett used Landauer’s result to argue that the entropy increase in the demon’s brain must be at least as great as the entropy decrease in the chamber of air.

The bottom line is that the demon can’t make a net energy profit after all. It will take at least as much energy to run his brain as he can produce by sorting. Maxwell’s demon is only redistributing entropy and energy.

In 1974 Paul Samuelson wrote that a high-PQ trader “is in effect possessed of a ‘Maxwell’s Demon’ who tells him how to make capital gains from his effective peek into tomorrow’s financial page reports.” Like Maxwell’s demon, Shannon’s stock system turns randomness into profit. Shannon’s “demon” partitions his wealth into two assets. As the asset allocation crosses the 50 percent line from either direction, the demon makes a trade, securing an atom-sized profit or making an atom-sized purchase—and it all adds up in the long run.

The “trick” behind this is simple. The arithmetic mean return is always higher than the geometric mean. Therefore, a volatile stock with zero geometric mean return (as assumed here) must have a
positive
arithmetic mean return.

Who can make money off an arithmetic mean? One answer: Kelly’s dollar-a-week gambler. One week he buys $1 worth of penny stock. If he’s lucky, the stock doubles. He sells, locking in a dollar profit. (It promptly goes into his wife’s hat fund.)

The next week he gets a brand-new dollar and buys more penny stock. This time, he’s unlucky. The stock loses half its value. He sells, having lost 50 cents.

Mr. Dollar-a-Week has gained a dollar and lost 50 cents in this typical scenario. He has averaged a 25 percent weekly profit while the stock’s price has gone nowhere.

The problem with Mr. Dollar-a-Week is that he doesn’t think
big
. Because he bets the same amount each week, his expectation of profit remains the same.

Someone serious about making money should follow the (regular) Kelly gambler, who always maximizes the geometric mean. When the Kelly gambler is allowed to split his bankroll between the cash account and the random-walk stock in any proportion, he will choose a 50–50 split, for this has the highest geometric mean. Shannon’s scheme is a special case of Kelly gambling.

Kelly’s gambler does not coin money. He only redistributes it. Here the parallel breaks down. Maxwell’s demon will disappoint anyone looking for an environmentally friendly energy source. The redistributive nature of Kelly gambling rarely bothers people. Racetracks and stock markets are full of people who are only too glad to redistribute money into their own pockets.

There was a question-and-answer period after Shannon’s talk. The very first question posed to Shannon was, did he use this system for his own investments?

“Naw,” said Shannon. “The commissions would kill you.”

Shannon’s stock scheme harvests volatility.
If
you could find a stock that doubles or halves every day, you’d be in business. As described above, $1 can be run into a million in about 240 trades. The commissions would be thousands of dollars. So what? You’d end up with a million for every dollar invested…

No stock is anywhere near that volatile. With realistic volatility, gains would come much slower and would be less than commissions.

There are other problems. The Shannon system postulates a stock whose geometric mean return is
zero
. It plays off a common frustration with stocks, which all too often seem to “go nowhere.” Efficient market theorists say no stock has zero mean return. Who would buy such a stock? In the realistic case of a stock that tends to drift upward, the optimal allocation of assets between stock and cash will differ. When the stock has a high enough mean return, the Kelly-optimal trader will commit all his assets to the stock. The rebalancing is then moot.