Read Games and Mathematics Online
Authors: David Wells
Games and Mathematics (28 page)
Figure 14.4
Basic cycloid figure
Basic cycloid figure

The
cycloid has so many beautiful features and was the cause of so much acrimonious controversy in the seventeenth century that is was called the Helen of Geometry. Among other properties, it is the curve of quickest descent, or brachistochrone: the fastest path for a ball to move from A to a lower point B under gravity is part of a cycloid; and the tautochrone: a ball in a cycloidal basin has the same period of oscillation wherever it starts.
cycloid has so many beautiful features and was the cause of so much acrimonious controversy in the seventeenth century that is was called the Helen of Geometry. Among other properties, it is the curve of quickest descent, or brachistochrone: the fastest path for a ball to move from A to a lower point B under gravity is part of a cycloid; and the tautochrone: a ball in a cycloidal basin has the same period of oscillation wherever it starts.
Galileo
named it the cycloid in 1599 and tried to find its area by cutting a cycloid out of metal sheet and weighing it. This suggested that the area was 3π
r
2
where
r
is the radius of the generating circle, but Galileo was not convinced by his own experiment.
named it the cycloid in 1599 and tried to find its area by cutting a cycloid out of metal sheet and weighing it. This suggested that the area was 3π
r
2
where
r
is the radius of the generating circle, but Galileo was not convinced by his own experiment.
Later Toricelli (1608–1647), the inventor of the barometer, and Fermat and Descartes and others all found the area to be indeed 3π
r
2
. The following simple proof is a cross between those of Roberval (1602–1675) and Pascal [Boyer
1956
: 135–6; Coolidge
1949
: 100].
r
2
. The following simple proof is a cross between those of Roberval (1602–1675) and Pascal [Boyer
1956
: 135–6; Coolidge
1949
: 100].
Figure 14.5a
Cycloid with three circles
Cycloid with three circles

Figure 14.5
a shows that when the circle has rolled to touch the line PU at Q, (which happens to be one quarter of the way from P to U in our figure), the point P has risen to Pʹ. If the original circle had simply rotated about its centre without rolling anywhere, then P would have risen to R. Since, however, it has
also moved a distance PQ to the right, we can actually construct the point Pʹ by using the fact that RPʹ = PQ. We also need to notice that the arc RP = arc PʹQ = arc VU.
a shows that when the circle has rolled to touch the line PU at Q, (which happens to be one quarter of the way from P to U in our figure), the point P has risen to Pʹ. If the original circle had simply rotated about its centre without rolling anywhere, then P would have risen to R. Since, however, it has
also moved a distance PQ to the right, we can actually construct the point Pʹ by using the fact that RPʹ = PQ. We also need to notice that the arc RP = arc PʹQ = arc VU.
Next, looking at the distance the circle still has to roll, we see that PʹV = QU and that both of these lengths is equal to arc VW.
Figure 14.5b
Cycloid divided
Cycloid divided

The area of the half-cycloid is the sum of all the strips PʹVVʹ which we can think of as,
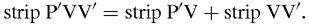 The strips VVʹ, in the limit, will be the area of the half-circle, or
The strips VVʹ, in the limit, will be the area of the half-circle, or
 π
π
r
2
, but what is the limit of the sum of the strips PʹV? To find it we draw the graph of the arc lengths VW against
y
, starting with
y
= 2
r
when
s
= 0 and moving to
y
= 0 when
s
= π
r
(
Figure 14.6
).
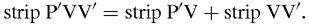
 π
πr
2
, but what is the limit of the sum of the strips PʹV? To find it we draw the graph of the arc lengths VW against
y
, starting with
y
= 2
r
when
s
= 0 and moving to
y
= 0 when
s
= π
r
(
Figure 14.6
).
Figure 14.6
Cycloid with graph of
y
against
s
Cycloid with graph of
y
against
s

We don't know, and we don't need to know, what
s
is as a function of
y
. Roberval in his proof just called the matching curve, the ‘companion of the cycloid’. It is in fact just what it looks like, a sine curve. What we do need to notice is that since the half-circle is symmetrical about the line
y
=
r
, the rate at which
s
increases will be the same at points symmetrical about the centre line,
y
=
r
, and so the curve will have point symmetry about its centre, C, where
y
and
s
momentarily increase together, making the gradient of the tangent 45°.
s
is as a function of
y
. Roberval in his proof just called the matching curve, the ‘companion of the cycloid’. It is in fact just what it looks like, a sine curve. What we do need to notice is that since the half-circle is symmetrical about the line
y
=
r
, the rate at which
s
increases will be the same at points symmetrical about the centre line,
y
=
r
, and so the curve will have point symmetry about its centre, C, where
y
and
s
momentarily increase together, making the gradient of the tangent 45°.
We conclude that the area under the curve which is the limit of the second sum, is half the area of the rectangle, or
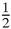 × 2
× 2
r
× π
r
= π
r
2
. Adding the area of the half-circle we get the area of 3π
r
2
/2 for the half cycloid, and 3π
r
2
for the whole cycloid.
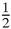 × 2
× 2r
× π
r
= π
r
2
. Adding the area of the half-circle we get the area of 3π
r
2
/2 for the half cycloid, and 3π
r
2
for the whole cycloid.
This dynamic way of thinking about the ball actually rolling along the line and then ‘unwrapping’ the perimeter of the half-circle to create the side of a rectangle, is typical of the way of thinking of many seventeenth-century mathematicians. It had to be highly creative and imaginative – like a brilliancy at chess – because no general methods of finding areas were known. The division of the area into parallel strips was itself a very general idea, but its application was delightfully different in every particular case.
Although Descartes (and Fermat) had created coordinate geometry, and although Apollonius (292–190 BC) had long ago proved a property of the parabola which was equivalent to the equation
ay
=
x
2
, mathematicians still tended to think of curves as created dynamically by movement, rather than being defined statically by equations [Boyer
1956
: 134–5].
ay
=
x
2
, mathematicians still tended to think of curves as created dynamically by movement, rather than being defined statically by equations [Boyer
1956
: 134–5].
As it happens, the cycloid cannot be simply defined by an equation of the form
y
=
f
(
x
), but only by parametric equations:
x
=
r
(
t
− sin(
t
)) and
y
=
r
(1 – cos(
t
)). Today, its area can be found by basic calculus. It is not especially simple but it is not complicated either, requires no imagination or insight and is indeed completely routine, a matter of applying well-known and well-understood techniques.
y
=
f
(
x
), but only by parametric equations:
x
=
r
(
t
− sin(
t
)) and
y
=
r
(1 – cos(
t
)). Today, its area can be found by basic calculus. It is not especially simple but it is not complicated either, requires no imagination or insight and is indeed completely routine, a matter of applying well-known and well-understood techniques.
The tangent at any point on the cycloid can also be found today by pure technique, but Descartes had no difficulty in finding it by a dynamic argument which we can still appreciate, not least because it is so simple and elegant.
In
Figure 14.7
is half a cycloid as before, and a point Pʹ on the cycloid. The first puzzle is to find the position of the rolling circle PT when P has moved to Pʹ. To solve this, Descartes drew PʹV parallel to PU and then found Q on PU so that QU = PʹV, exploiting the property that we noted earlier. Q is where the rolling circle touches PU and is also what we today would call the
instantaneous centre of rotation
of the line QPʹ at that moment. We at once conclude that the tangent is perpendicular to QPʹ, as drawn.
Figure 14.7
is half a cycloid as before, and a point Pʹ on the cycloid. The first puzzle is to find the position of the rolling circle PT when P has moved to Pʹ. To solve this, Descartes drew PʹV parallel to PU and then found Q on PU so that QU = PʹV, exploiting the property that we noted earlier. Q is where the rolling circle touches PU and is also what we today would call the
instantaneous centre of rotation
of the line QPʹ at that moment. We at once conclude that the tangent is perpendicular to QPʹ, as drawn.
Figure 14.7
Descartes: tangent to cycloid
Descartes: tangent to cycloid

Other books
Sunset Hearts by Macy Largo
Sex and the Citadel by Shereen El Feki
Inner Tube: A Novel by Hob Broun
Falling Fast by Lucy Kevin
The Shifter's Conspiracy (Paranormal BBW Werewolf Romance Novella) by Laurent, Cassie
The Alejandra Variations by Paul Cook
So Sad Today by Melissa Broder
The Alternative Detective (Hob Draconian) by Robert Sheckley
the imprecation of wizards by Shahram Azad
