How to Pass Numerical Reasoning (23 page)

So Jamie’s average speed for the whole distance is 8 mph.

Summary of rates formulae

Distance
= Rate × Time

Rates practice questions

Set a stopwatch and aim to complete each question within 80 seconds.

Q1
Yousuf sets off on the annual London to Cambridge bike ride. He cycles at a steady pace of 9 miles an hour and crosses the finishing line 6 hours later. What is the distance of the London to Cambridge ride?

Q2
Jo walks along the South Downs Way at a rate of 4.5 miles per hour. After walking for 3½ hours, she still has 6 miles left to walk. What is the total distance she intends to walk?

Q3
A singer is on stage with a bass guitarist. Part of the dance routine requires them to move to opposite ends of the stage for one section of the song. Standing together, they start to move away from each other. The singer shimmies across the stage at the speed of 1 foot every 10 seconds, while the bassist shuffles at the speed of 1 foot every 20 seconds. After 2 minutes, they both reach the edges of the stage. How wide is the stage?

Q4
A rowing boat travels at an average speed of
¹
⁄
₁₀₀₀
mile every second. How far will the boat travel in 2 hours?

Q5
A farmer leaves a bale of hay every morning at a location on Dartmoor for the wild ponies, while another farmer leaves a bucket of oats at another location in the evening. One pony starts at the hay and trots along a track to the location of the oats at a rate of 12 mph and remains at that location for the night. In the morning, he covers the same distance back to the hay at a rate of 6 mph. His round trip journey takes exactly 2 hours and he always starts the journey at the location of the hay. What is the distance between the location of the hay and the location of the oats?

Q6
On a particular stretch of railway line, a speed restriction of 50 per cent of the maximum speed of 100 mph is imposed on parts of the track. What is the minimum time a traveller must allow to complete a journey of 375 miles?

Q7
A hosepipe discharges water at a rate of 4 gallons per minute. How long, in hours, does it take to fill a paddling pool with a 300-gallon capacity?

Q8
Mike drives from his flat to the seaside in 1½ hours. On the way home he is in a hurry to watch the start of the Crystal Palace match and drives one and a half times as fast along the same route. How much time does he spend driving?

Q9
Two cars, 100 miles apart, set off driving towards each other. One is travelling at 70 mph and the other is travelling at 80 mph. After how long will the two cars meet?

Q10
A small car with an engine size of 848 cc and a family car with an engine size of 3 litres set off on a journey of 480 miles. The family car completes the journey in 8 hours. The small car travels at an average speed of 5⁄6 of the speed of the family car. How long after the family car will the small car arrive at the destination?

Q11
The perimeter of Jenny’s local park measures 5.5 miles and it takes Jenny 3 hours to run four times around the park. What is her average speed?

Q12
Jake rides his new tricycle for half an hour in the park and covers ¾ mile. What is his average speed in miles per hour?

Q13
Bob drives a cab in London. He picks up a passenger at Gatwick Airport on a Friday afternoon and drives 26 miles to a Central London location, a journey of 2 hours and 15 minutes. Then he drives an additional 4 miles to Waterloo station, which takes another 45 minutes. What is Bob’s average speed for the Friday afternoon journeys?

Q14
An egg timer contains 18,000 grains of sand. The sand passes at a consistent rate between the top and the bottom cylinders. After 2 minutes and 24 seconds, 14,400 grains of sand have passed through the middle. At what rate per minute does the sand pass through the timer?

Q15
In the Ironman Triathlon, athletes are expected to swim for 2.4 miles, cycle for 112 miles and run a full marathon distance of 26.2 miles. Justin enters the competition and is given the following split times for each leg of the competition: Swim: 48 minutes Cycle: 4 hours 59 minutes

Run: 6 hours 43 minutes

To the nearest miles per hour, what is Justin’s average speed for the triathlon?

Work rate problems

Work rate problems require that you work out the time involved to complete a specified number of jobs by a specified number of operators. This section shows you two methods to tackle these questions. Choose the method that is easiest for you, and use the second method to check your answer.

Worked example

Work rate formula 1

To find the combined time of two operators working together but independently on the same job at different rates, use the following formula:

If it takes Sue 2 hours to weed the garden and it takes Dave 4 hours to do the same task, how long does it take Sue and Dave to weed the garden when they work on the task together at their individual rates? Apply the formula and plug in the numbers: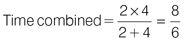

The task will take
⁸
⁄
₆
of an hour, or 1 hour 20 minutes.

Work rate formula 2

The total time required to complete a task by more than one operator is equivalent to the following formula:

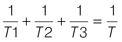
Worked example

If it takes Sue 2 hours to weed the garden and it takes Dave 4 hours to do the same task, how long does it take Sue and Dave to weed the garden when they work on the task together at their individual rates?

Apply the formula and plug in the numbers:

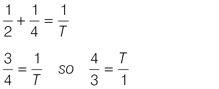
⁴
⁄
₃
× 60 minutes = 100 minutes, or 1 hour 20 minutes.

Work rates practice questions

Q1
Lisa paints a room in 2 hours and Amanda paints the same room in 3 hours. Working together but independently, how long does it take them to paint the room?

Q2
If Jake can clean his sister’s bike in 15 minutes and Lauren, Jake’s sister, can clean her own bike in 30 minutes, how many minutes will it take both of them together to clean Lauren’s bike?

Q3
Computer A can run a set of tasks in 1 hour while Computer B runs the same set of tasks in 1½ hours. How long will it take both computers working together to run half the set of tasks?

Answers to Chapter 3

Rates conversion: practice drill 1: time

Rates conversion: practice drill 2: distance