How to Pass Numerical Reasoning (21 page)
Read How to Pass Numerical Reasoning Online
Authors: Heidi Smith

Rates conversion: practice drill 2: distance
Set a stopwatch and aim to complete the following drill in three minutes.
Q1 | 25 mm | = | metres |
Q2 | 2 cm | = | km |
Q3 | 72 inches | = | feet |
Q4 | 1598 cm | = | km |
Q5 |
| = | foot |
Q6 | 956 cm | = | km |
Q7 | 12.91 cm | = | metres |
Q8 | 83 cm | = | mm |
Q9 | 39 inches | = | feet |
Q10 | 6 mm | = | km |
Rates conversion: practice drill 3: temperature
Set a stopwatch and aim to complete the following drill in three minutes. Convert the following temperatures to the nearest whole number:
Q1 | 32°C | = | °F |
Q2 | 37.5°C | = | °F |
Q3 | 3°C | = | °F |
Q4 | 572°C | = | °F |
Q5 | 0.25°C | = | °F |
Q6 | 99.68°F | = | °C |
Q7 | 5°F | = | °C |
Q8 | 8°F | = | °C |
Q9 | 98.6°F | = | °C |
Q10 | 105°F | = | °C |
A rate is a ratio, which establishes the relationship between two or more different quantities measured in different units. For example, you are probably familiar with the frequently used rates of ‘miles per gallon’ or ‘miles per hour’. Rates are used to measure proportions between different units and are a useful method to compare quantities of the different units, for example ‘cost per square metre’. This chapter will demonstrate how to substitute the variables into a common formula. The examples use time, speed and distance to demonstrate the concept. Hints on how to recognize other variables you may come across in the test are also provided.
There are three parts to a speed-distance-time problem. The key to answering these questions correctly is to identify the pieces correctly and substitute the information to the relevant formulae. The relationship between the three pieces of the puzzle is expressed as: Distance = Rate × Time
This can be rearranged as:

Or in other words:

The following sections work through examples of the use of each of the formulae.
Find the distance when you know the time and rate
Distance = Rate × Time
Worked example
A car travels along a country road at a rate of 45 mph for 5½ hours. How far does the car travel?
Estimate the answer
If the car travelled at 40 mph for 5 hours, the distance travelled would be:
40 mph × 5 hours = 200 miles.
As the actual speed is quicker and the time spent travelling longer, your answer will be slightly higher than 200.
Calculate the answer
Apply the formula to find the distance:
Rate | × | Time | = | Distance |
45 mph | × | 5.5 hours | = | 247.5 miles |
Distance travelled = 247.5 miles.
Worked example
Ruth sets out to paddle the Colorado River through the Grand Canyon. She paddles for 2 hours at a rate of 8.25 miles per hour while the river is calm. On approaching her first set of rapids, her speed increases to 18.5 miles per hour for half an hour until she reaches her first waterfall. How far is Ruth from her launch point when she reaches her first waterfall?
Estimate the answer
There are two speeds to consider here, and therefore you will calculate the distance in two stages. If Ruth travelled for 2 hours at 8 mph, she would travel 16 miles. If she travelled a further hour at 18 mph, she would travel 18 miles, so in half an hour she would travel for 9 miles. The total distance travelled therefore is approximately 16 miles + 9 miles = 25 miles.
Calculate the answer
Apply the formula to find the distance for each leg of the journey
Rate | × | Time | = | Distance |
8.25 mph | × | 2 hours | = | 16.5 miles |
18.5 mph | × | 0.5 hours | = | 9.25 miles |
Total distance travelled = 16½ + 9¼ = 25¾ miles.
Find the time when you know the distance and rate

Worked example
Iain lives on a small island off the West Coast of Scotland and rows his boat to the mainland once a week to collect provisions. The distance from the mooring point on the island to the mooring point on the mainland is half a mile. He rows his boat at a rate of 2 miles an hour when the wind is still. How many minutes does it take Iain to row to the mainland on a calm day?
Estimate the answer
If Iain rows for an hour, he will travel 2 miles. Since you know that the total distance he has to travel is less than 2 miles, you know that he will not be rowing for a whole hour.
Calculate the answer
Apply the formula and plug in the numbers:
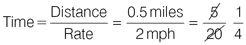
It takes Iain ¼ of an hour, or 15 minutes, to row to the mainland on a calm day.
Worked example
Captain Bengel is a jump-jet pilot based in the desert in Arizona. On one particular exercise, Bengel and his wingman, Captain Danger, set off from their airbase in Arizona to fly 320 miles to Las Vegas in Nevada at a constant average speed of 800 mph. On the return journey, the pilots are forced to reduce their speed to conserve fuel and return at a rate of 400 mph. What is the total flying time for both pilots together in hours and minutes, assuming simultaneous take-off and landing?
Estimate the answer
At a speed of 800 mph, the pilots would travel 800 miles in an hour, so the outbound journey of less than 320 miles will take a little less than half an hour. On the return journey of 320 miles at a speed of 400 mph, the journey would take a little less than an hour. The total flying time will therefore be (approximately ½ hour) + (approximately 1 hour) = approximately 1½ hours.
Calculate the answer
Apply the formula to find the time for both the outbound and inbound journeys.
Outbound journey:
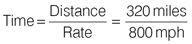
Reduce the fraction to its lowest terms:
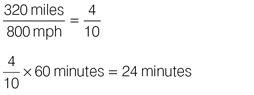
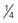 inch
inch