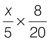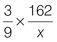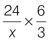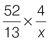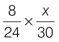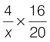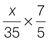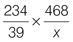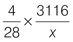How to Pass Numerical Reasoning (37 page)
Read How to Pass Numerical Reasoning Online
Authors: Heidi Smith

Q3
It takes 1 hour 20 minutes to bake a potato and 45 minutes to bake a pie. What is the ratio of time taken to bake a potato to time taken to bake a pie?
Q4
Dave’s training schedule requires him to increase his weekly mileage by 50 miles every week. In Week 2 he cycles 250 miles. What is the ratio of miles cycled in week 2 to miles cycled in week 3?
Q5
What is the ratio of currants to sultanas in a fruitcake consisting of 1 lb 2 oz currants and 12 oz sultanas? (There are 16 oz in 1 lb.)
Q6
In a musical ensemble, the ratio of stringed instruments to all other instruments is 8 : 3. What is the ratio of stringed instruments to all instruments in the ensemble?
Q7
At a rock concert, 250 out of the capacity crowd of 30,000 are left-handed. What fraction of the crowd is right-handed? (Assume that no one in the crowd is ambidextrous!)
Q8
In a certain yoga class of 32 attendees, 8 can stand on their heads unaided. What is the ratio of those who can stand unaided on their heads to those who can’t?
Q9
In a restaurant, the ratio of vegetarians to meat-eaters is 3 to 5. Of the vegetarians,
2
⁄
3
eat fish. What is the ratio of vegetarians to vegetarian fish-eaters to meat-eaters?
Q10
The ratio of cups to mugs on a table is 1 : 6. If ¼ of the cups and
2
⁄
3
of the mugs are filled with tea, and all the other cups and mugs are filled with coffee, what is the ratio of tea to all the drinks on the table?
The following questions require that you use a ratio to calculate actual values.
Q11
On a world atlas, ½ cm represents 250 miles. What is the distance represented by 2¾ cm?
Q12
A company issues dividend payments to two shareholders, Anne and Paula, in the ratio 5 : 4. Anne receives £225. How much does Paula receive?
Q13
Burnford hockey club ‘games won’ to ‘games lost’ record last season was 2 : 3. How many games did they play last season if all the games were either won or lost and Burnford won 6 games?
Q14
Charlotte ran a marathon (26.2 miles) in 4 hours and 30 minutes. She ran the first half in
4
⁄
5
of the time it took to run the second half. How long did the first half take?
Q15
In Factory A, the ratio of paper clip production to pencil sharpener production is 400 to 1 and the ratio of pencil sharpener production to stapler production is 3 to 5. What is the ratio of paper clip production to stapler production?
When you compare two equivalent ratios of equal value you are finding a proportion. You can think of proportions as ratios reduced to the simplest terms. For example, if you simplify the ratio 30 computers to 48 televisions you are finding a proportion.
When you know how to work with proportions, you can check easily whether two ratios are equal, find missing terms in a ratio, work out the greater of two ratios and work out proportional changes to a ratio. Knowledge of proportions is a good trick to have up your sleeve in an aptitude test. Swift multiplication of the elements in a proportion will help you to verify the answer to a ratio problem quickly.
Worked example: Method 1
In a proportion, the product of the
outer
terms equals the product of the
inner
terms. Does the ratio 24 apples to 36 apples equal the ratio 2 apples to 3 apples?
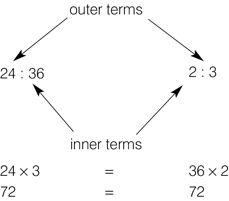
The proportions are equivalent.
Worked example: Method 2
Another way to think about proportions is to set up the ratios as fractions and cross-multiply. Are the following ratios equal: 25 pencils to 5 fountain pens = 100 pencils to 20 fountain pens?
Set up the ratios as fractions.
Tip: It doesn’t matter which unit is the numerator, as long as both sides of the equation have the same unit as the numerator.
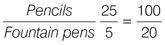
Cross-multiply the fractions

The ratios are equal, as both sides when cross-multiplied produce the same result. The ratios therefore form a proportion.
Tip
:
a
/
b
=
x
/
y
is the same as
a
:
b
=
x
:
y
.
Worked example
Is
2
⁄
3
greater than
8
⁄
13
? (Is
2
⁄
3
>
8
⁄
13
?) To answer the question, cross-multiply the numerators and denominators:
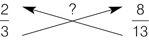
Follow the arrows and write down your answers at the end of the arrowhead.

Now ask, ‘Is 26 > 24?’ The answer is ‘yes’, so you know that
2
⁄
3
>
8
⁄
13
.
Worked example
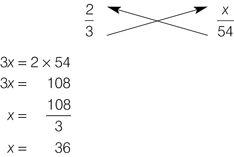
Use method 2 to find the missing term.
What is the value of
x
in the following proportion: 2 : 3 =
x
: 54?
Set up the ratios as fractions and cross-multiply.
Proportions: practice drill 1
Set a stopwatch and aim to complete the following drill in two minutes. Are the following proportions equivalent?
Q1 | 3 : 7 | and | 9 : 21 |
Q2 | 2 : 5 | and | 3 : 7 |
Q3 | 2 : 5 | and | 4 : 10 |
Q4 | 12 : 92 | and | 3 : 23 |
Q5 | 5 : 27 | and | 12 : 65 |
Q6 | 36 : 54 | and | 6 : 9 |
Q7 | 3 : 19 | and | 12 : 72 |
Q8 | 2 : 7 | and | 12 : 41 |
Q9 | 7 : 12 | and | 14 : 24 |
Q10 | 4 : 124 | and | 3 : 95 |
Proportions: practice drill 2
Set a stopwatch and aim to complete the following drill in two minutes. Find the missing terms in the following proportions.
Q1 |
| Q2 |
|
Q3 |
| Q4 |
|
Q5 |
| Q6 |
|
Q7 |
| Q8 |
|
Q9 |
| Q10 |
|