How to Pass Numerical Reasoning (36 page)

Ratios converter drill 2

Set a stopwatch and aim to complete the following drill in 1 minute. Express the following ratios, given in the format x : y, as fractions in their lowest form.

Types of ratio

Two types of ratio are typically tested in numeracy tests. These are ‘part to part’ ratios and ‘part to whole’ ratios. When you think about the ‘whole’ and the ‘part’ with ratios, think of the ‘whole’ as the complete set (or the ‘parent set’) and the ‘part’ as a subset of the parent set. For example, players in a football squad are the complete set (the whole) and those players picked for the starting line-up are the subset (the part). Once you understand how these ratios work, you can use ratios to determine actual values, for example the exact number of players in the squad.

‘Part to part’ ratios

Worked example

There are four oak trees for every two willow trees. What is the ratio of willows to oaks?

‘Types of trees’ is the parent set, and consists of two subsets, ‘willows’ and ‘oaks’.

Willows to Oaks = 2 : 4

Divide both sides by 2 to express the ratio in its simplest form:

Willows to Oaks = 1 : 2

‘Part to whole’ ratios

If you know the ratio of subsets to the complete set, you can work out the number of parts in the whole. You can also convert the ‘part to part’ ratio to a ‘part to whole’ ratio only when you are sure that there are no missing parts.

Worked example

A filing cabinet in Whitehall contains only files classified as ‘secret’ or ‘top secret’. The ratio of ‘secret’ to ‘top secret’ files in the filing cabinet is 3 : 2. What is the ratio of ‘top secret’ files to all files in the cabinet?

The parent set is ‘all files in the filing cabinet’ and consists of two subsets, ‘secret files’ and ‘top secret files’. You are given a ‘part to part’ ratio and asked to express one part as a subset of the whole. As there are only ‘secret’ and ‘top secret’ files in the filing cabinet, you can convert the ‘part to part’ ratio to a ‘part to whole’ ratio:

This tells you that for every five files, three are classified as ‘secret’ and two are classified as ‘top secret’. The ratio of top secret files to all files is therefore: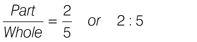

Note that this does not give you actual values (the number of files), just the ratio between quantities.

Worked example

A software company decides to expand its floor area by building additional floors underground for the software testers. When the construction is finished, one in four of the total floors in the building will be underground. What is the ratio of floors above ground to floors underground?

The floors can only be underground or above ground, so you can be sure to know all the subsets of the parent set. Therefore you can determine the part to whole ratio. The question tells you that for every floor underground, three are above ground. If ¼ of all floors are below ground, then ¾ must be above ground. The ratio of floors above ground to floors below is ¾ to ¼. Both quantities are expressed as quarters, so you can form a ratio with the numerators: Floors above ground to floors below ground = 3 : 1.

Using ratios to find actual quantities

A frequently tested concept is the use of ratios to find actual quantities. Ratios only tell you the relationship between numbers, not actual quantities. However, if you know the actual quantity of either a part or the whole, you can determine the actual quantity of the other parts.

Worked example

In a bag of 60 green and red jellybeans, the ratio of red jellybeans to green jellybeans is 2 : 3. How many are red?

Method 1

The parent set (the whole) is ‘all jellybeans in the bag’. The subsets (the parts) are ‘red jellybeans’ and ‘green jellybeans’. You know the actual value of the whole and the ratio between the parts, so you can work out the actual values of each part:

This tells you that for every 5 parts, 2 are red and 3 are green. To find the actual quantity of red jellybeans, multiply the ratio of red jellybeans by the actual value of the whole.

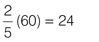
Method 2

You can solve this with simple algebra.

One part =
x
. Therefore 2
x
(red) + 3
x
(green) = 60 (all jellybeans).

5
x
= 60

x
= 60 ÷ 5 = 12

2
x
= 24 red jellybeans.

Worked example

A certain spice mix contains 66 g of a mix of cumin and coriander in the ratio of 4 :
x
. If 1 part cumin = 6 g, what is the ratio of cumin to coriander?

The parent set is ‘66 g of spice mix’ and consists of two subsets, cumin and coriander.

1 part cumin = 6 g, so 4 × 6 g cumin = 4 parts (24 g). If 24 g of the mix is cumin, then 66 g – 24 g (42 g) is coriander.

The ratio of actual quantities of cumin to coriander = 24 g : 42 g. Divide both sides by 6 to comply with the format of the ratio in the question: 24 : 42 = 4 : 7. The ratio of cumin to coriander is 4 : 7.

Worked example

At the Tedbury Rolling-Rollers, a race open to skaters and bladers, the ratio of skaters to all racers is 2 to 3. There are a total of 240 Rolling-Rollers in the race. How many are on skates?

You are given a ‘part to whole’ ratio and asked to work out the actual value of a part:

The total number of competitors is 240. Multiply the ratio (expressed as a fraction) by the actual value of the whole number to find the number of skaters: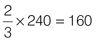

There are 160 skaters in the race.

Worked example

After a hot whites wash, the ratio of the pink socks to all socks emerging from the washing machine is 3 : 5. 15 pairs of socks were put in the washing machine at the start of the programme. How many socks are not pink at the end of the wash? (Assume that all the socks that go into the washing machine also come out of it.) 15 pairs of socks went into the washing machine = 30 socks. The question tells you that the ratio of pink socks to all socks = 3 : 5. Express the ratio as a fraction: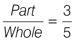

If
³
⁄
₅
of the socks are pink, then
²
⁄
₅
of the socks are not pink. Multiply
²
⁄
₅
by the actual value of the whole: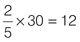

Number of non-pink socks = 12 (or 6 pairs).

Ratios practice questions

Give all your answers in the ratio format x : y.

Q1
In a school there is one qualified teacher for every 32 students. What is the ratio of students to qualified teachers?

Q2
Last season, Southwold United won 18 games and lost 9 games. What is the ratio of games lost to games won?