How to Pass Numerical Reasoning (4 page)

Long division: practice drill 2

Set a stopwatch and aim to complete the following practice drill within five minutes.

Prime numbers

An integer greater than 1 is a prime number if its only positive divisors are itself and 1. All prime numbers apart from 2 are odd numbers. Even numbers are divisible by 2 and cannot be prime by definition. 1 is not a prime number, because it is divisible by one number only, itself. The following is a list of all the prime numbers below 100. It’s worth becoming familiar with these numbers so that when you come across them in your test, you don’t waste time trying to find other numbers to divide into them!

Prime numbers: practice drill

Refer to the table above to assist you with the following drill:

Q1
What is the product of the first four prime numbers?

Q2
What is the sum of the prime numbers between 40 and 50 minus the eleventh prime number?

Q3
How many prime numbers are there?

Q4
How many prime numbers are there between 1 and 100?

Q5
What is the only even prime number?

Q6
Between 1 and 100, there are five prime numbers ending in 1. What are they?

Q7
What is the result of the product of the first three prime numbers minus the sum of the second three prime numbers?

Q8
How many prime numbers are there between 60 and 80?

Q9
How many prime numbers are there between 90 and 100?

Q10
What is the sum of the second 12 prime numbers minus the sum of the first 12 prime numbers?

Multiples

A
multiple
is a number that divides by another without a remainder. For example, 54 is a multiple of 9 and 72 is a multiple of 8.

Tips to find multiples

An integer is divisible by:

2, if the last digit is 0 or is an even number

3, if the sum of its digits are a multiple of 3

4, if the last two digits are a multiple of 4

5, if the last digit is 0 or 5

6, if it is divisible by 2 and 3

9, if its digits sum to a multiple of 9

There is no consistent rule to find multiples of 7 or 8.

Worked example

Is 2,648 divisible by 2? Yes, because 8 is divisible by an even number.

Is 91,542 divisible by 3? Yes, because 9+1+5+4+2 = 21 and 21 is a multiple of 3.

Is 216 divisible by 4? Yes, because 16 is a multiple of 4.

Is 36,545 divisible by 5? Yes, because the last digit is 5.

Is 9,918 divisible by 6? Yes, because the last digit, 8, is divisible by an even number and the sum of all the digits, 27, is a multiple of 3.

Multiples: practice drill

Set a stopwatch and aim to complete the following 10-question drill in five minutes.

The following numbers are multiples of which of the following integers: 2, 3, 4, 5, 6, 9?

Lowest common multiple

The
lowest common multiple
is the least quantity that is a multiple of two or more given values. To find a multiple of two integers, you can simply multiply them together, but this will not necessarily give you the lowest common multiple of both integers. To find the lowest common multiple, you will work with the prime numbers. This is a concept you will find useful when working with fractions. There are three steps to find the lowest common multiple of two or more numbers: Step 1: Express each of the integers as the product of its prime factors.

Step 2: Line up common prime factors.

Step 3: Find the product of the distinct prime factors.

Worked example

What is the lowest common multiple of 6 and 9?

Step 1: Express each of the integers as the product of its prime factors

To find the prime factors of an integer, divide that number by the prime numbers, starting with 2. The product of the prime factors of an integer is called the prime factorization.

Divide 6 by 2:

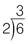
Now divide the remainder, 3, by the next prime factor after 2:

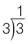
So the prime factors of 6 are
2
and
3
. (Remember that 1 is not a prime number.) The product of the prime factors of an integer is called the prime factorization, so the prime factorization of 6 = 2 × 3.

Now follow the same process to work out the prime factorization of 9 by the same process. Divide 9 by the first prime number that divides without a remainder: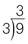

Now divide the result by the first prime number that divides without a remainder.

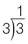
The prime factorization of 9 = 3 × 3.

Step 2: Line up common prime factors

Line up the prime factors of each of the given integers below each other:

6 = 2 × 3

9 = 3 × 3

Notice that 6 and 9 have a common prime factor (3).

Step 3: Find the product of the prime factors

Multiply all the prime factors together. When you see a common prime factor, count this only once.