Hyperspace (28 page)

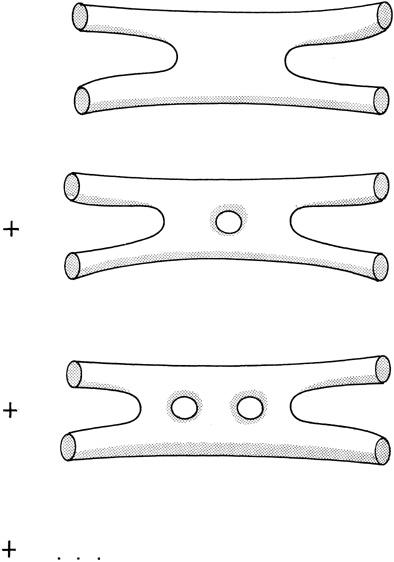
Figure 7.1. In string theory, the gravitational force is represented by the exchange of closed strings, which sweep out tubes in space-time. Even if we add up an infinite series of diagrams with a large number of holes, infinities never appear in the theory, giving us a finite theory of quantum gravity
.

Intrigued by the program being initiated by KSV, I decided to try my luck at solving the problem. This was a bit difficult, because I was dodging machine-gun bullets at the time.

I remember clearly when the KSV paper came out in 1969. KSV was proposing a program for future work, rather than giving precise details. I decided then to calculate all possible loops explicitly and complete the KSV program.

It’s hard to forget those times. There was a war raging overseas, and the university campuses from Kent State to the University of Paris, were in a state of turmoil. I had graduated from Harvard the year before, when President Lyndon Johnson revoked deferments for graduate students, sending panic throughout graduate schools in the country. Chaos gripped the campuses. Suddenly, my friends were dropping out of college, teaching high school, packing their bags and heading to Canada, or trying to ruin their health in order to flunk the army physical.

Promising careers were being shattered. One of my good friends in physics from MIT vowed that he would go to jail rather than fight in Vietnam. He told us to send copies of the
Physical Review
to his jail cell so he could keep up with developments in the Veneziano model. Other friends, who quit college to teach in high schools rather than fight in the war, terminated promising scientific careers. (Many of them still teach in these high schools.)

Three days after graduation, I left Cambridge and found myself in the United States Army stationed at Fort Benning, Georgia (the largest infantry training center in the world), and later at Fort Lewis, Washington. Tens of thousands of raw recruits with no previous military training were being hammered into a fighting force and then shipped to Vietnam, replacing the 500 GIs who were dying every week.

One day, while throwing live grenades under the grueling Georgia sun and seeing the deadly shrapnel scatter in all directions, my thoughts began to wander. How many scientists throughout history had to face the punishing ravages of war? How many promising scientists were snuffed out by a bullet in the prime of their youth?

I remembered that Karl Schwarzschild had died in the kaiser’s army on the Russian front during World War I just a few months after he found the basic solution to Einstein’s equations used in every black hole calculation. (The Schwarzschild radius of a black hole is named in his
honor. Einstein addressed the Prussian Academy in 1916 to commemorate Schwarzschild’s work after his untimely death at the front lines.) And how many promising people were cut down even before they could begin their careers?

Infantry training, I discovered, is rigorous; it is designed to toughen the spirit and dull the intellect. Independence of thought is ground out of you. After all, the military does not necessarily want some wit who will question the sergeant’s orders in the middle of a firefight. Understanding this, I decided to bring along some physics papers. I needed something to keep my mind active while peeling potatoes in KP or firing machine guns, so I brought along a copy of the KSV paper.

During night infantry training, I had to go past an obstacle course, which meant dodging live machine-gun bullets, froglegging under barbed wire, and crawling through thick brown mud. Because the automatic fire had tracers on them, I could see the beautiful crimson streaks made by thousands of machine-gun bullets sailing a few feet over my head. However, my thoughts kept drifting back to the KSV paper and how their program could be carried out.

Fortunately, the essential feature of the calculation was strictly topological. It was clear to me that these loops were introducing an entirely new language to physics, the language of topology. Never before in the history of physics had Möbius strips or Klein bottles been used in a fundamental way.

Because I rarely had any paper or pencils while practicing with machine guns, I forced myself to visualize in my head how strings could be twisted into loops and turned inside out. Machine-gun training was actually a blessing in disguise because it forced me to manipulate large blocks of equations in my head. By the time I finished the advanced machine-gun-training program, I was convinced that I could complete the program of calculating all loops.

Finally, I managed to squeeze time from the army to go to the University of California at Berkeley, where I furiously worked out the details that were racing in my head. I sank several hundred hours of intense thought into the question. This, in fact, became my Ph.D. dissertation.

By 1970, the final calculation took up several hundred densely filled notebook pages. Under the careful supervision of my adviser, Stanley Mandelstam, my colleague Loh-ping Yu and I successfully calculated an explicit expression for all possible loop diagrams known at that time. However, I wasn’t satisfied with this work. The KSV program consisted of a hodge-podge of rules of thumb and intuition, not a rigorous set of basic principles from which these loops could be derived. String theory,
we saw, was evolving backward, since its accidental discovery by Veneziano and Suzuki. The next step in the backward evolution of the string was to follow in the footsteps of Faraday, Riemann, Maxwell, and Einstein and construct a
field theory of strings
.

Ever since the pioneering work of Faraday, every physical theory had been written in terms of fields. Maxwell’s theory of light was based on field theory. So was Einstein’s. In fact, all of particle physics was based on field theory. The only theory
not
based on field theory was string theory. The KSV program was more a set of convenient rules than a field theory.

My next goal was to rectify that situation. The problem with a field theory of strings, however, was that many of the pioneering figures in physics argued against it. Their arguments were simple. These giants of physics, such as Hideki Yukawa and Werner Heisenberg, had labored for years to create a field theory that was not based on point particles. Elementary particles, they thought, might be pulsating blobs of matter, rather than points. However, no matter how hard they tried, field theories based on blobs always violated causality.

If we were to shake the blob at one point, the interactions would spread faster than the speed of light throughout the blob, violating special relativity and creating all sorts of time paradoxes. Thus “nonlocal field theories” based on blobs were known to be a monstrously difficult problem. Many physicists, in fact, insisted that only local field theories based on point particles could be consistent. Nonlocal field theories must violate relativity.

The second argument was even more convincing. The Veneziano model had many magical properties (including something called
duality
) that had never been seen before in field theory. Years earlier, Richard Feynman had given “rules” that any field theory should obey. However, these Feynman rules were in direct violation of duality. Thus many string theorists were convinced that a field theory of strings was impossible because string theory necessarily violated the properties of the Veneziano model. String theory, they said, was unique in all of physics because it could not be recast as a field theory.

I collaborated with Keiji Kikkawa on this difficult but important problem. Step by step we built our field theory, in much the same way that our predecessors had constructed field theories for other forces. Following
Faraday, we introduced a field at every point in space-time. However, for a field theory of strings, we had to generalize the concept of Faraday and postulate a field that was defined for all possible configurations of a string vibrating in space-time.

The second step was to postulate the field equations that the string obeyed. The field equation for a single string moving alone in space-time was easy. As expected, our field equations reproduced an infinite series of string resonances, each corresponding to a subatomic particle. Next, we found that the objections of Yukawa and Heisenberg were solved by string field theory. If we jiggled the string, the vibrations traveled down the string at less than the speed of light.

Soon, however, we hit a brick wall. When we tried to introduce interacting strings, we could not reproduce the Veneziano amplitude correctly. Duality and the counting of graphs given by Feynman for any field theory were in direct conflict. Just as the critics expected, the Feynman graphs were incorrect. This was disheartening. It appeared that field theory, which had formed the foundation of physics for the past century, was fundamentally incompatible with string theory.

Discouraged, I remember mulling over the problem late into the night. For hours, I began systematically to check all the possible alternatives to this problem. But the conclusion that duality had to be broken seemed inescapable. Then I remembered what Sherlock Holmes, in Arthur Conan Doyle’s “The Sign of Four,” said to Watson: “How often have I said to you that when you have eliminated the impossible, whatever remains,
however improbable
, must be the truth.” Encouraged by this idea, I eliminated all the impossible alternatives. The only improbable alternative remaining was to violate the properties of the Veneziano-Suzuki formula. At about 3:00
A.M
., the resolution finally hit me. I realized that physicists had overlooked the obvious fact that one can split the Veneziano-Suzuki formula into two pieces. Each part then corresponds to one of Feynman’s diagrams, and each part violates duality, but the
sum
obeys all the correct properties of a field theory.

I quickly took out some paper and went over the calculation. I spent the next 5 hours checking and rechecking the calculation from all possible directions. The conclusion was inescapable: Field theory does violate duality, as everyone expected, but this is acceptable because the final sum reproduces the Veneziano-Suzuki formula.

I had now solved most of the problem. However, one more Feynman diagram, representing the collision of four strings, was still lacking. That year, I was teaching introductory electricity and magnetism to undergraduates at the City University of New York, and we were studying Faraday’s
lines of force. I would ask the students to draw the lines of force emanating from different configurations of charges, repeating the same steps pioneered by Faraday in the nineteenth century. Suddenly, it dawned on me that the squiggly lines that I was asking my students to draw had exactly the same topological structure as the collision of strings. Thus by rearranging charges in a freshman laboratory, I had found the correct configuration describing the collision of four strings.

Was it that simple?

I rushed home to check my hunch, and I was right. By employing pictorial techniques that even a freshman can use, I could show that the four-string interaction must be hidden within the Veneziano formula. By the winter of 1974, using methods dating back to Faraday, Kikkawa and I completed the field theory of strings, the first successful attempt to combine string theory with the formalism of field theory.

Our field theory, although it correctly embodied the entire information contained within string theory, still needed improvement. Because we were constructing the field theory backward, many of the symmetries were still obscure. For example, the symmetries of special relativity were present but not in an obvious way. Much more work was needed to streamline the field equations we had found. But just as we were beginning to explore the properties of our field theory, the model unexpectedly suffered a severe setback.

That year, physicist Claude Lovelace of Rutgers University discovered that the bosonic string (describing integral spins) is self-consistent only in 26 dimensions. Other physicists verified this result and showed that the superstring (describing both integral and half-integral spin) is self-consistent only in ten dimensions. It was soon realized that, in dimensions other than ten or 26 dimensions, the theory completely loses all its beautiful mathematical properties. But no one believed that a theory defined in ten or 26 dimensions had anything to do with reality. Research in string theory abruptly ground to a halt. Like Kaluza-Klein theory before it, string theory lapsed into a deep hibernation. For 10 long years, the model was banished to obscurity. (Although most string physicists, myself included, abandoned the model like a sinking ship, a few die-hards, like physicists John Schwarz and the late Joel Scherk, tried to keep the model alive by steadily making improvements. For example, string theory was originally thought to be just a theory of the strong interactions, with each mode of vibration corresponding to a resonance of the quark model. Schwarz and Scherk correctly showed that the string model was really a unified theory of all forces, not just the strong interactions.)