In Pursuit of the Unknown (8 page)
Read In Pursuit of the Unknown Online
Authors: Ian Stewart

The tsunami overwhelmed the plant's defences, cutting the supply of electrical power. The three operating reactors (numbers 1, 2, and 3) were shut down as a safety measure, but their cooling systems were still needed to stop the fuel from melting. However, the tsunami also wrecked the emergency generators, which were intended to power the cooling system and other safety-critical systems. The next level of backup, batteries, quickly ran out of power. The cooling system stopped and the nuclear fuel in several reactors began to overheat. Improvising, the operators used fire engines to pump seawater into the three operating reactors, but this reacted with the zirconium cladding on the fuel rods to produce hydrogen. The build-up of hydrogen caused an explosion in the building housing Reactor 1. Reactors 2 and 3 soon suffered the same fate. The water in the pool of Reactor 4 drained out, leaving its fuel exposed. By the time the operators regained some semblance of control, at least one reactor containment vessel had cracked, and radiation was leaking out into the local environment. The Japanese authorities evacuated 200,000 people from the surrounding area because the radiation was well above normal safety limits. Six months later, the company operating the reactors, TEPCO, stated that the situation remained critical and much more work would be needed before the reactors could be considered fully under control, but claimed the leakage had been stopped.
I don't want to analyse the merits or otherwise of nuclear power here, but I do want to show how the logarithm answers a vital question: if you know how much radioactive material has been released, and of what kind, how long will it remain in the environment, where it could be hazardous?
Radioactive elements decay; that is, they turn into other elements through nuclear processes, emitting nuclear particles as they do so. It is these particles that constitute the radiation. The level of radioactivity falls away over time just as the temperature of a hot body falls when it cools:
exponentially. So, in appropriate units, which I won't discuss here, the level of radioactivity
N
(
t
) at time
t
follows the equation
N
(
t
) =
N
0
e
âkt
where N
0
is the initial level and
k
is a constant depending on the element concerned. More precisely, it depends on which form, or isotope, of the element we are considering.
A convenient measure of the time radioactivity persists is the half-life, a concept first introduced in 1907. This is the time it takes for an initial level N
0
to drop to half that size. To calculate the half-life, we solve the equation
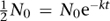
by taking logarithms of both sides. The result is
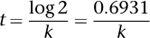
and we can work this out because
k
is known from experiments.
The half-life is a convenient way to assess how long the radiation will persist. Suppose that the half-life is one week, for instance. Then the original rate at which the material emits radiation halves after 1 week, is down to one quarter after 2 weeks, one eighth after 3 weeks, and so on. It takes 10 weeks to drop to one thousandth of its original level (actually 1/1024), and 20 weeks to drop to one millionth.
In accidents with conventional nuclear reactors, the most important radioactive products are iodine-131 (a radioactive isotope of iodine) and caesium-137 (a radioactive isotope of caesium). The first can cause thyroid cancer, because the thyroid gland concentrates iodine. The half-life of iodine-131 is only 8 days, so it causes little damage if the right medication is available, and its dangers decrease fairly rapidly unless it continues to leak. The standard treatment is to give people iodine tablets, which reduce the amount of the radioactive form that is taken up by the body, but the most effective remedy is to stop drinking contaminated milk.
Caesium-137 is very different: it has a half-life of 30 years. It takes about 200 years for the level of radioactivity to drop to one hundredth of its initial value, so it remains a hazard for a very long time. The main practical issue in a reactor accident is contamination of soil and buildings. Decontamination is to some extent feasible, but expensive. For example, the soil can be removed, carted away, and stored somewhere safe. But this creates huge amounts of low-level radioactive waste.
Radioactive decay is just one area of many in which Napier's and Briggs's logarithms continue to serve science and humanity. If you thumb through later chapters you will find them popping up in thermodynamics and information theory, for example. Even though fast computers have now made logarithms redundant for their original purpose, rapid calculations, they remain central to science for conceptual rather than computational reasons.
Another application of logarithms comes from studies of human perception: how we sense the world around us. The early pioneers of the psychophysics of perception made extensive studies of vision, hearing, and touch, and they turned up some intriguing mathematical regularities.
In the 1840s a German doctor, Ernst Weber, carried out experiments to determine how sensitive human perception is. His subjects were given weights to hold in their hands, and asked when they could tell that one weight felt heavier than another. Weber could then work out what the smallest detectable difference in weight was. Perhaps surprisingly, this difference (for a given experimental subject) was not a fixed amount. It depended on how heavy the weights being compared were. People didn't sense an absolute minimum difference â 50 grams, say. They sensed a
relative
minimum difference â 1% of the weights under comparison, say. That is, the smallest difference that the human senses can detect is proportional to the stimulus, the actual physical quantity.
In the 1850s Gustav Fechner rediscovered the same law, and recast it mathematically. This led him to an equation, which he called Weber's law, but nowadays it is usually called Fechner's law (or the WeberâFechner law if you're a purist). It states that the perceived sensation is proportional to the
logarithm
of the stimulus. Experiments suggested that this law applies not only to our sense of weight but to vision and hearing as well. If we look at a light, the brightness that we perceive varies as the logarithm of the actual energy output. If one source is ten times as bright as another, then the difference we perceive is constant, however bright the two sources really are. The same goes for the loudness of sounds: a bang with ten times as much energy sounds a fixed amount louder.
The WeberâFechner law is not totally accurate, but it's a good approximation. Evolution pretty much had to come up with something like a logarithmic scale, because the external world presents our senses with stimuli over a huge range of sizes. A noise may be little more than a mouse scuttling in the hedgerow, or it may be a clap of thunder; we need to
be able to hear both. But the range of sound levels is so vast that no biological sensory device can respond in proportion to the energy generated by the sound. If an ear that could hear the mouse did that, then a thunderclap would destroy it. If it tuned the sound levels down so that the thunderclap produced a comfortable signal, it wouldn't be able to hear the mouse. The solution is to compress the energy levels into a comfortable range, and the logarithm does exactly that. Being sensitive to proportions rather than absolutes makes excellent sense, and makes for excellent senses.
Our standard unit for noise, the decibel, encapsulates the WeberâFechner law in a definition. It measures not absolute noise, but relative noise. A mouse in the grass produces about 10 decibels. Normal conversation between people a metre apart takes place at 40â60 decibels. An electric mixer directs about 60 decibels at the person using it. The noise in a car, caused by engine and tyres, is 60â80 decibels. A jet airliner a hundred metres away produces 110â140 decibels, rising to 150 at thirty metres. A vuvuzela (the annoying plastic trumpet-like instrument widely heard during the football World Cup in 2010 and brought home as souvenirs by misguided fans) generates 120 decibels at one metre; a military stun grenade produces up to 180 decibels.
Scales like these are widely encountered because they have a safety aspect. The level at which sound can potentially cause hearing damage is about 120 decibels. Please throw away your vuvuzela.
| 3 | Ghosts of departed quantities |
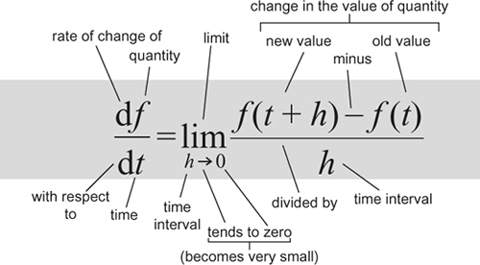
To find the instantaneous rate of change of a quantity that varies with (say) time, calculate how its value changes over a short time interval and divide by the time concerned. Then let that interval become arbitrarily small.
It provides a rigorous basis for calculus, the main way scientists model the natural world.
Calculation of tangents and areas. Formulas for volumes of solids and lengths of curves. Newton's laws of motion, differential equations. The laws of conservation of energy and momentum. Most of mathematical physics.
I
n 1665 Charles II was king of England and his capital city, London, was a sprawling metropolis of half a million people. The arts flourished, and science was in the early stages of an ever-accelerating ascendancy. The Royal Society, perhaps the oldest scientific society now in existence, had been founded five years earlier, and Charles had granted it a royal charter. The rich lived in impressive houses, and commerce was thriving, but the poor were crammed into narrow streets overshadowed by ramshackle buildings that jutted out ever further as they rose, storey by storey. Sanitation was inadequate; rats and other vermin were everywhere. By the end of 1666, one fifth of London's population had been killed by bubonic plague, spread first by rats and then by people. It was the worst disaster in the capital's history, and the same tragedy played out all over Europe and North Africa. The king departed in haste for the more sanitary countryside of Oxfordshire, returning early in 1666. No one knew what caused plague, and the city authorities tried everything â burning fires continually to cleanse the air, burning anything that gave off a strong smell, burying the dead quickly in pits. They killed many dogs and cats, which ironically removed two controls on the rat population.
During those two years, an obscure and unassuming undergraduate at Trinity College, Cambridge, completed his studies. Hoping to avoid the plague, he returned to the house of his birth, from which his mother managed a farm. His father had died shortly before he was born, and he had been brought up by his maternal grandmother. Perhaps inspired by rural peace and quiet, or lacking anything better to do with his time, the young man thought about science and mathematics. Later he wrote: âIn those days I was in the prime of my life for invention, and minded mathematics and [natural] philosophy more than at any other time since.' His researches led him to understand the importance of the inverse square law of gravity, an idea that had been hanging around ineffectually for at least 50 years. He worked out a practical method for solving problems in calculus, another concept that was in the air but had not been formulated in any generality. And he discovered that white sunlight is composed of many different colours â all the colours of the rainbow.