In Pursuit of the Unknown (6 page)
Read In Pursuit of the Unknown Online
Authors: Ian Stewart

How to multiply numbers by adding related numbers instead.
Addition is much simpler than multiplication.
Efficient methods for calculating astronomical phenomena such as eclipses and planetary orbits. Quick ways to perform scientific calculations. The engineers' faithful companion, the slide rule. Radioactive decay and the psychophysics of human perception.
N
umbers originated in practical problems: recording property, such as animals or land, and financial transactions, such as taxation and keeping accounts. The earliest known number notation, aside from simple tallying marks like ||||, is found on the outside of clay envelopes. In 8000
BC
Mesopotamian accountants kept records using small clay tokens of various shapes. The archaeologist Denise Schmandt-Besserat realised that each shape represented a basic commodity â a sphere for grain, an egg for a jar of oil, and so on. For security, the tokens were sealed in clay wrappings. But it was a nuisance to break a clay envelope open to find out how many tokens were inside, so the ancient accountants scratched symbols on the outside to show what was inside. Eventually they realised that once you had these symbols, you could scrap the tokens. The result was a series of written symbols for numbers â the origin of all later number symbols, and perhaps of writing too.
Along with numbers came arithmetic: methods for adding, subtracting, multiplying, and dividing numbers. Devices like the abacus were used to do the sums; then the results could be recorded in symbols. After a time, ways were found to use the symbols to perform the calculations without mechanical assistance, although the abacus is still widely used in many parts of the world, while electronic calculators have supplanted pen and paper calculations in most other countries.
Arithmetic proved essential in other ways, too, especially in astronomy and surveying. As the basic outlines of the physical sciences began to emerge, the fledgeling scientists needed to perform ever more elaborate calculations, by hand. Often this took up much of their time, sometimes months or years, getting in the way of more creative activities. Eventually it became essential to speed up the process. Innumerable mechanical devices were invented, but the most important breakthrough was a conceptual one: think first, calculate later. Using clever mathematics, you could make difficult calculations much easier.
The new mathematics quickly developed a life of its own, turning out to have deep theoretical implications as well as practical ones. Today, those early ideas have become an indispensable tool throughout science,
reaching even into psychology and the humanities. They were widely used until the 1980s, when computers rendered them obsolete for practical purposes, but, despite that, their importance in mathematics and science has continued to grow.
The central idea is a mathematical technique called a logarithm. Its inventor was a Scottish laird, but it took a geometry professor with strong interests in navigation and astronomy to replace the laird's brilliant but flawed idea by a much better one.
In March 1615 Henry Briggs wrote a letter to James Ussher, recording a crucial event in the history of science:
Napper, lord of Markinston, hath set my head and hands a work with his new and admirable logarithms. I hope to see him this summer, if it please God, for I never saw a book which pleased me better or made me more wonder.
Briggs was the first professor of geometry at Gresham College in London, and âNapper, lord of Markinston' was John Napier, eighth laird of Merchiston, now part of the city of Edinburgh in Scotland. Napier seems to have been a bit of a mystic; he had strong theological interests, but they mostly centred on the book of Revelation. In his view, his most important work was
A Plaine Discovery of the Whole Revelation of St John
, which led him to predict that the world would end in either 1688 or 1700. He is thought to have engaged in both alchemy and necromancy, and his interests in the occult lent him a reputation as a magician. According to rumour, he carried a black spider in a small box everywhere he went, and possessed a âfamiliar', or magical companion: a black cockerel. According to one of his descendants, Mark Napier, John employed his familiar to catch servants who were stealing. He locked the suspect in a room with the cockerel and instructed them to stroke it, telling them that his magical bird would unerringly detect the guilty. But Napier's mysticism had a rational core, which in this particular instance involved coating the cockerel with a thin layer of soot. An innocent servant would be confident enough to stroke the bird as instructed, and would get soot on their hands. A guilty one, fearing detection, would avoid stroking the bird. So, ironically, clean hands proved you were guilty.
Napier devoted much of his time to mathematics, especially methods for speeding up complicated arithmetical calculations. One invention,
Napier's bones, was a set of ten rods, marked with numbers, which simplified the process of long multiplication. Even better was the invention that made his reputation and created a scientific revolution: not his book on Revelation, as he had hoped, but his
Mirifici Logarithmorum Canonis Descriptio
(âDescription of the Wonderful Canon of Logarithms') of 1614. The preface shows that Napier knew exactly what he had produced, and what it was good for.
1
Since nothing is more tedious, fellow mathematicians, in the practice of the mathematical arts, than the great delays suffered in the tedium of lengthy multiplications and divisions, the finding of ratios, and in the extraction of square and cube roots â and . . . the many slippery errors that can arise: I had therefore been turning over in my mind, by what sure and expeditious art, I might be able to improve upon these said difficulties. In the end after much thought, finally I have found an amazing way of shortening the proceedings . . . it is a pleasant task to set out the method for the public use of mathematicians.
The moment Briggs heard of logarithms, he was enchanted. Like many mathematicians of his era, he spent a lot of his time performing astronomical calculations. We know this because another letter from Briggs to Ussher, dated 1610, mentions calculating eclipses, and because Briggs had earlier published two books of numerical tables, one related to the North Pole and the other to navigation. All of these works had required vast quantities of complicated arithmetic and trigonometry. Napier's invention would save a great deal of tedious labour. But the more Briggs studied the book, the more convinced he became that although Napier's strategy was wonderful, he'd got his tactics wrong. Briggs came up with a simple but effective improvement, and made the long journey to Scotland. When they met, âalmost one quarter of an hour was spent, each beholding the other with admiration, before one word was spoken'.
2
What was it that excited so much admiration? The vital observation, obvious to anyone learning arithmetic, was that adding numbers is relatively easy, but multiplying them is not. Multiplication requires many more arithmetical operations than addition. For example, adding two ten-digit numbers involves about ten simple steps, but multiplication requires 200. With modern computers, this issue is still important, but now it is tucked away behind the scenes in the algorithms used for multiplication.
But in Napier's day it all had to be done by hand. Wouldn't it be great if there were some mathematical trick that would convert those nasty multiplications into nice, quick addition sums? It sounds too good to be true, but Napier realised that it was possible. The trick was to work with powers of a fixed number.
In algebra, powers of an unknown
x
are indicated by a small raised number. That is,
xx
=
x
2
,
xxx
=
x
3
,
xxxx
=
x
4
, and so on, where as usual in algebra placing two letters next to each other means you should multiply them together. So, for instance, 10
4
= 10 Ã 10 Ã 10 Ã 10 = 10,000. You don't need to play around with such expressions for long before you discover an easy way to work out, say, 10
4
à 10
3
. Just write down
10,000 Ã 1,000 = (10 Ã 10 Ã 10 Ã 10) Ã (10 Ã 10 Ã 10)
= 10 Ã 10 Ã 10 Ã 10 Ã 10 Ã 10 Ã 10
= 10,000,000
The number of 0s in the answer is 7, which equals 4 + 3. The first step in the calculation shows
why
it is 4 + 3: we stick four 10s and three 10s next to each other. In short,
10
4
à 10
3
= 10
4+3
= 10
7
In the same way, whatever the value of
x
might be, if we multiply its
a
th power by its
b
th power, where
a
and
b
are whole numbers, then we get the (
a
+
b
)th power:
x
a
x
b
=
x
a+b
This may seem an innocuous formula, but on the left it multiplies two quantities together, while on the right the main step is to add
a
and
b
, which is simpler.
Suppose you wanted to multiply, say, 2.67 by 3.51. By long multiplication you get 9.3717, which to two decimal places is 9.37. What if you try to use the previous formula? The trick lies in the choice of
x
. If we take
x
to be 1.001, then a bit of arithmetic reveals that
(1.001)
983
= 2.67
(1.001)
1256
= 3.51
correct to two decimal places. The formula then tells us that 2.87 Ã 3.41 is
(1.001)
983+1256
= (1.001)
2239
which, to two decimal places, is 9.37.
The core of the calculation is an easy addition: 983 + 1256 = 2239. However, if you try to check my arithmetic you will quickly realise that if anything I've made the problem harder, not easier. To work out (1.001)
983
you have to multiply 1.001 by itself 983 times. And to discover that 983 is the right power to use, you have to do even more work. So at first sight this seems like a pretty useless idea.
Napier's great insight was that this objection is wrong. But to overcome it, some hardy soul has to calculate lots of powers of 1.001, starting with (1.001)
2
and going up to something like (1.001)
10,000
. Then they can publish a table of all these powers. After that, most of the work has been done. You just have to run your fingers down the successive powers until you see 2.67 next to 983; you similarly locate 3.51 next to 1256. Then you add those two numbers to get 2239. The corresponding row of the table tells you that this power of 1.001 is 9.37. Job done.
Really accurate results require powers of something a lot closer to 1, such as 1.000001. This makes the table far bigger, with a million or so powers. Doing the calculations for that table is a huge enterprise.
But it has to be done only once
. If some self-sacrificing benefactor makes the effort up front, succeeding generations will be saved a gigantic amount of arithmetic.
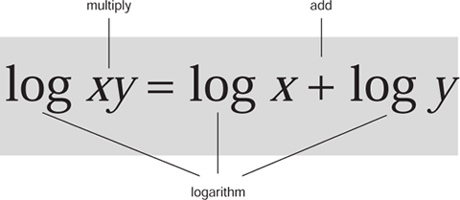
In the context of this example, we can say that the powers 983 and 1256 are the
logarithms
of the numbers 2.67 and 3.51 that we wish to multiply. Similarly 2239 is the logarithm of their product 9.38. Writing log as an abbreviation, what we have done amounts to the equation
log
ab
= log
a
+ log
b
which is valid for any numbers
a
and
b
. The rather arbitrary choice of 1.001 is called the
base
. If we use a different base, the logarithms that we calculate are also different, but for any fixed base everything works the same way.
This is what Napier should have done. But for reasons that we can only guess at, he did something slightly different. Briggs, approaching the technique from a fresh perspective, spotted two ways to improve on Napier's idea.