In Pursuit of the Unknown (2 page)
Read In Pursuit of the Unknown Online
Authors: Ian Stewart

The course of human history has been redirected, time and time again, by an equation. Equations have hidden powers. They reveal the innermost secrets of nature. This is not the traditional way for historians to organise the rise and fall of civilisations. Kings and queens and wars and natural disasters abound in the history books, but equations are thin on the ground. This is unfair. In Victorian times, Michael Faraday was demonstrating connections between magnetism and electricity to audiences at the Royal Institution in London. Allegedly, Prime Minister William Gladstone asked whether anything of practical consequence would come from it. It is said (on the basis of very little actual evidence, but why ruin a nice story?) that Faraday replied: âYes, sir. One day you will tax it.' If he did say that, he was right. James Clerk Maxwell transformed early experimental observations and empirical laws about magnetism and electricity into a system of equations for electromagnetism. Among the many consequences were radio, radar, and television.
An equation derives its power from a simple source. It tells us that two calculations, which appear different, have the same answer. The key symbol is the equals sign, =. The origins of most mathematical symbols are either lost in the mists of antiquity, or are so recent that there is no doubt where they came from. The equals sign is unusual because it dates back more than 450 years, yet we not only know who invented it, we even know
why
. The inventor was Robert Recorde, in 1557, in
The Whetstone of Witte
. He used two parallel lines (he used an obsolete word
gemowe
, meaning âtwin') to avoid tedious repetition of the words âis equal to'. He chose that symbol because âno two things can be more equal'. Recorde chose well. His symbol has remained in use for 450 years.
The power of equations lies in the philosophically difficult correspondence between mathematics, a collective creation of human minds, and an external physical reality. Equations model deep patterns in the outside world. By learning to value equations, and to read the stories
they tell, we can uncover vital features of the world around us. In principle, there might be other ways to achieve the same result. Many people prefer words to symbols; language, too, gives us power over our surroundings. But the verdict of science and technology is that words are too imprecise, and too limited, to provide an effective route to the deeper aspects of reality. They are too coloured by human-level assumptions. Words alone can't provide the essential insights.
Equations can. They have been a prime mover in human civilisation for thousands of years. Throughout history, equations have been pulling the strings of society. Tucked away behind the scenes, to be sure â but the influence was there, whether it was noticed or not. This is the story of the ascent of humanity, told through 17 equations.
| 1 | The squaw on the hippopotamus |
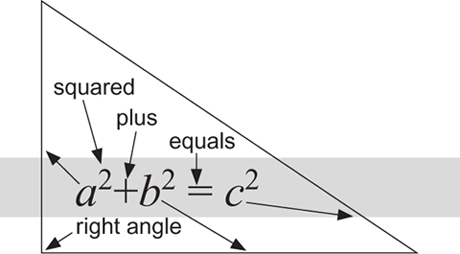
How the three sides of a right-angled triangle are related.
It provides a vital link between geometry and algebra, allowing us to calculate distances in terms of coordinates. It also inspired trigonometry.
Surveying, navigation, and more recently special and general relativity â the best current theories of space, time, and gravity.
A
sk any school student to name a famous mathematician, and, assuming they can think of one, more often than not they will opt for Pythagoras. If not, Archimedes might spring to mind. Even the illustrious Isaac Newton has to play third fiddle to these two superstars of the ancient world. Archimedes was an intellectual giant, and Pythagoras probably wasn't, but he deserves more credit than he is often given. Not for what he achieved, but for what he set in motion.
Pythagoras was born on the Greek island of Samos, in the eastern Aegean, around 570
BC
. He was a philosopher and a geometer. What little we know about his life comes from much later writers and its historical accuracy is questionable, but the key events are probably correct. Around 530
BC
he moved to Croton, a Greek colony in what is now Italy. There he founded a philosophico-religious cult, the Pythagoreans, who believed that the universe is based on number. Their founder's present-day fame rests on the theorem that bears his name. It has been taught for more than 2000 years, and has entered popular culture. The 1958 movie
Merry Andrew
, starring Danny Kaye, includes a song whose lyrics begin:
The square on the hypotenuse
of a right triangle
is equal to
the sum of the squares
on the two adjacent sides
.
The song goes on with some
double entendre
about not letting your participle dangle, and associates Einstein, Newton, and the Wright brothers with the famous theorem. The first two exclaim âEureka!'; no, that was Archimedes. You will deduce that the lyrics are not hot on historical accuracy, but that's Hollywood for you. However, in
Chapter 13
we will see that the lyricist (Johnny Mercer) was spot on with Einstein, probably more so than he realised.
Pythagoras's theorem appears in a well-known joke, with terrible puns about the squaw on the hippopotamus. The joke can be found all over the
internet, but it's much harder to discover where it came from.
1
There are Pythagoras cartoons, T-shirts, and a Greek stamp,
Figure 1
.

Fig 1
Greek stamp showing Pythagoras's theorem.
All this fuss notwithstanding, we have no idea whether Pythagoras actually
proved
his theorem. In fact, we don't know whether it was his theorem at all. It could well have been discovered by one of Pythagoras's minions, or some Babylonian or Sumerian scribe. But Pythagoras got the credit, and his name stuck. Whatever its origins, the theorem and its consequences have had a gigantic impact on human history. They literally opened up our world.
The Greeks did not express Pythagoras's theorem as an equation in the modern symbolic sense. That came later with the development of algebra. In ancient times, the theorem was expressed verbally and geometrically. It attained its most polished form, and its first recorded proof, in the writings of Euclid of Alexandria. Around 250
BC
Euclid became the first modern mathematician when he wrote his famous
Elements
, the most influential mathematical textbook ever. Euclid turned geometry into logic by making his basic assumptions explicit and invoking them to give systematic proofs for all of his theorems. He built a conceptual tower whose foundations were points, lines, and circles, and whose pinnacle was the existence of precisely five regular solids.
One of the jewels in Euclid's crown was what we now call Pythagoras's theorem: Proposition 47 of Book I of the
Elements
. In the famous
translation by Sir Thomas Heath this proposition reads: âIn right-angled triangles the square on the side subtending the right angle is equal to the squares on the sides containing the right angle.'
No hippopotamus, then. No hypotenuse. Not even an explicit âsum' or âadd'. Just that funny word âsubtend', which basically means âbe opposite to'. However, Pythagoras's theorem clearly expresses an equation, because it contains that vital word:
equal
.
For the purposes of higher mathematics, the Greeks worked with lines and areas instead of numbers. So Pythagoras and his Greek successors would decode the theorem as an equality of areas: âThe area of a square constructed using the longest side of a right-angled triangle is the sum of the areas of the squares formed from the other two sides.' The longest side is the famous hypotenuse, which means âto stretch under', which it does if you draw the diagram in the appropriate orientation, as in
Figure 2
(left).
Within a mere 2000 years, Pythagoras's theorem had been recast as the algebraic equation
a
2
+
b
2
=
c
2
where
c
is the length of the hypotenuse,
a
and
b
are the lengths of the other two sides, and the small raised 2 means âsquare'. Algebraically, the square of any number is that number multiplied by itself, and we all know that the area of any square is the square of the length of its side. So Pythagoras's equation, as I shall rename it, says the same thing that Euclid said â except for various psychological baggage to do with how the ancients thought about basic mathematical concepts like numbers and areas, which I won't go into.
Pythagoras's equation has many uses and implications. Most directly, it lets you calculate the length of the hypotenuse, given the other two sides. For instance, suppose that
a
= 3 and
b
= 4. Then
c
2
=
a
2
+
b
2
= 3
2
+ 4
2
= 9 + 16 = 25. Therefore
c
= 5. This is the famous 3â4â5 triangle, ubiquitous in school mathematics, and the simplest example of a Pythagorean triple: a list of three whole numbers that satisfies Pythagoras's equation. The next simplest, other than scaled versions such as 6â8â10, is the 5â12â13 triangle. There are infinitely many such triples, and the Greeks knew how to construct them all. They still retain some interest in number theory, and even in the last decade new features have been discovered.
Instead of using
a
and
b
to work out
c
, you can proceed indirectly, and solve the equation to obtain
a
provided that you know
b
and
c
. You can also answer more subtle questions, as we will shortly see.
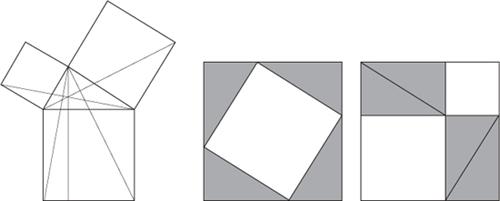
Fig 2
Left
: Construction lines for Euclid's proof of Pythagoras.
Middle
and
right
: Alternative proof of the theorem. The outer squares have equal areas, and the shaded triangles all have equal areas. Therefore the tilted white square has the same area as the other two white squares combined.
Why is the theorem true? Euclid's proof is quite complicated, and it involves drawing five extra lines on the diagram,
Figure 2
(left), and appealing to several previously proved theorems. Victorian schoolboys (few girls did geometry in those days) referred to it irreverently as Pythagoras's pants. A straightforward and intuitive proof, though not the most elegant, uses four copies of the triangle to relate two solutions of the same mathematical jigsaw puzzle,
Figure 2
(right). The picture is compelling, but filling in the logical details requires some thought. For instance: how do we know that the tilted white region in the middle picture is a square?