In the Beginning Was Information (26 page)
Read In the Beginning Was Information Online
Authors: Werner Gitt
Tags: #RELIGION / Religion & Science, #SCIENCE / Study & Teaching

If we limit the average information content of 4.32 bits for an amino acid (see chapter 6) to one letter (nucleotide) of the genetic code, then we find it to be 4.32:3 = 1.44 bits per letter. We can now express the statistical information density of DNA as follows, where 2 bits are taken as the information content of one letter (also see Table 3, genetic code, case a):
Ú = (0.94 x 10
21
letters/cm
3
) x (2 bits/letter) = 1.88 x 10
21
bits/cm
3
This packing density is so inconceivably great that we need an illustrative comparison. The photographic slide A in Figure 35 contains the entire Bible from Genesis to Revelation on its 33 mm x 32 mm surface, reproduced by means of special microfilm processes [M5]. From the computation given in [G11, p. 78–81], it follows that the DNA molecule entails a storage density 7.7 million million times as great as that of slide A which contains the entire Bible. If we want to obtain the DNA packing density on a photographic slide B, we would have to divide its surface into 2.77 million rows and 2.77 million columns and copy an entire Bible in a readable form in each of the tiny rectangles formed in this way. If this were possible, we would have reached the density of the information carried in each and every living cell. In any case, we should remember that it is technologically impossible to produce slide B, because all photographic techniques are limited to macroscopic reproductions and are unable to employ single molecules as units of storage. Even if it were possible to achieve such a photographic reduction, then we would still only have a static storage system, which differs fundamentally from that of DNA. The storage principle of DNA molecules is dynamic, since the contained information can be transferred unchanged to other cells by means of complex mechanisms.
These comparisons illustrate in a breathtaking way the brilliant storage concepts we are dealing with here, as well as the economic use of material and miniaturization. The highest known (statistical) information density is obtained in living cells, exceeding by far the best achievements of highly integrated storage densities in computer systems.
A1.3 Evaluation of Communication Systems
Technical communication systems:
After the discussion of Shannon’s definition of information in paragraph A1.1, the relevant question is: What is the use of a method which ignores the main principles of a phenomenon? The original and the most important application of Shannon’s information theory is given by the two so-called encoding theorems [S7]. These theorems state,
inter alia
, that in spite of the uncertainty caused by a perturbed communication link, the reception of a message could be certain. In other words, there exists an error-correcting method of encoding which assures greater message security with a given block (message) length.
Furthermore, the unit of measure, the bit, derived from Shannon’s definition of information, is fundamental to a quantitative assessment of information storage. It is also possible, at the statistical level, to compare directly given volumes of information which are encoded in various ways. This problem has been discussed fully in the previous paragraph A1.2.
Communication systems in living organisms:
Bernhard Hassenstein, a German biologist and cyberneticist, gave an impressive example illustrating both the brilliant concept of information transfer in living organisms, and its evaluation in terms of Shannon’s theory:
It is difficult, even frightening, to believe that the incomparable multiplicity of our experiences, the plethora of nuances — lights, colors, and forms, as well as the sounds of voices and noises …all the presentations of these in our sense receptor cells, are translated into a signaling language which is more monotonous than Morse code. Furthermore, this signaling language is the only basis through which the profusion of inputs is made alive in our subjective perception again — or for the first time. All our actions and activities are also expressed in this signaling language, from the fine body control of athletes to the hand movements of a pianist or the mood expressions of a concert hall performer.
Whatever we experience or do, all the impulses coursing through our nervous system from the environment to our consciousness and those traveling from our brain to the motor muscles, do so in the form of the most monotonous message system imaginable. The following novel question was only formulated when a scientific information concept had been developed, namely, what is the functional meaning of selecting a signaling language using the smallest number of symbols for the transmission of such a vast volume of information? This question could be answered practically immediately by means of the information concept of information theory.
The British physiologist W.H. Rushton was the first person to provide the answer which greatly surprised biologists, namely: There exists a result in information theory for determining the capacity of a communication system in such a way that its susceptibility to perturbating interference is minimized. This is known as the method of standardization of the properties of the impulses. The technique of pulse code modulation was discovered in the 1930s, but its theoretical principles were only established later. The symbolic language employed in living nervous systems corresponds exactly to the theoretical ideal of interference-free communication. It is impossible to improve on this final refinement of pulse code modulation, and the disadvantage of a diminished transmission capacity is more than offset by the increase in security. The monotonousness of the symbolic language of the nervous system thus convincingly establishes itself as expressing the highest possible freedom from interference. In this way, a very exciting basic phenomenon of physiology could be understood by means of the new concepts of information theory.
It should now be clear that Shannon’s information theory is very important for evaluating transmission processes of messages, but, as far as the message itself is concerned, it can only say something about its statistical properties, and nothing about the essential nature of information. This is its real weakness as well as its inherent propensity for leading to misunderstandings. The German cyberneticist Bernhard Hassenstein rightly criticizes it in the following words: "It would have been better to devise an artificial term, rather than taking a common word and giving it a completely new meaning." If we restrict Shannon’s information to one of the five aspects of information, then we do obtain a scientifically sound solution [G5]. Without the extension to the other four levels of information, we are stuck with the properties of a transmission channel. No science, apart from communication technology, should limit itself to just the statistical level of information.
Natural languages may be analyzed and compared statistically by means of Shannon’s theory, as we will now proceed to do.
A1.4 Statistical Analysis of Language
It is possible to calculate certain quantitative characteristics of languages by means of Shannon’s information theory. One example of such a property is the average information content of a letter, a syllable, or a word. In equation (9), this numerical value is denoted by
H
, the entropy.
1. Letters:
If, for the sake of simplicity, we assume that all 26 letters plus the space between words occur with the same frequency, then we have:
(11)
H
0
= lb 27 = log 27/log 2 = 4.755 bits/letter
It is known that the frequency of occurrence of the different letters is characteristic of the language we are investigating [B2 p 4]. The probability
p
i
of occurrence of single letters and the space are given for English and German in Table 1, as well as the average information content per letter, H. On applying equation (9) to the various letter frequencies P
i
in German, the average information content (= entropy) of a symbol is given by:
30
(12)
H
1
= ∑
p
i
x lb(1/
p
i
) = 4.112 95 bits/letter
i
=1
The corresponding value for English is
H
1
= 4.04577 bits per letter. We know that the probability of a single letter is not independent of the adjacent letters.
Q
is usually followed by
u
, and, in German,
n
follows
e
much more frequently than does
c
or
z
. If we also consider the frequency of pairs of letters (bigrams) and triplets (trigrams), etc., as given in Table 4, then the information content as defined by Shannon, decreases statistically because of the relationships between letters, and we have:
(13)
H
0
>
H
1
>
H
2
>
H
3
>
H
4
> ... >
H
oo
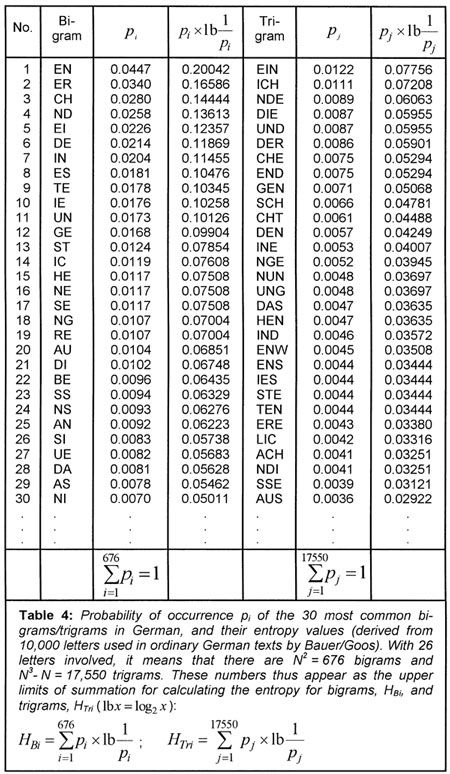 |
With 26 letters, the number of possible bigrams is 26
2
= 676, and there could be 26
3
- 26 = 17,550 trigrams, since three similar letters are never consecutive. Taking all statistical conditions into consideration, Küpfmüller [K4] obtained the following value for the German language:
(14)
H
oo
= 1.6 bits/letter
For a given language, the actual value of
H
0
is far below the maximum value of the entropy. The difference between the maximum possible value
H
max
and the actual entropy
H
, is called the redundance
R
. The relative redundance is calculated as follows:
(15)
r
= (
H
max
-
H
)/
H
max
For written German,
r
is given by (4.755 – 1.6)/4.755 = 66%. Brillouin obtained the following entropy values for English [B5]:
H
1
= 4.03 bits/letter
H
2
= 3.32 bits/letter
H
3
= 3.10 bits/letter
H
oo
= 2.14 bits/letter
We find that the relative redundance for English,
r
= (4.755 - 2.14)/4.755 = 55% is less than for German. In Figure 32 the redundancy of a language is indicated by the positions of the different points.
Languages usually employ more words than are really required for full comprehensibility. In the case of interference, certainty of reception is improved because messages usually contain some redundancy (e.g., illegibly written words, loss of signals in the case of a telegraphic message, or when words are not pronounced properly).
2. Syllables:
Statistical analyses of the frequencies of German syllables have resulted in the following value for the entropy when their frequency of occurrence is taken into account [K4]:
(16)
H
syll
= 8.6 bits/syllable
The average number of letters per syllable is 3.03, so that
(17)
H
3
= 8.6/3.03 = 2.84 bits/letter.
W. Fucks [F9] investigated the number of syllables per word, and found interesting frequency distributions which determine characteristic values for different languages.
The average number of syllables per word is illustrated in Figure 36 for some languages. These frequency distributions were obtained from fiction texts. We may find small differences in various books, but the overall result does not change. In English, 71.5% of all words are monosyllabic, 19.4% are bisyllabic, 6.8% consist of three syllables, 1.6% have four, etc. The respective values for German are 55.6%, 30.8%, 9.38%, 3.35%, 0.71%, 0.14%, 0.2%, and 0.01%.
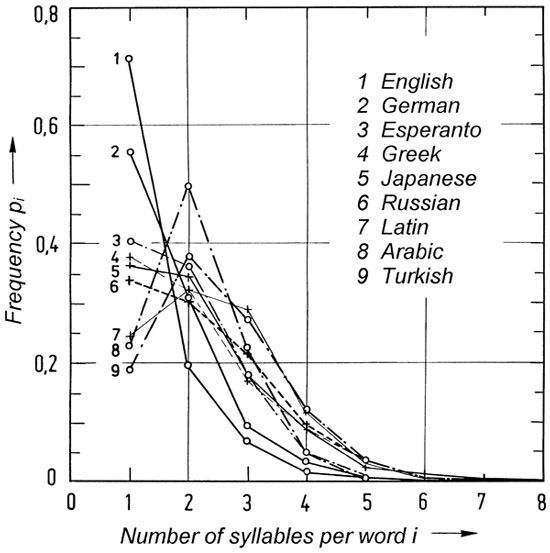 |
Figure 36: |