In the Beginning Was Information (27 page)
Read In the Beginning Was Information Online
Authors: Werner Gitt
Tags: #RELIGION / Religion & Science, #SCIENCE / Study & Teaching

For English, German, and Greek, the frequency distribution peaks at one syllable, but the modus for Arabic, Latin, and Turkish is two syllables (Figure 36). In Figure 37, the entropy
H
S
H
syllable
is plotted against the average number of syllables per word for various languages. Of the investigated languages, English has the smallest number of syllables per word, namely 1.4064, followed by German (1.634), Esperanto (1.895), Arabic (2.1036), Greek (2.1053), etc. The average ordinate values for syllable entropy
H
syllable
of the different languages have been found by means of equation (9), but it should be noted that the probabilities of occurrence of monosyllabic, bisyllabic, etc. words were used for p
i
. The value of
H
syllable
= 1.51 found for German, should not be compared with the value derived from equation (16), because a different method of computation is used.
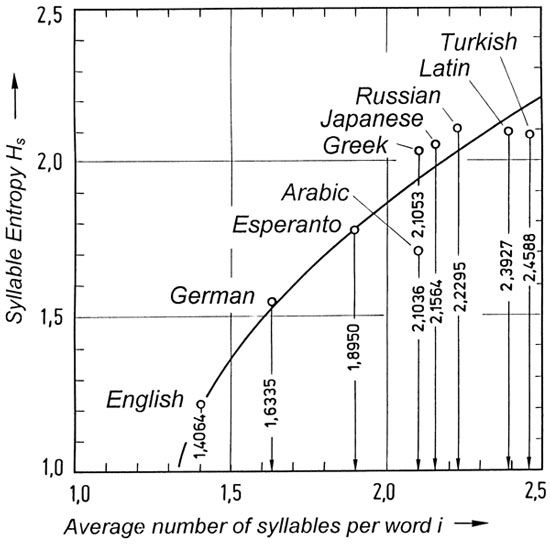 |
Figure 37: |
3. Words:
Statistical investigations of German showed that half of all written text comprises only 322 words [K4]. Using these words, it follows from equation (9) that the word entropy,
H
word
= 4.5 bits/word. When only the 16 most frequently used words, which already make up 20% of a text, are considered,
H
word
is found to be 1.237 bits per word. When all words are considered, we obtain the estimated 1.6 bits per letter, as indicated in equation (14). The average length of German words is 5.53 letters, so that the average information content is 5.53 x 1.6 = 8.85 bits per word.
It should now be clear that certain characteristics of a language may be described in terms of values derived from Shannon’s theory of information. These values are purely of a statistical nature, and do not tell us anything about the grammar of the language or the contents of a text. Just as the effective current
I
eff
of a continually changing electrical input (e.g., as a control parameter in a complex technological experiment) could be calculated as a statistical characteristic, it is also possible to establish analogous linguistic properties for languages. Just as
I
eff
can say nothing about the underlying control concepts, so such linguistic characteristics have no semantic relevance.
A1.5 Statistical Synthesis of Language
After having considered statistical analyses of languages in the previous section, the question now arises whether it would be possible to generate, by purely random combinations of symbols:
a) correct sentences in a given language
b) information (in the fullest sense of the concept)
Our point of departure is Figure 38. Random sequences of symbols can be obtained by means of computer program (1). When the letters may occur with equal frequency, then sequences of letters (output A in Figure 38) are obtained which do not at all reflect the simplest statistical characteristics of German or English or any other language. Seen statistically, we would never obtain a text which would even approximately resemble the morphological properties of a given language.
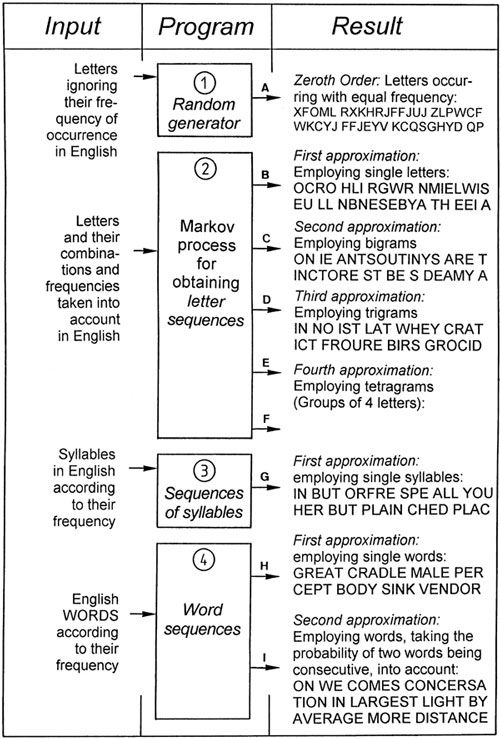 |
Figure 38: |
One can go a step further by writing a program (2), which takes the actual frequency of letter combinations of a language into consideration (German in this case). It may happen that the statistical links between successive letters are ignored, so that we would have a first order approximation. Karl Küpfmüller’s [K4] example of such a sequence is given as output B, but no known word is generated. If we now ensure that the probabilities of links between successive letters are also accounted for, outputs C, D, and E are obtained. Such sequences can be found by means of stochastic Markov processes, and are called Markov chains.
Program (2) requires extensive inputs which take all the groups of letters (bigrams, trigrams, etc.) appearing in Table 4 into account, as well as their probability of occurrence in German. With increased ordering, synthetic words arise, some of which can be recognized as German words, but structures like "gelijkwaardig," "ryljetek," and "fortuitousness" are increasingly precluded by the programming. What is more, only a subset of the morphologically typical German sounding groups like WONDINGLIN, ISAR, ANORER, GAN, STEHEN, and DISPONIN are actual German words. Even in the case of the higher degree approximations one cannot prevent the generation of words which do not exist at all in speech usage.
A next step would be program (3) where
only actual German syllables
and their frequency of occurrence are employed. Then, in conclusion, program (4) prevents the generation of groups of letters which do not occur in German. Such a program requires a complete dictionary to be stored, and word frequencies are also taken into account (first approximation). As a second approximation, the probability of one word following another is also considered. It should be noted that the programs involved, as well as the voluminous data requirements, comprise many ideas, but even so, the results are just as meager as they are unambiguous: In all these cases we obtain "texts" which may be morphologically correct, but are semantic nonsense.
A word is not merely a sequence of letters, but it has a nomenclatorial function which refers to a specific object (e.g., Richard the Lion Heart, Matterhorn, or London) or a class of objects (animal, car, or church) according to the conventions of the language. Every language has its own naming conventions for the same object, as for example "HOUSE," German "HAUS," Spanish "CASA," French "MAISON," and Finnish "TALON." In addition, a single word also has a meaning in the narrow sense of the word.
On the other hand, a sentence describes a situation, a condition, or an event, i.e., a sentence has an overall meaning. It consists of various single words, but the meaning of a sentence comprises more than just a sequential chain of the meanings of the words. The relationships between the sense of a sentence and the meanings of the words it contains are a semantic problem which can only be investigated in the framework of the delicately shaded meanings of the language conventions existing between the sender and the recipient of the message.
Conclusion:
Even though complete sets of letter groups, syllables, and words are used, together with their previously established frequency distributions, the statistically produced texts generated by various programming systems lack the decisive criteria which would ensure that a sequence of letters comprises a real message. The following criteria have to be met before a sequence of symbols can be accorded the status of information (a message):
1. Meaning accorded by the sender:
A set of symbols must have been transmitted by a sender and must be directed at a recipient. (If the described process did generate a letter sequence like "I LOVE YOU," I would be able to understand the text, but it still is not information as far as I am concerned, because it was not transmitted by somebody who loves me.)
2. Truth based in reality:
The set of symbols must contain actual truth pertaining to the real world. (If a statistical process might produce a sentence like "PARIS IS THE CAPITAL OF FRANCE," this is correct and true, but it has no practical significance, because it is not rooted in a real experience.)
3. Recognizable intention:
A sequence of symbols must be purposefully intentional, i.e., it must have been conceptualized by a sender.
4. Oriented toward a recipient:
The sequence of symbols must be addressed to or directed at somebody. (When a letter or a telegram is dispatched, the sender has a very definite recipient in mind; a book has a certain specific readership; when a bee performs a food dance, important information is conveyed to the other bees in the hive; DNA information is transferred to RNA which then leads to protein synthesis.) Recipient orientation is also involved even when there is a captive audience in addition to the intended recipient (e.g., unintentional listening in to a conversation in a train compartment).
Theorem A2:
Random letter sequences or sequences produced by statistical processes do not comprise information. Even if the information content could be calculated according to Shannon’s theory, the real nature of information is still ignored.
In the historical debate in Oxford in 1860 between Samuel Wilberforce (1805–1873) and the Darwinist Thomas H. Huxley (1825–1895), the latter stated that if monkeys should strum typewriters randomly for a long enough time, then Psalm 23 would emerge sooner or later. Huxley used this argument to demonstrate that life could have originated by chance, but this question is easily resolved by means of the information theorems. It follows from the theorems mentioned in chapter 4 and from Theorem A2 that information is not at all involved. The comparison invoked by Huxley has no bearing on information nor on life. The properties of information discussed in chapter 5, show that Huxley spoke about random sequences, but information was not involved in this argument about monkeys typing. It is impossible for information to originate in matter by random processes (see Theorem 1).
Questions a) and b) raised above, can now be answered unambiguously:
– It is only possible to synthesize, by means of a statistical process, correct sentences obeying the conventions of a given language, if the required know-how is included beforehand in the data (valid morphemes, syllables, and words) and in the programs. These programs require enormous efforts, and it is then even possible to generate sentences which obey the syntactical rules of the language. Even if some meaning could be ascribed to a sequence of words obtained in this way, it can still not be regarded as having "message quality," because it originated in a random process.
– Statistical processes cannot generate real information or real messages.
Appendix A2
Language: The Medium for Creating, Communicating, and Storing Information
A2.1 Natural Languages
Man’s natural language is the most comprehensive as well as the most differentiated means of expression. This special gift has been given to human beings only, allowing us to express all our feelings and our deepest beliefs, as well as to describe the interrelationships prevailing in nature, in life, and in the field of technology. Language is the calculus required for formulating all kinds of thoughts; it is also essential for conveying information. We will now investigate this uniquely human phenomenon. First of all, some definitions of language are given, and it should be clear that a brief definition is not possible as is the case for information [L3, p. 13–17]:
Definition L1:
Language is an exclusively human method for communicating thoughts, feelings, and wishes; it is not rooted in instinct, and it employs a system of freely structured symbols (Spair).