Life's Ratchet: How Molecular Machines Extract Order from Chaos (23 page)

J
AMES CLERK MAXWELL (1831–1879) LEFT BEHIND A distinguished scientific legacy. He unified electricity and magnetism, discovered electromagnetic waves and explained the nature of light, solved the riddle of Saturn’s rings, developed modern color theory, laid the foundations for engineering control theory, and cofounded statistical mechanics. In addition to all this, he invented a demon.

The Scottish physicist’s work on thermodynamics and statistical physics,
The Theory of Heat
, remains an example of clarity. Describing the second law of thermodynamics, Maxwell wrote: “One of the best established facts in thermodynamics is that it is impossible in a [closed] system . . . which permits neither change of volume nor passage of heat, and in which both the temperature and the pressure are everywhere the same, to produce any inequality of temperature or pressure without the expenditure of work. This is the second law of thermodynamics, and it is undoubtedly true as long as we can deal with bodies only in mass, and have no power of perceiving or handling the separate molecules of which they are made up.”

This quote presents as clear a definition of the second law as we could hope for. The law forbids the creation of temperature or pressure differences in a uniform medium, unless work is expended to create the difference. Yet at the end of the quote, Maxwell included a caveat: As long as we deal with many molecules (“in mass”) and have no way to look at them individually, the second law is true. But what if we
could
look at molecules individually? Maxwell continued: “But if we conceive a being whose faculties are so sharpened that he can follow every molecule in its course, such a being, whose attributes are still as essentially finite as our own, would be able to do what is presently impossible to us.” Could such a being violate the second law?

The second law was invented to explain certain limitations of machines: It was well known that steam engines wasted a lot of energy—most of the energy supplied in the form of coal was wasted as heat and not turned into mechanical work. Physicists and engineers from the late 1700s to the mid 1800s were preoccupied with improving the efficiency of engines. The efficiency is the ratio of useful energy generated to the energy input in the form of fuel. For example, a car engine has an efficiency of about 25 percent. Only 25 percent of the gasoline we put into the tank is used for moving the car or running the electrical systems; the rest is lost as heat. Is there a limit to the efficiency of engines? Could a 100 percent efficient engine be made, at least in principle?

The new science of thermodynamics, and the understanding that heat was a form of energy, led Helmholtz to his universal law of energy conservation.
Helmholtz convincingly demonstrated that motion and growth of a living being had to be powered by chemical fuel—food. In this sense, a living organism was similar to an engine. Like an engine, it converted a high-quality form of energy to both motion and heat. Again the question arose: Was there a limit to the efficiency of life’s engines?

By the beginning of the twentieth century, it was becoming clear that the engines of life operated at the molecular scale. How can we understand such machines, and how does their operation relate to the macroscopic machines of our everyday experience?

Macroscopic machines—car engines, power plants, etc.—exploit
gradients
, that is, differences in temperature or pressure, to convert fuel into motion. This important observation was first made by a young French military engineer, Sadi Carnot (1796–1832), in 1824. Carnot laid the groundwork for modern thermodynamics when he realized that the efficiency of engines could not be increased to 100 percent, even in principle, but instead was limited by the temperature gradient they exploited. In other words, the hotter the fire, and the colder the surroundings, the more efficient a machine could become. When the inside of an engine approaches the temperature of the surroundings, no more work can be done by the engine, and the efficiency goes to zero. We then have the situation Maxwell described in his definition of the second law.

In living cells, temperatures and pressures are uniform—there is no combustion chamber or pressure reservoir. There are no temperature or pressure gradients. According to Carnot, no engine should be able to operate in our bodies. The second law of thermodynamics allows us to extract work from gradients, at the cost of creating waste heat and the leveling of the gradient. The result is equilibrium—a state of uniform temperature and pressure, a state from which no further work can be extracted. How can molecular machines extract work from the uniform-temperature environment of cells without violating the second law of thermodynamics?

When the second law was formulated in the nineteenth century, physicists were not certain if it was an incontrovertible law of nature. What was the basis of this law? Physicists like to employ many methods to get to the bottom of things: experiments, theoretical calculations, and gedankenexperiments.
Gedankenexperiment
is a German word, sometimes used in English, meaning “thought experiment.” It is a hypothetical situation,
which can only exist in thought and is a stress test for physics theories. The idea is either to create a paradox—a contradiction between different physical theories—or to see how far you can stretch a theory or an experimental result into a realm that is inaccessible to the real world. Famous thought experiments include Schrödinger’s cat (which showed the absurdity of some interpretations of quantum mechanics); Galileo’s deduction of constant acceleration during free fall, irrespective of the mass of the falling object (Galileo never threw objects off the Tower of Pisa—he inferred what would happen from rolling balls down inclines); Newton’s cannonball (which showed that the motion of celestial objects is related to the falling of objects on Earth); and Maxwell’s demon, the little creature who could transfer heat from cold to hot.

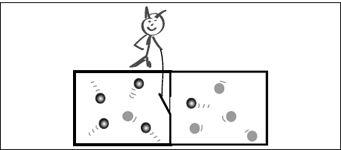
FIGURE 5.1.
Maxwell’s demon sorts fast-moving molecules into the left chamber and slow ones into the right chamber by controlling a small trap door. After a while, he succeeds in creating a temperature difference between the chambers without expending work, thus seemingly violating the second law.

Maxwell’s demon, which he devised in 1867, was a tiny hypothetical creature who controlled a little door separating two gas-filled chambers, which initially have the same average temperature (
Figure 5.1
). The job of the demon was to separate gas molecules into fast and slow molecules. If, for example, a fast molecule approached the demon’s door from the right, the demon would let it through the door to the left chamber, but if it was slow, he would not. Conversely, he was happy to let slow molecules pass from the left to the right chamber, but not fast ones. Soon, the demon had sorted fast molecules into the left chamber, while leaving all the slow ones in the right chamber. Starting from a uniform-temperature system, the demon had created a temperature gradient—making one side cold
and the other side hot (remember that the temperature of a gas is directly related to the speed of the gas molecules). This temperature gradient could now be used to do work if a little turbine were placed into the demon’s door. The result would be to extract useful work from a uniform-temperature system, in clear contradiction of the second law. On the other hand, such a molecular Maxwell demon would be just what is needed to explain molecular machines! Are our cells full of molecular Maxwell demons? Does life, deep down, violate the second law?

Marian von Smoluchowski (1872–1917) spent a great deal of time thinking about the second law. An avid mountain climber, the Polish-Austrian physicist wrote prodigiously about everything, from the folding of mountains and erosion by glaciers to diffusion in colloids and heat transfer in liquids. He published his explanation of Brownian motion almost simultaneously with Albert Einstein, although he later admitted that Einstein’s solution had the correct prefactor, and his didn’t.

One of his many papers, “Experimentally Demonstrable Molecular Phenomena, Which Contradict Standard Thermodynamics,” was published in 1912. In this paper, he discussed special states of matter where fluctuations—spontaneous deviations from the average value of some property (pressure or density, for example)—suddenly become very large. This happens for some gases close to a phase transformation. Smoluchowski asked, What if we could use these pressure fluctuations to push a one-way door? When the pressure gets high enough, the door will open; when it is too low, the door will remain closed. This would be an automated Maxwell demon: Smoluchowski’s trap door would only let high-velocity (high-pressure) molecules through, while rejecting low-velocity molecules. According to Smoluchowski, several physicists of the age considered such hypothetical contraptions a serious objection to the second law. But Smoluchowski dismissed this idea. The problem, according to him, was in how strong the door was. If the door was very weak, or easy to open, it would be subject to thermal motion and would randomly open by itself—letting slow molecules through when it shouldn’t, or letting fast molecules escape back into the slow pool. If the door could be made strong
enough to avoid this problem, it might not open at all. And for values in between? The door would be unreliable. Sometimes it would not open when it should, and sometimes it would open when it shouldn’t. Smoluchowski did not present a rigorous calculation in this paper, but he asserted that such a trap door would never work. The second law could not be violated using an automated trap door.

Toward the end of the paper, Smoluchowski emphatically pointed out that the second law
could
be violated—if we were willing to wait long enough. This is charmingly illustrated in physicist George Gamow’s series of novels in which the hero, bank clerk Mr. Tompkins, learns about physics. In one book, Maxwell’s demon makes Mr. Tompkins’s highball boil, which prompts Mr. Tompkins’s friend, the “professor,” to excitedly exclaim how lucky they are: “In the billions of years to come, we will still, probably, be the only people who ever had the chance to observe this extraordinary phenomenon!” The second law is a statistical law—which states that
most of the time
(usually very close to “always”), systems tend toward their most probable state. However, if we are willing to wait long enough, strange things can happen by chance. I could win a million in roulette. Your cold coffee could spontaneously boil. But we’d be waiting a very, very long time for these things to happen.

How long? The waiting time depends on the probability, which in turn depends on the size of the system. In a large system, one visible with an optical microscope or larger, a violation of the second law will, for all practical purposes, never happen. However, a really small system (a single molecule, for example) can seemingly violate the second law relatively often. This was Maxwell’s point when he invented the demon. Maxwell was not out to disprove the second law. He simply wanted to show that the second law
emerges
once we talk about a large number of molecules. It is a statistical law. This is why we usually do not apply the second law to single molecules.

Smoluchowski went on to point out that even though a small system may be able to violate the second law once, you cannot build, from such a small system, a device that can act like Maxwell’s demon. The reason is that violating the second law happens randomly and not
repeatedly
. Consequently, the second law should be stated this way: You cannot
repeatedly
extract energy from a uniform heat bath.

But if it could happen once, why not repeatedly? Let’s look at why not.

Maxwell’s demon has been giving physicists a headache for a long time. Although Maxwell invented the little creature to show that the second law was only a statistical law, physicists later saw it as a serious assault on the law itself. In the interest of professional pride, the demon had to be exorcised.

Several solutions were proposed. One solution, proposed by the physicists Leo Szilard (1898–1964) and Leon Brillouin (1889–1969), posited that the very act of measuring the speeds of molecules would necessarily involve some energy, which would be dissipated. For example, the demon could try to measure the molecular speed with light pulses—but not all the light energy would be recoverable. The dissipated energy would lead to an increase in entropy larger than the decrease in entropy from the sorting of the molecules. However, more recently, computer scientists Rolf Landauer (1927–1999) and Charles Bennett (b. 1943) have pointed out that the measurement
could
be done without energy loss or entropy increase. Instead, the entropy increase would occur when the demon erases his short-term memory to make room for the next measurement. This solution to the demon conundrum created an intriguing connection between entropy and information storage, which is still a hot topic today.