Más rápido que la velocidad de la luz (36 page)
Read Más rápido que la velocidad de la luz Online
Authors: João Magueijo
Tags: #divulgación científica

Nuestra labor descansaba en una premisa desconcertante por su sencillez. Sabíamos que la teoría cuántica de la gravedad habría de vaticinar fenómenos nuevos, pero, contra la tónica general, fuimos modestos y supusimos que con la tecnología actual no habría manera de comprobar esos efectos. Teníamos una única certeza: con las energías miserablemente bajas que aportaban los aceleradores o en las enormes escalas temporales en que nuestros sensores pueden detectar la curvatura,
no
se han podido observar efectos gravitatorios cuánticos y lo menos que se puede decir es que la gravedad clásica (es decir, la teoría general de la relatividad) es una excelente aproximación al mundo real.

Lee Smolin
Nuestro único supuesto, entonces, fue postular la existencia de un
umbral
, por encima del cual se volverían significativos nuevos efectos correspondientes a la gravedad cuántica, y por debajo del cual esos efectos serían despreciables. Ese umbral estaría caracterizado por un nivel de energía, denominada energía de Planck (E
p
), y los efectos nuevos sólo aparecerían por encima de ella. Análogamente, debería existir una longitud, la longitud de Planck (L
p
), que indicaría qué ampliación sería necesaria en un "microscopio" gravitato-rio cuántico para que se pudiera ver la naturaleza discreta del espacio y de la curvatura. Por último, debería existir también una duración, el tiempo de Planck (t
p
), que indicaría la breve vida de esos efectos.
De hecho, no necesitábamos conocer el valor concreto de E
p
, L
p
ni t
p
: sólo necesitábamos saber que debía
existir
un umbral, por debajo del cual las cosas serían más o menos las mismas de siempre, y por encima del cual entraríamos en un mundo nuevo y desconocido aún para nosotros, en cuyo ámbito la gravedad sería cuántica y se unificarían todas las fuerzas y partículas de la naturaleza.
Era un supuesto razonable. La relatividad general se reduce a la gravedad newtoniana siempre que la intensidad gravitatoria no sea excesiva. Análogamente, cualquiera sea la forma que adopte en definitiva la gravedad cuántica, deberá empezar por confirmar y reiterar todo lo que han dicho anteriormente los maestros, es decir, no será distinguible de las teorías actuales en una primera aproximación y sólo habrá predicciones nuevas en condiciones muy extremas: a energías muy altas o a distancias y períodos muy cortos. A fin de cuentas, se trata de una restricción de las observaciones.
Llegados a este punto, advertimos una contradicción. Supongamos que un granjero ve una vaca pastando en el campo. Puesto que la vaca es mucho más grande que L , el granjero no tiene por qué preocuparse por los efectos de la gravedad cuántica. Pero en ese momento, la eterna Cornelia pasa a su lado en una de sus locas carreras a una velocidad muy próxima a la de la luz, pero lo que ella ve es distinto: con respecto a ella, la vaca que pasta se mueve a mucha velocidad, de modo que Cornelia ve su tamaño reducido en la dirección del movimiento, tal como predice la relatividad especial. Si su velocidad es suficientemente grande, Cornelia verá el tamaño de la otra vaca tan reducido que su longitud será menor que L , y llegará a la conclusión de que sufre un ataque de fiebre gravitatoria cuántica, si es que eso existe. No sería sorprendente que viera que la apacible vaca hace una exhibición de zapateo americano, que inicia una danza erótica o que se comporta de acuerdo con los desconocidos efectos que la gravedad cuántica produce sobre las vacas.
Sin embargo, puesto que la vaca que pasta en el prado es una entidad única, todo lo que haga debería ser previsible según una misma teoría. El requisito mínimo para la unificación sería que todos los observadores usaran una misma teoría. En otras palabras, es inadmisible una situación en la que el granjero y Cornelia tuvieran que aplicar distintas teorías para describir el mismo objeto: hacerlo sería un insulto a la unificación y totalmente incompatible con el principio de relatividad. Si, en efecto, el movimiento es relativo, Cornelia no puede saber que ella se está moviendo y que el granjero está quieto.
Una vez más, Cornelia y el granjero están en desacuerdo, pero esta vez no coinciden sobre la frontera que separa la gravedad clásica de la cuántica.
Surgen paradojas similares si definimos el umbral mediante la longitud de Planck, la energía de Planck o el tiempo de Planck. Por ejemplo, si uno recurre al lenguaje de la energía, el problema se plantea en el corazón mismo de la fórmula más famosa de la física, E = mc
2
. Como ya hemos visto, las partículas en movimiento tienen una masa mayor, razón por la cual no es posible acelerar ningún objeto más allá de la velocidad de la luz. Por consiguiente, para el granjero, un electrón estacionario es una partícula hecha y derecha, pues su energía es mucho menor que E ; sin embargo, para Cornelia, el electrón tiene una energía mucho mayor porque está en movimiento con respecto a ella y tiene por ende una masa más grande. De modo que ella aplica la fórmula E = mc
2
y llega a la conclusión de que esa masa implica una energía mayor. Si la velocidad de Cornelia es suficientemente alta, observará que el electrón tiene una energía mucho mayor que E e inferirá de ese hecho que para el electrón rigen los efectos de la gravedad cuántica. Una vez más, hay contradicción.
Lee y yo analizamos estas paradojas durante meses a partir de enero de 2001. Nos encontrábamos en bares de South Kensington o Holland Park para reflexionar sobre el problema. Evidentemente, las dificultades radicaban en la relatividad especial, pues todas las paradojas surgían de los consabidos efectos relativistas, como la contracción de la longitud, la dilatación del tiempo o la fórmula E = mc
2
. La situación impedía definir una frontera nítida, común a todos los observadores, que pudiera englobar los nuevos efectos gravitatorios cuánticos. Parecía que no había un dique que pudiera contener la gravedad cuántica: sus efectos se derramaban por todas partes a consecuencia de la relatividad especial subyacente.
La conclusión era inevitable: para elaborar una teoría cuántica de la gravedad,
cualquier
cosa que ella fuese, sería necesario dejar de lado la relatividad especial. Nos dimos cuenta de que muchas de las incoherencias que afectaban las teorías gravitatorias cuánticas propuestas hasta entonces provenían probablemente de aceptar religiosamente la relatividad especial. Razonamos entonces que, antes que nada, había que sustituir la relatividad especial por algo que permitiera que por lo menos uno de los tres umbrales —E
p
, L
p
o t
p
— fuera idéntico para todos los observadores. Nada que fuera más grande que L debía contraerse por obra del movimiento hasta convertirse en algo más pequeño que L . Podía ocurrir que las partículas tuvieran mayor masa si estaban en movimiento, pero si su energía en reposo era menor que E , debía continuar siéndolo, por veloz que fuera su movimiento observado. Una vez alcanzado el umbral E (o L ), todos los efectos relativistas deberían interrumpirse y esos valores deberían adquirir carácter absoluto. Tales eran los requisitos de la nueva teoría.
Lo difícil era construir una teoría que los satisficiera. Sólo algo era evidente: cualquier cosa que elaboráramos entraría en conflicto con la relatividad especial. Como se vio anteriormente, la relatividad especial descansa en dos principios independientes: la relatividad del movimiento y la constancia de la velocidad de la luz. Así, pues, una solución consistía en abandonar el principio de relatividad del movimiento suponiendo que a velocidades muy grandes los observadores advertirán que su movimiento es absoluto. Sentirán entonces una especie de brisa del éter y Cornelia se dará cuenta por fin de que el granjero está en reposo mientras ella se desplaza en un vuelo enloquecido.
Era una posibilidad, pero decidimos adoptar la otra: quedarnos con la relatividad del movimiento pero admitir que, a energías muy altas, la velocidad de la luz no es constante. Ahí entraba la velocidad variable de la luz en la argumentación.
Hicimos modificaciones mínimas a la relatividad especial y pronto estuvimos en condiciones de deducir las ecuaciones equivalentes a las transformaciones de Lorentz para nuestra teoría. Nos divertimos mucho haciendo esos cálculos. Las nuevas ecuaciones eran bastante más complejas (no eran lineales), pero se atenían dentro de lo posible a la relatividad especial y general. Según ellas, a medida que nos acercáramos a L
p
o a t
p
, el espacio y el tiempo serían cada vez menos flexibles, como si la velocidad de la luz creciera cada vez más a medida que uno se aproxima a la frontera entre la gravedad clásica y la cuántica. En la frontera, parecería que la velocidad de la luz se hace infinita, y el espacio y el tiempo volverían a ser absolutos, aunque no en general sino para una longitud y un tiempo determinados —L
p
y t
p
—, de modo que todos podían ponerse de acuerdo sobre qué ámbito correspondía a la gravedad clásica y cuál era del dominio de la gravedad cuántica. Así, la teoría trazaba una nítida línea divisoria entre esos dos reinos.
La famosa ecuación de Einstein, E = mc
2
, se ha transformado a tal punto en una especie de símbolo sagrado, que se apoderó de mí un gran placer iconoclasta cuando desarrollábamos la teoría alternativa. En consecuencia, y aunque signifique un exceso de matemáticas para un libro de esta índole, me veo obligado a transcribir la fórmula aquí. Ruego al lector que me tenga paciencia y le eche un vistazo:
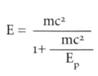
(En esta fórmula c representa aproximadamente el valor constante de la velocidad de la luz que medimos cuando las energías son bajas.) Tengo perfecta conciencia de que esta fórmula no es comparable en belleza con la de Einstein, pero cualquiera que conozca algo de matemáticas advertirá que de ella se infiere de inmediato una propiedad notable. Cuando Cornelia pasa a toda velocidad, si ésta es suficientemente grande, para ella un electrón en reposo que está en la granja podrá tener una masa enorme. Según la ecuación habitual E = mc
2
, ese hecho significa que la vaca puede observar que la energía del electrón es más grande que E , de modo que arribamos a la desconcertante conclusión de que no hay acuerdo entre ella y el granjero respecto de que una teoría cuántica de la gravedad sea necesaria o no para comprender lo que ocurre con el electrón.
Con la nueva fórmula, ¡esa discrepancia desaparece! Si bien para Cornelia no hay un tope para m, una simple reflexión matemática indica que, según esta fórmula, la energía E del electrón jamás puede ser mayor que E . Por consiguiente, el granjero y la vaca concuerdan en que en el caso de ese electrón no hay un comportamiento gravitatorio cuántico.
Durante la Guerra Fría, cada vez que un físico descubría efectos nuevos, se apresuraba a investigar sus posibles aplicaciones militares, especialmente en los Estados Unidos. Neil Turok me contó que había cenado una vez durante un congreso con el famoso físico Edward Teller y que, en el curso de la conversación, le dijo que estaba trabajando en los monopolos magnéticos. Ante el verdadero espanto de Neil, el anciano empezó de inmediato a calcular cuánta energía podría generar una bomba construida a partir de ese principio.
Desde ya, hoy en día esas actitudes provocan risa, pero por el mero placer de tomarle el pelo a Lee, calculé la energía que podría liberar una bomba gravitatoria cuántica según nuestra fórmula. Es decir, que proponía averiguar cuánta riqueza ocultaba el hombre rico de la metáfora.
Supongamos que poderosísimos aceleradores pudieran producir una gran cantidad de partículas con la masa de Planck y que, de alguna manera, se fabricara con ellas una bomba. Según la teoría, semejante bomba liberaría exactamente
la mitad
de energía que libera un arma nuclear común de la misma masa. En otras palabras, esa carísima arma gravitatoria cuántica tendría la mitad del poder destructor que un arma nuclear clásica mucho más barata. En el caso de partículas con una masa mayor (por ejemplo, igual al doble o el triple de la masa de Planck), el resultado sería aún peor. Me alegró descubrir que ni siquiera un general podía ser tan necio como para contratarnos
[65]
.
Cuando todo este trabajo tan interesante estaba ya cobrando forma, en el verano de 2001, ¿adivine el lector qué sucedió? ¡Pues que Lee se fue del Imperial College! ¿Algún funcionario de esa institución percibe en ese hecho una especie de repetición? ¿O tal vez sea exigirles demasiado esfuerzo intelectual?