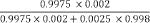Mathematics and the Real World (36 page)
Read Mathematics and the Real World Online
Authors: Zvi Artstein

Another aspect of Kolmogorov's axioms is that it gives a seal of approval to the use of the same mathematics for both types of probability, that is, probability in the sense of the frequency of the outcomes of many repeats, and the probability in the sense of assessing the likelihood of a non-repeated event. Both aspects of this duality are described by the same axioms. Indeed, another look at the three axioms above will show that common sense will accept both interpretations of probability. As the mathematics is based solely on the axioms, the same mathematics serves for both cases.
What then does assessing the probability of a non-repeated event mean? The mathematical answer is given in the axioms and their derivatives. The day-to-day implications are a matter of interpretation, which is likely to be subjective. It is interesting that late in life Kolmogorov himself expressed doubts about the interpretation of the probability theory related to non-repeated events, but he did not manage to propose another mathematical theory to be used to analyze this aspect of probability.
Kolmogorov's book changed the way mathematics dealt with randomness.
Concepts that had been considered just intuition became subject to clear mathematical definition and analysis, and theorems whose proofs had also relied on intuition were now proved rigorously. Within a short time Kolmogorov's model became the accepted model for the whole mathematical community. Nevertheless, as the reader who has not previously come across this mathematics can guess, the method Kolmogorov suggested was not easy to use. Moreover, the formalism failed to overcome the many difficulties and errors in the intuitive approach to randomness, because it is a logical formalism that the human brain is not set up to accept intuitively.
42. INTUITION VERSUS THE MATHEMATICS OF RANDOMNESS
When we react to a situation involving random events we use intuition that the human race developed over millions of years of evolution. As we claimed in the
first chapter
of this book, evolution did not provide us with the tools to think intuitively about situations involving logic. It is not just the difficulty in using an intuitive assessment of a situation in which logical consideration is the correct device to use; the naive use of intuition can lead to errors and even mental illusions similar to the visual illusions we examined in section 8. In this and the next section, we will analyze some of the common errors and illusions related to randomness.
We will start with a real-life example. Every blood donation is of course tested to ensure that the donor is not suffering from the HIV pathogen that causes AIDS. The error in the test is minimal, but it exists, and is about 0.25 percent. That means that there is a 99.75 percent chance that an HIV carrier will be correctly identified as such, but there is a quarter of one percent chance that the test will yield an incorrect result and the carrier will in error be declared healthy. There is an equal chance of a quarter of one percent that a perfectly healthy person will be incorrectly diagnosed as being an HIV carrier. A potential donor in a blood donation unit was tested, and the result showed him to be an HIV carrier. What is the chance that he really is a carrier?
The great majority of respondents answering that question (and I have asked it in different forums and of various audiences) assess that the chance that the person tested is a carrier is 99.75 percent, that is, in accordance with the possible error in the performance of the test. Few assess the chance as slightly smaller, generally without explaining why their assessment is lower than the figure we have set as the error. They presumably think that the correct answer is not 99.75 percent, otherwise why would they be asked such an apparently simple question? Very few give the right answer (and in general they have come across this or a similar question previously). What is the right answer? To arrive at the correct answer we must first examine what situations could have yielded a positive result in the test. The subject may indeed be an HIV carrier, and the chance of the test giving a positive result is very high, 99.75 percent. The subject may, however, be completely healthy, and the chance of the test giving an incorrect positive result is very small, 0.25 percent. Yet the population of healthy people is large compared with the population of HIV carriers, and the number of those whom the test wrongly identifies as carriers could be very large, larger than the entire population of actual carriers. In order to be able to assess the chances that the subject really is a carrier, we need to know one additional fact, and that is the proportion of carriers in the whole population. The figures published by the World Health Organization (WHO) show that in the developed countries HIV carriers constitute about 0.2 percent of the population, that is, one carrier per five hundred people. If we accept that figure, we can use Bayes's formula as described in the previous section. The formula weights the chances that a carrier will be identified as such in the test, compared with the chance that anyone, healthy or a carrier, will be found to be a carrier in the test. The calculation is
giving a probability of about 0.44, that is, the chance is only 44 percent that a positive result correctly identifies a carrier. If carriers were only 0.1 percent of the population, the chances fall to about 28.5 percent.
The fact that a donor's blood sample is tested, in other words the subject, that is, the donor, is chosen almost randomly, is an important fact of the analysis (it pertains to the assumption we made when introducing the formula in the previous section). If the subject had been sent for the test because he was suspected of being an HIV carrier, for example because he showed certain symptoms, the probability that he was really a carrier would be different; to find it we should use the original Bayes's scheme.
Why do most people asked the question consider that the chances that someone who gets a positive result in the test (as a carrier) really is a carrier is 99.75 percent? The reason lies in the way the brain analyzes the situation, a way that is inconsistent with the mathematical logical understanding of it. The brain perceives certain data and decides intuitively which are important, without undertaking an orderly analysis of the information. It does not look for missing information. Evolution instilled in us, or more precisely instilled in our subconscious minds, the recognition that it is generally not worthwhile to devote the effort necessary for a rigorous analysis of the problem. Therefore the brain concentrates on one prominent piece of information: the chance of an error is only a quarter of one percent.
This type of error is not confined to medical tests. Courts tend to convict someone who confesses to murder even without corroborating evidence. The reason that judges give is that the probability that someone will confess to a murder he has not committed is negligible. That fact is correct, but the statistical conclusion is not. To illustrate: assume that only one person in one hundred thousand will confess to a murder he has not committed (and taking into account the conditions of police interrogation that suspects undergo, that assumption is certainly not an overestimate). Assume also that someone is arrested randomly from a population of four hundred thousand, and he confesses to a murder committed the previous day. The chance that he is the real murderer is only 20 percent! The chance that the real murderer was found is only one in five (the murderer himself, if he confesses, and the other four of the population who would confess even if they have not committed the murder). With a larger population, the chances are even lower. The mistake the judges make lies in the fact that
they only examine the chances that someone has been arrested who has a tendency to admit to a crime he did not commit; but once the suspect confesses, that probability has no significance. Once a suspect has confessed, what matters is how to differentiate between those who would make a false confession and the real murderer. That can be done by means of additional evidence or suspicious circumstances. Judges often overlook this distinction. In an article published in the Israeli journal
Law Studies
(
Mechkarey Mishpat
) in 2010, Mordechai Halpert and Boaz Sangero analyze the case of Suliman Al-Abid, who confessed to the murder of a girl and was convicted despite the fact that there was hardly any independent circumstantial evidence implicating him. Eventually it was found that he had been convicted wrongly. The article discloses the error in probability made by the judges and brings other examples from the legal area.
As an introduction to the next example, here is an amusing anecdote. A man is caught at an airport trying to board a plane with a bomb in his suitcase. His argument was as follows: “I did not intend to blow up the plane, but I heard that the chances of two people who do not know each other both taking a bomb onto a plane is much smaller than the chances of one person trying to do so, so I took a bomb with me to reduce the chances that the plane will be blown up.” Clearly the logic employed by this passenger is flawed, but is it easy to pinpoint the mistake? Such errors occur, however, not as a joke, but in many situations we encounter in our daily lives. Here is another example.
This occurred in the trial of O. J. Simpson, the famous American football player accused of the murder of his ex-wife and her boyfriend. To support its case, the prosecution cited evidence that Simpson had beaten his ex-wife previously and had threatened several times that he would kill her. These instances had been brought to the attention of the police, and they had had to intervene on a number of occasions and remove him from her house. The defense brought the following probability counterargument. Reliable statistics covering thousands of cases showed that of those instances registered by the police, less than one-tenth of those who beat their spouses and threaten to kill them actually attempt to do so. Even
fewer, less than one in a hundred, actually kill their spouse. The conclusion to be drawn, according to the defense, is that the chances that O. J. Simpson actually killed his ex-wife are less than 1 percent, a probability that constitutes reasonable doubt. The jury apparently accepted that claim, and even the judge did not comment on the basic error made by the defense. The defendant was acquitted. A proper analysis shows that the probability calculation presented by the defense did not take into account a basic relevant fact: Mrs. Simpson
was
murdered. If that undeniable fact is taken into consideration and the question is then asked that if a woman has been threatened by her ex-husband and is then murdered, what are the chances that she was murdered by that ex-husband, the chances are very different from those presented by the defense. It would be wrong to conclude that the jurors were uneducated or ignorant. Evolution did not prepare us for proper analysis of issues in which the claims are logical arguments.
Here is another example that reflects a real-life situation. Six equally attractive girls reached the final round in a beauty contest. Each has the same chance of winning. The winner has been selected, but it has not been announced who it is, and the girls are on their way to the stage for the declaration of the winner. The last girl in line on the way to the stage, number six, cannot suppress her curiosity, and asks the guard, who knows who the winner is, to tell her. He answers that he is forbidden to reveal the result, but he does tell her that number one is not the winner. Number six is happy; her chances, she thinks, have just risen from a sixth to a fifth. Is she right? Most people asked the question answer that she is right, or they say that her chances remain as they were, one-sixth. The argument put forward by the first group is that five contestants are left, and the fact that number one is not the winner does not add any information about the others, so the remaining contestants’ chances are equal, that is, a fifth. The others argue that as the guard had to mention one contestant who had not won, the fact that he indicated one of those who had not won did not add any information, and the chances of the remaining contestants remained as they were, that is, one sixth. These are intuitive answers. Very few people notice that one vital piece of information is missing, without which no reliable answer can be given! The story does not reveal the method adopted by
the guard, that is, the algorithm or formula according to which he acted and that determined the
a priori
probabilities that he would indicate number one as a non-winner. Try to complete what is needed in Bayes's scheme, and you will see that there is insufficient information available for it to be used. Without information that details the possibilities in which the guard would point out the number one contestant as a non-successful participant, it is impossible to answer the question. It is easy to make up a story describing how the guard would behave so that the chances remain one-sixth (for instance, the guard chooses the girl he points out at random among those who have not won, excluding number six—we leave out the computation). But it is also possible to make up another story about his behavior that would increase the chances to one-fifth (for instance, the guard picks, among those who have not won, the one who gets on the podium first). It is even possible to depict other scenarios that will lead to other consequences. The human brain is not constructed in such a way that it searches for missing information. Such a search is wasteful from an evolutionary standpoint. The brain fills in what is missing from the story of the event with reasonable data. Sometimes this turns out to be correct, and sometimes not. This efficiency of the brain is justified in most day-to-day problems, but it is far from consistent with mathematical analysis.